螺栓组连接的受力分析及强度计算实例

【实例1】 如图1-10所示，一个厚度δ＝12mm的钢板用四个螺栓连接在厚度δ₁＝30mm的铸铁架上。螺栓的性能等级为4.6级，［τ］＝96MPa；铸铁架［σ_P1］＝180MPa，钢板［σ_P2］＝320MPa；螺栓为M16～M48，安全系数S_s＝2.5，板和架之间的摩擦因数_μs＝0.15；载荷F∑＝12kN；尺寸L＝400mm，a＝100mm。

1）图示螺栓布置。两种方案中哪一种合理些？

2）选择合理方案，采用普通螺栓连接和铰制孔光螺栓连接，哪一种连接合理些（为可靠起见，摩擦力加大20％）？

解：要分析两种方案哪一种合理些，就是要分析两种方案中，受力最大的螺栓受的力是多少，其受力越小的方案越合理。

图1-10 螺栓布置方案示意图

首先进行螺栓组的受力分析计算：将外载荷移到螺栓组接缝面的几何形心。如果每个螺栓所受的力都是横向力，则应该将这些横向力进行几何合成，求出每个螺栓所受的总的横向力。

1.螺栓组受力分析及计算

如图1-11所示，将载荷F_∑移至螺栓组形心O，得一横向力F_∑和旋转力矩：T＝F_∑l＝4800000N·mm。

2.求螺栓受的横向力

在横向力F_∑作用下各螺栓受横向力的方向与F_∑相同，即垂直向下，每个螺栓受的力为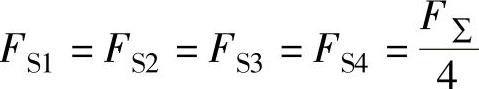，为了清晰，在图1-12中皆用符号F_S1表示。

图1-11 F∑平移后螺栓组连接的受力

在转矩T作用下，各螺栓受一横向力，方向各垂直于回转半径r_i；又因各螺栓中心距离螺栓组几何形心O的距离相等，所以各螺栓在转矩T作用下受的横向力也相等，为了清晰，在图1-12中皆用符号F_S2来表示。

图1-12 各螺栓的受力

方案一中，各螺栓距形心的距离为

在转矩T作用下各个螺栓受的横向力为

由图1-12a可知，螺栓1和2所受的力F_S1和F_S2之间的夹角α最小，故螺栓1、2受力最大，根据余弦定理可求出螺栓1或2所受总的横向力为

方案二中，r₁＝r₂＝r₃＝r₄＝r＝a＝100mm，故在扭转力矩T作用下各螺栓受的横向力相等：

由图可知，螺栓1和2所受的力F_S1和F_S2之间的夹角α最小（夹角为0），因此其合力最大，螺栓1所受横向力的合力为

F_Smax（2）＝F_S1＋F_S2＝3000N＋12000N＝15000N

3.两种方案比较

因方案一中受力最大的螺栓1、2所受的总横向力为F_Smax（1）＝10820N，而方案二中受力最大的螺栓1所受的总横向力为F_Smax（2）＝15000N，F_Smax（1）＜F_Smax（2），因此方案一比较合理。以下按方案一设计两种形式的连接，并进行比较。

4.受剪螺栓（或铰制孔光螺栓）连接的计算

按设计螺栓光杆部分直径：

查螺栓标准取M12，则d＝13mm。

验算抗压强度略。

5.受拉螺栓（普通螺栓）连接计算

横向力被接缝面之间的摩擦力平衡，从而求出预紧力，即，此处FS为受力最大的螺栓（方案一中螺栓1及2）受的总的横向力（前面所求F_S1和F_S2的矢量合成），所以公式中的Z＝1；只有一个接合面，故m＝1，预紧力为

由性能等级4.6级可得σ_S＝4×6×10MPa＝240MPa。已知安全系数S_S＝2.5，则有

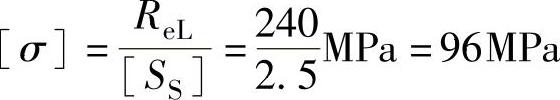
代入求出

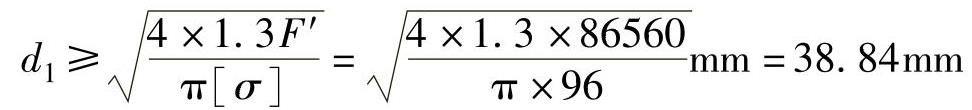
查螺纹标准，取M45的螺纹（根径d₁＝40.129mm）。

6.两种螺栓连接的比较

从以上的计算可知：在螺栓所受总的横向力一定的情况下，采用铰制孔光螺栓时，只需要M12的螺栓即可满足强度需要；而同样的横向力设计成受拉螺栓（普通螺栓）时，则需要M45的螺栓。从减小尺寸的角度考虑，采用铰制孔光螺栓连接更为合适。但采用铰制孔光螺栓时，对螺栓孔的加工精度要求较高，不仅需要钻孔，还需要铰孔，加工成本较高；而且铰制孔光螺栓也比普通螺栓的价格高。因此，应该根据使用要求决定采用螺栓的种类。

图1-13 方形盖板尺寸及受力

【实例2】 方形盖板用四个M16螺钉与箱体连接，于盖板中心O点装有吊环，已知Q＝20kN，尺寸如图1-13所示，取残余预紧力F″＝0.6F。

1）校核M16螺钉的强度，螺钉性能等级取6.8级，安全系数取4.3。

2）若由于制造误差，吊环由O点移至对角线上的O′点，且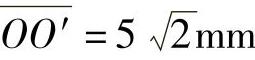，问哪个螺钉受力最大。试校核其强度。

解：

1）首先将外载荷移到螺栓组接缝面的几何形心，本题第一问中吊环中心就在几何形心O点。

此螺栓的受力属于既受预紧力又受工作载荷的情况，首先求出总拉力。由已知条件知，残余预紧力F″＝0.6F，代入下式：

F₀＝F″＋F＝0.6F＋F＝1.6F

工作载荷是由轴向力Q引起的，即

F＝Q／4＝20×10³N／4＝5000N

代入强度公式，尚需求出许用应力［σ］：螺钉的性能等级为6.8级时R_eL＝480MPa；已知安全系数［S_S］＝4.3，许用应力为

所以螺钉的强度足够。

2）吊环中心移至O′点时，此时按一般受力分析方法应将载荷移至螺栓组形心O，得一轴向力Q、翻倒力矩M（注意翻倒轴线的取法：按AB为轴线翻倒）。此时分析方法同上，只是工作载荷由两部分组成：轴向力Q产生的F₁及翻倒力矩产生的F₂，即

代入强度公式得

因此，吊环偏移后螺栓强度仍足够。

【实例3】 如图1-14所示，一个钢制的液压缸，缸内油压为（静载）P＝2.5MPa，内径D＝125mm，缸盖由6个M16的螺钉连接在缸体上，螺钉材料性能等级为4.6级，设螺钉的刚度c₁和缸体缸盖的刚度c₂之比为0.25。若根据连接紧密性的要求，取残余预紧力F″≥1.5F，求预紧力F′应控制在什么范围内才能满足此连接的要求。

图1-14 液压缸尺寸及受力

解：本例与前几个不同，但凡是螺栓类的设计均可归结为同样的分析方法，即螺栓组的受力分析及单个螺栓的强度计算。本题目给出压强、液压缸内径，因此可以很容易求出工作拉力。考虑螺栓属于既受预紧力，又受工作载荷作用的紧连接螺栓，该螺栓有两种失效可能性：螺钉静强度不够发生塑变或被拉断；残余预紧力不足，即连接气密性不够出现泄漏。因此预紧力既要满足强度要求，又要满足气密性要求。

（1）计算单个螺钉的工作拉力F 液压缸盖所受的总压力，此压力作用在螺栓组的几何形心，对螺栓来说是轴向拉力，每个螺钉的工作拉力为

（2）计算螺钉的总拉力F₀ 螺钉材料性能等级为4.6级，则R_eL＝240MPa，查表1-3按控制预紧力考虑，取安全系数S＝1.5，则许用应力［σ］＝R_eL/S＝240MPa/1.5＝160MPa。由强度条件可求出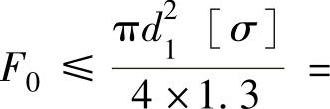

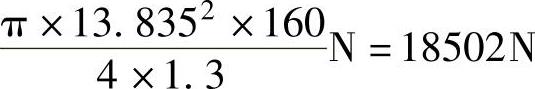
式中的13.835mm为M16螺钉的小径。

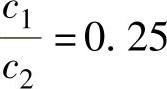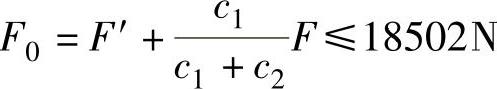（3）求预紧力F′的允许范围 按螺钉的强度条件求预紧力F′：由题目知，得，因此，可由，得到

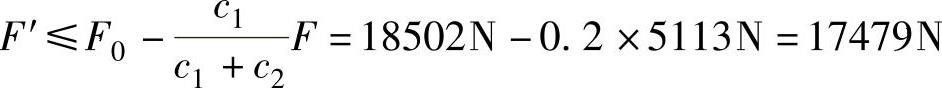
说明预紧力F′≤17479N时，根据强度条件螺钉不会被拉断。

按连接气密性条件求所需最小预紧力F′：根据题目已知条件，连接的气密性要求为F″≥1.5F，因此利用残余预紧力与预紧力的关系式，可求出预紧力：

由

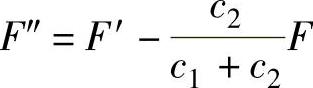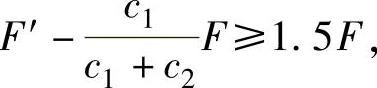
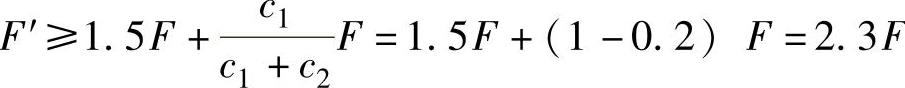得，因此有F，

即F′≥2.3×5113N＝11760N

由以上计算结果可知，既满足强度要求，又满足气密性要求的预紧力为：(www.xing528.com)

11760N≤F′≤17479N。

【实例4】 图1-15所示为一个夹紧装置，由连接螺栓夹紧，螺栓数目Z＝2，已知轴径d＝50mm，L＝400mm，W＝110N，轴与毂间的摩擦因数μ_S＝0.13，连接尺寸L_F＝28mm，可靠系数K_f＝1.3，试确定连接螺栓的直径和长度。

解法1：本例为螺栓设计，即求螺栓的直径和长度。螺栓的直径应由强度条件求得，而螺栓的长度应该参考实例中给出的结构由国家标准选择标准长度，因此，关键是由强度求螺栓的直径。与前几个实例不同的是：螺栓组的接缝面不是平面而是圆柱面，也可以近似看作平面进行计算，见本例的解法2。

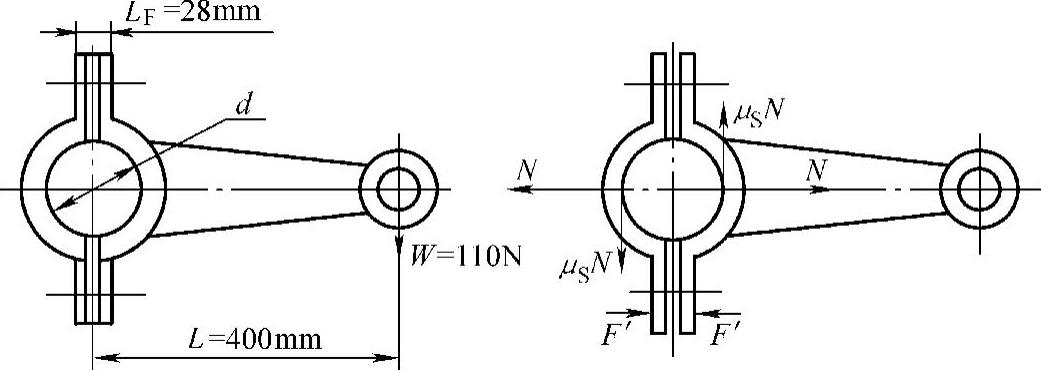
图1-15 夹紧装置结构受力图

（1）求夹紧连接螺栓的预紧力F′ 图1-15所示夹紧连接是借助于两个螺栓拧紧后，轴与毂之间产生的摩擦力来传递转矩的。假设在螺栓预紧力F′作用下，轴与毂之间的正压力为2N，且集中作用于两点，取左半毂为受力体，作用于其上的载荷如图1-15所示，显然N＝2F′。又根据连接的接合面不滑移条件，则有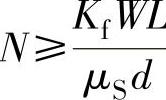，。将N＝2F′代入上式，则有

（2）确定螺栓直径 本例螺栓性能等级为4.6级，则求得R_eL＝240MPa；设螺栓为M16～M30，查表1-3按不控制预紧力考虑，取安全系数为［S_S］＝4，则螺栓的许用应力为：，代入强度公式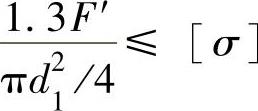，求出螺纹根径：

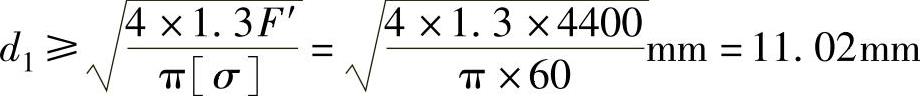
查螺纹标准，选M16的螺纹（d₁＝13.835mm），与原假设相符。

（3）确定螺纹连接尺寸 查机械设计手册选M16的螺母，高H＝14.8mm。

查机械设计手册选弹簧垫圈，厚度s＝4mm。

选螺栓：考虑到螺母H＝14.8mm，垫圈s＝4mm，已知的连接尺寸L_F＝28mm，查参考文献［2］，选粗牙六角头螺栓M16×55（GB／T 5785—2000）。

解法2：本例螺栓组连接的接合面是两个半圆柱面，因此也可以看作两个平面，即简化为三块板、两个接缝面，因此列出摩擦力矩大于外载荷的扭转力矩的平衡式，从而求出预紧力：2F′μ_S（d／2）×2≥K_fWL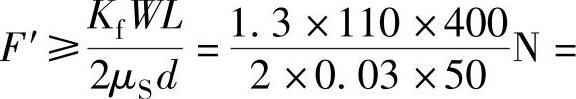，。本例螺栓组连接的接合面是两个半圆柱面，一般应当根据例中给出的条件，运用力矩的平衡关系来求解（一般夹紧装置及扳手等也多属此类）。所以，对于螺栓组连接的受力分析，不能完全靠死记硬背受力表达式，应掌握这些螺栓组连接受力分析的方法，以便灵活运用。

从本例看出：螺栓的直径由强度条件确定后，需查国家标准并标出外径M××；而螺栓的长度由连接的结构尺寸而定，在满足结构要求的情况下也需查国标，取标准长度系列值。在实际设计中还需画出结构图，此处略。

【实例5】 如图1-16a所示，托架受铅垂力P作用，托架与架体之间的摩擦因数为_μS，可靠系数K_f＝1，螺栓与被连接件的相对刚度为0.2，螺栓材料的许用应力为［σ］。列出螺栓根径d₁的表达式。

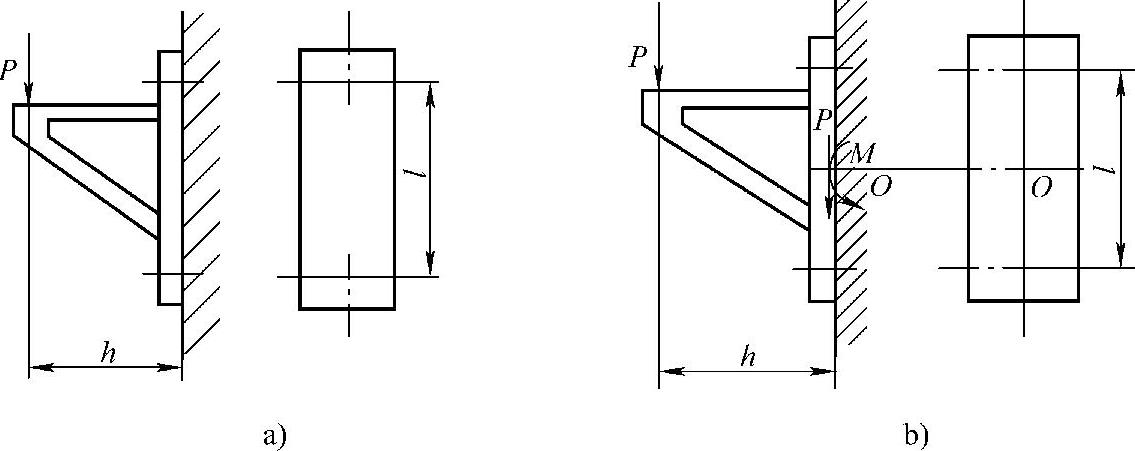
图1-16 托架尺寸及受力

解：首先将外载荷移至螺栓组的几何形心O，如图1-16b所示。对螺栓组来说外载荷是一个横向力P和一个翻倒力矩M；对单个螺栓的受力分析，应属于既受预紧力（安装前的拧紧），又受工作载荷（翻倒力矩M引起的轴向拉力）的紧连接螺栓。

（1）螺栓组的受力分析 外载荷移至螺栓组的几何形心O是：

横向力F_R＝P

翻倒力矩M＝Ph

（2）单个螺栓的受力分析 每个螺栓受到的横向力为

F_S＝F_R／2＝P／2

每个螺栓受到的由翻倒力矩引起的轴向拉力为

（3）求每个螺栓的预紧力 预紧力由底板不下滑的条件求得，即摩擦力平衡外载荷，翻倒力矩M沿底板的对称轴线翻倒，使底板上半部分的预紧力减小，但是底板下半部分的预紧力以同样的程度增大，因此翻倒力矩M对接缝面处的摩擦力没有影响。所以，底板由预紧力产生的摩擦力平衡横向外载荷，即

Zμ_SF′≥K_fF_S，得

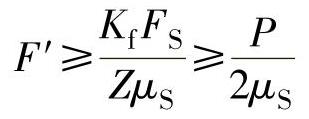
（4）计算螺栓的总拉力F₀ 假设用金属垫，设相对刚度为，则有

（5）计算螺栓的根径d₁

【实例6】 如图1-17a所示，有一个砧座用四个螺钉固定在地基上，每个螺钉的预紧力为F′，当砧上加力P后求螺钉受力大小及砧座与地基接触面压力大小，并求出螺钉的内径d₁（已知螺钉的相对刚度为K_C）。

图1-17 砧座固定在地基上的结构和受力

解：如图1-17所示，载荷已经作用在螺栓组几何形心，因此螺栓组只受轴向外载荷作用（为负值）。

（1）求每个螺钉受的工作拉力

（2）求每个螺钉的总拉力

（3）求地基的压力 如图1-17b所示，此时地基的压力应该是四个螺钉的残余预紧力之和，而不是预紧力之和。因为外力是轴向力，使预紧力发生变化，因此螺钉对地基的压力为

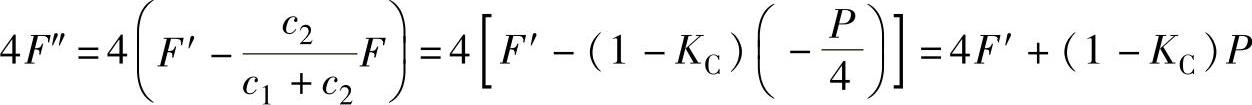
（4）计算螺钉的小径

本例螺钉小径的计算式按常规应该是用F₀代入，但是本例比较特殊，外载荷为轴向压力，因此使螺钉所受的预紧力减小，即F′＞F₀，所以应该用预紧力F′代入比较合理。当然，本例还有其他的解法，此处不列出。

【实例7】 如图1-18所示，有一个液压缸（图中未画出活塞、支座、进油接头、出油接头等零件），缸的内径D＝100mm，壁厚δ＝10mm，L＝300mm，t＝20mm，端盖、缸体、螺栓都用钢制成。缸工作压力在4MPa与0之间变化，用六个M12螺栓（小径d₁＝10.106mm）连接，螺栓性能等级为6.8级，扭紧到下屈服强度的50％。

1）假设两个端盖可作为刚体考虑，求螺栓和液压缸的刚度。

2）螺栓的平均应力和应力幅各为多少？

3）试校核螺栓的强度。

解：本例需要对螺栓的综合受力变形图、物理知识及材料力学中关于刚度等概念有较深入了解，并能灵活运用，方可求解。如图1-18所示。本例中螺栓既受预紧力，又受工作拉力，属于紧螺栓连接，因此校核螺栓的强度应根据相应的公式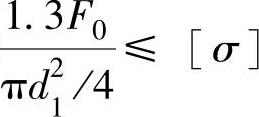进行，并且螺栓受变载荷作用，因此除了满足静力强度外，还应该验算应力幅。

图1-18 液压缸筒图

1.求螺栓及液压缸的刚度

刚度即产生单位变形量所需的力，为此，可求出预紧力F′及在该预紧力作用下螺栓及缸的伸长量，从而可求出刚度。

求预紧力F′：因例中给出螺栓性能等级为6.8级，可得R_eL＝480MPa；又由例中已知扭紧到下屈服强度的50％，由此求出预紧力F′：

求在F′作用下螺栓的变形量：

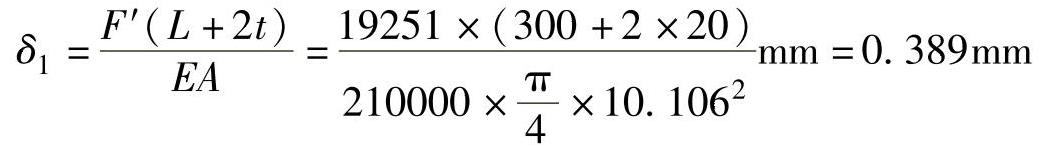
缸体在F′作用下的变形量：

因此得出螺栓的刚度c₁及缸体的刚度c₂分别为

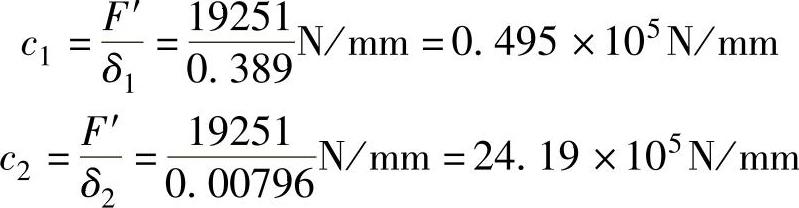
2.求螺栓的平均应力σ_m和应力幅σ_a

螺栓安装时受预紧力F′，工作时又受工作载荷F，因此螺栓工作时受的最大拉力为F₀，螺栓工作时的拉力在F′～F₀之间变化，因此可求出F₀为

螺栓在总拉力F₀及预紧力F′作用下的最大、最小应力分别为

3.校核螺栓强度

螺栓受变载作用，应分别校核静强度及疲劳强度。

螺栓的静强度校核：按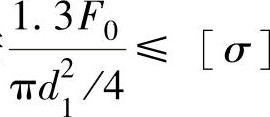计算，需先求［σ］，按控制预紧力考虑，取安全系数［S_S］＝1.5，则，因此螺栓的总应力为

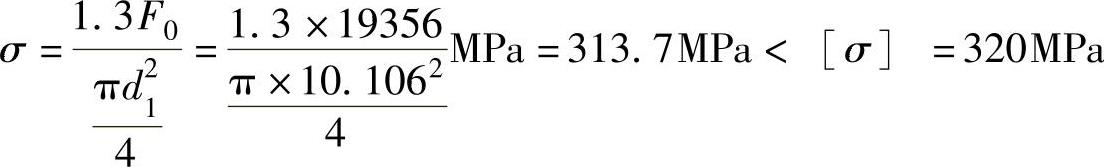
所以静力强度满足。

螺栓的疲劳强度校核：即需校核应力幅σ_a≤［σ_a］，首先必须求出许用应力幅［σ_a］：

从表1-3查得有关系数：尺寸系数ε＝1（因为螺纹为M12）；螺栓制造工艺系数K_m＝1（采用车制螺纹）；螺纹的应力集中系数Kσ＝3.9（因为已知螺栓性能等级为6.8级，可得R_m＝600MPa，查表得出）；各圈螺纹牙的受力分布不均系数K_u＝1.5（因为螺母是受拉、压）；对称循环疲劳极限为：σ_-1＝0.41R_m＝0.41×600MPa＝246MPa；取疲劳安全系数［S_a］＝3，代入上式得

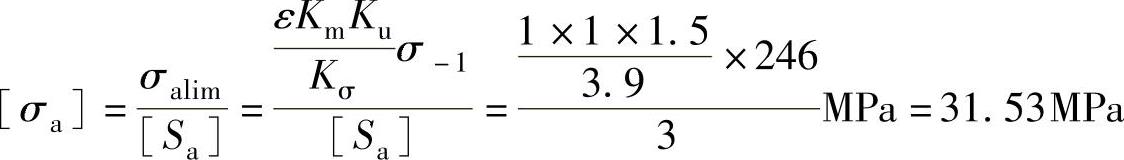
而σ_a＝0.65MPa＜＜［σ_a］＝31.53MPa，因此疲劳强度足够。