基于盘龙江严家村桥常规观测断面2014年各月监测数据，建立神经网络模型(Ⅰ)。2014年盘龙江河流严家村桥断面进行了12次数据收集，时间跨度为2014年1月～2014年12月。水文数据为观测时间的断面流量；水质数据包括水温、pH值、溶解氧(DO)、电导率、高锰酸盐指数、生化需氧量、氨氮、化学需氧量、总磷和总氮。除了化学需氧量在二月份数据未监测到，其余指标均无缺失数据。
由于输入变量包括了相应输出变量上月的数据，这样可用的样本数量为11次调查数据。对于神经网络，11组样本较少。如果样本数足够，模型对数据之间内在规律的拟合能力以及预测能力都将增加。
样本集中随机选取2个作为测试集，其余为训练集。
模型建立方法：
①输入、输出变量的预处理。处理方式为：(变量-最小值)/(最大值-最小值)。神经网络模型，无法处理有缺失的数据集，对于个别缺失数据的处理是根据最临近内插的方法将它的值计算出来。
②拓扑结构建立。
根据已有的相关资料和经验，神经网络模型(Ⅰ)含两个隐层的四层拓扑结构，即有一个输入层、两个隐含层和一个输出层。
输入层：t-1时刻严家村桥断面水温、流量、pH、电导率、溶解氧、高锰酸盐指数、生化需氧量、氨氮、化学需氧量、总磷、总氮，共有11个输入层节点。
隐层：2个隐层，第一个隐层是5个节点，第二个隐层是3个节点。(www.xing528.com)
输出层：输出层是只有一个节点，即严家村总氮浓度。
严家村桥总氮的神经网络模型结构如图4.28所示。
③模型参数设置。
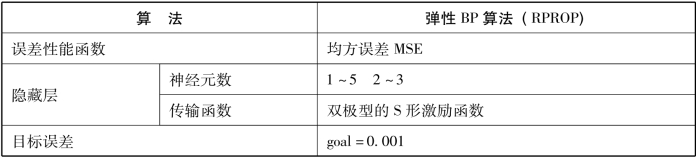
模型所使用的函数和设置的参数见表4.17。
表4.17 严家村桥总磷浓度的神经网络模型设置参数
④严家桥总氮神经网络模型。
从11个样本随机抽取9组作为模型训练集，剩余两组作为模型的测试集，构建的模型预测结果存在着高估和低估模型预测，氮两次预测的相对误差均低于20%。
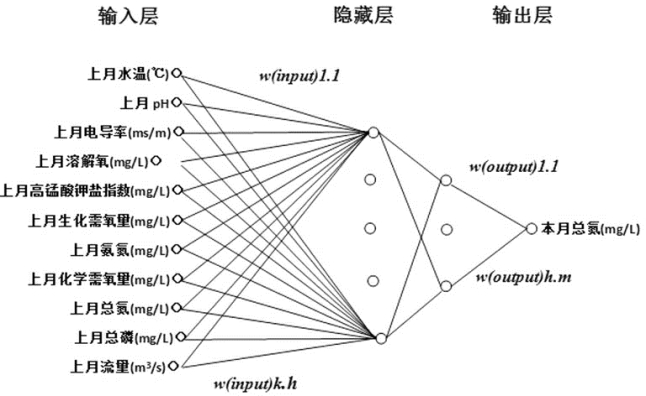
图4.28 严家桥断面总氮神经网络模型拓扑结构示意图
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
