水质模拟中污染物迁移技术原理及转换方法

3.1.2.1　水环境模拟技术原理

水环境问题是一个多维复杂过程，涉及一系列的物理、化学、生物变化。

水环境的模拟包括各种水环境指标，如悬浮物、温度、BOD、DO(溶解氧)、TP、TN、重金属以及细菌类、叶绿素a，涉及污染物在水体中的迁移和转化。针对不同水体而分为河流、湖泊、水库、海洋预测模型和水质模型。

污染物在水体中的迁移包括随流输移、分子扩散、紊动扩散和剪切离散。污染物在水体中的转化涉及有机物的衰减，水体耗氧和复氧，同一元素不同形态间的转化等。

水环境模型模拟水流状态和水质成分，包括BOD、DO、温度、藻类—叶绿素a、有机氮、氨氮、亚硝酸盐氮、硝酸盐氮、有机磷、溶解磷、大肠杆菌等。

根据项目对模型的技术要求，本次计算选用整合了水质模块、水动力模块的环境流体动力学模型(Environmental Fluid Dynamics Code，EFDC)进行模型构建，该模型具体优势如下所述：

(1)应用广泛。EFDC是由美国环保署(EPA)支持并由美国Tetra Tech公司维护开发的用于模拟湖泊、水库、海湾、湿地和河口等地表水数值模型软件，目前在河流、湖泊、河口、港湾以及湿地等水环境系统中已经有很多成功的应用实例。

(2)应用灵活并具有极强的问题适应能力。EFDC根据需要，可以用于零维、一维、二维和三维水环境模拟，EFDC是一个多任务、高集成的环境流体动力学模块式计算程序包，用于模拟水系统零维、一维、二维和三维环境的水动力—水质模型。

(3)开源性。EFDC是一个源程序公开的地表水模拟系统，它可以系统地模拟水动力、水质、富营养化和沉积物输移的动态变化及其相互影响。

(4)计算步长与输出灵活可调。EFDC的水动力计算时间步长根据计算稳定性确定，一般为秒到分钟的范围之内；输出结果的频率则可由使用者指定，一般为小时到天的范围之内。

(5)水动力与水质紧密耦合。EFDC的水动力与水质耦合在一个系统内，水动力模块经模拟计算为水质模块提供流场和温度场。水质模块利用边界条件和水动力模块提供的流场、温度场计算水体水质的时空分布。水质模块的模拟指标为多种污染物，例如TN、TP、COD和氨氮等。水质模拟计算的时间步长与水动力模型一致，形成紧密的内部耦合计算系统。

◆水动力模块

对水体水质模拟而言，由于需要了解并预测环境中流体的流动过程与流体中溶解、悬浮物质准三维空间的迁移、混合过程，就需要定量地描述研究水体的环境流体动力学特征。这些流体在垂直方向上具有本质上的流体静力学特征，同时具有边界层特征。只有对运动方程组与迁移方程组(用来描述溶解、悬浮物质的迁移、混合过程)求数值解，才能对这些流体进行实际模拟。

环境流体(具有水平尺度特征，且水平比垂直方向有更大的尺度值)控制方程组采用不可压缩、密度可变流体的湍流运动方程组这一形式，且在垂直方向具备流体静力学和边界层特征。为更加符合现实的水平边界特征，在此引入水平的曲线正交坐标系对方程组进行转换。同时，为了在垂直方向或重力矢量方向实现均匀的以水底地形和自由表面为边界的分层，需要对垂直坐标进行拉伸变换如下：

式中z*代表最初的物理纵坐标，h和ζ分别表示水底地形与自由表面在物理坐标系中的纵坐标。

对湍流运动方程组(具有垂向流体静力学的边界层)进行变换，同时对可变密度取布辛涅斯克近似(Boussinesq approximation)，可以导出动量与连续性方程组以及盐度、温度的迁移方程组。这些方程如下：

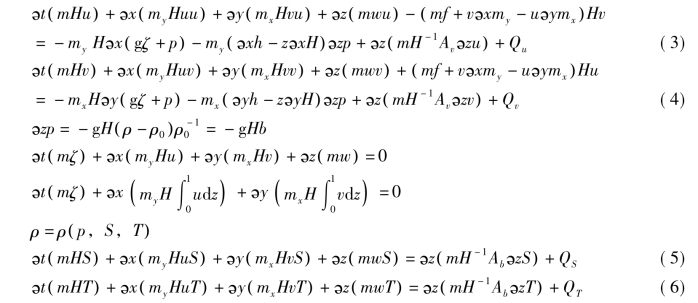
式中u、v分别表示在曲线正交坐标系中水平速度沿x、y方向的分量，mx、my分别表示度量张量沿对角线方向的分量的平方根值。m=mx·my构成了雅克比行列式或是由度量张量的平方根值所形成的行列式。在经过拉伸的、无量纲的纵轴上，用w来表示带有物理单位的垂向速度。w与物理垂向速度之间的关系表示如下：

总深度H(H=ζ+h)表示相对于物理垂向坐标原点(用z*=0来表示)水底位移与自由表面位移的总和。压强p代表实际压强减去参考密度所形成的流体静力学压强［ρ0gH(1-z)］之后，再除以参考密度(ρ0)所形成的物理量。动量方程组中，f是科氏力参数，Av指垂向湍流或称涡流黏度，Qu与Qv是动量源、汇项，将以亚网格尺度的水平扩散模型表达。对于液态流体来讲，密度ρ是温度T和盐度S的函数。浮力b是密度相对于参考值的差异进行归一化后所得到的数值。对连续性方程式在z方向上从0到1积分即可得到对深度积分的连续性方程式，此积分的垂向边界条件为w=0，z∈(0，1)。在盐度与温度迁移方程组中，源、汇项Qs与Qd包含了亚网格尺度的水平扩散过程以及热源、汇项，而Ab则代表垂向湍流扩散率。值得注意的是，如果将自由表面位置固定，则整个方程组就等价于刚性表面海洋环流的方程组，这与Clark用来模拟中尺度气态流体运动过程的地形跟踪方程组相似。

当垂向湍流黏度与扩散率以及源、汇项等已知时，构成了以u、v、w、p、ζ、ρ、S、T 8个变量为未知数的方程组。为了求解垂向湍流黏度与扩散系数，需要运用2.5阶矩湍流闭合模型，该模型由Mellor和Yamada首创，并由Galperin等人进行了改进。该模型使得垂向湍流黏度和扩散率与湍流强度(q)，湍流长度尺度l，以及理查德森数(Rq)形成如下的关系方程组：

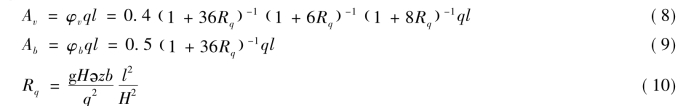
上式中的稳定函数Av与Ab分别用来描述垂直方向混合与迁移过程的弱化和强化因子(特指分别存在稳定与不稳定垂向密度分层的环境中)。通过求解如下的一对迁移方程式求解湍流强度与湍流长度尺度：

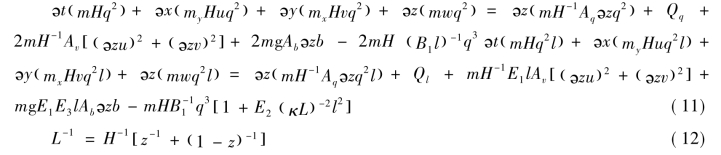
式中B1、E1、E2、E3均是经验常数，Qq与Ql是用来描述诸如亚网格尺度的水平扩散过程的附加源、汇项。垂向扩散率Aq，一般来说与垂向湍流黏度Av相等。

◆水质模块

本期水质模块采用沉降和一阶降解两个过程描述，主要用于TN、TP、COD、氨氮等污染物的模拟。

每个水质状态变量的物料守恒方程可以表示为：

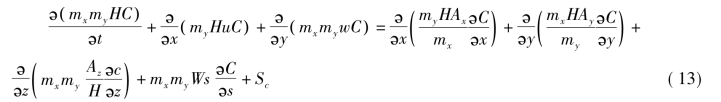
其中，C为水质状态变量浓度；u、v、w为曲线正交坐标系下X轴、Y轴和Z轴方向的速度分量；Ax、Ay、Az为湍流在相同坐标系下X轴、Y轴和Z轴方向的扩散系数；Ws为物质沉降系数(m-1)；Sc为单位体积物质一阶降解源和汇项；H为水深(m)；mx、my为平面曲线坐标标度因子。

公式(13)左边最后3项表示对流输送，右边前3项表示扩散输送；这6项物理输送与水动力模型中盐的物料平衡方程相似，因此计算方法也是相同的。公式(13)中的最后一项代表每个状态变量的降解过程及外源负荷，其公式为：

其中，K为降解系数(day-1)；Pj为第j种物质的外源负荷(kg/day)。

3.1.2.2　非永久性围隔技术原理

(1)软性围隔。围隔结构示意图见图3.1，实物照片见图3.2，围隔主体分为三部分：上部浮体(产生浮力抗拒风浪、水位变化)、中部墙体(拦截水流)以及下部石笼(固定)。

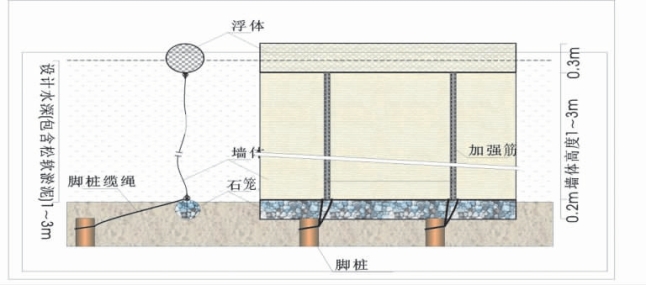
图3.1　软性围隔结构示意图

图3.2　软性围隔结构实物照片

(2)钢管土袋围堰，结构示意图见图3.3。

3.1.2.3　动态监测及调度技术原理

以在线监测技术及河口流量调度模型为手段，以目标水域的水质达到要求为目标，提出入湖河流在调度时间段内的入湖流量值(调度流量)，交由流域水资源联合调度据此实现入湖河流对目标水域的定量化补水。

(1)在线监测系统。

在线监测系统的目的在于获得补水水量水质，以及目标水域的水文水质变化情形。

在线监测系统由中心站和遥测站组成。

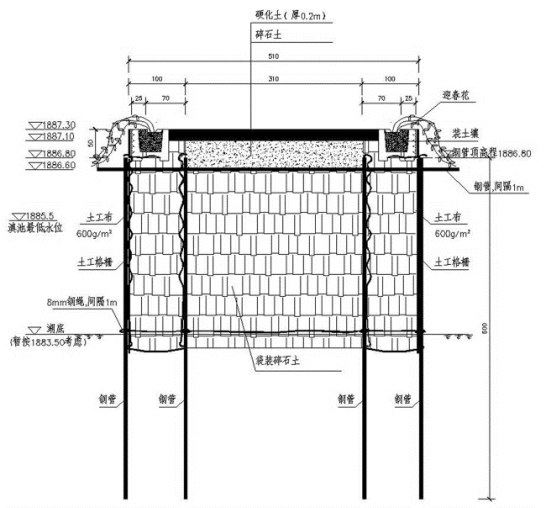
图3.3　钢管土袋围堰结构

①遥测站。

水文水质遥测站采用低功耗、高可靠性的远距离数据采集、传送装置。它能够自动实时、定时地采集水位、水质参数和终端电源电压状态，并向中心站发送数据和终端工作状态信息。

遥测终端(RTU)是遥测站的控制核心，先进的RTU具有完善的工作状态指示功能，上电自动初始化、自测试功能，以及一定范围的软、硬件故障自我保护、自检测及故障自我排除、遥测告警等智能功能。RTU能提供友好的人/机操作界面，以支持操作人员在现场完成数据检测、参数设置、附属设备(电源、传感器等)测试、RTU自诊断、人工观测数据设置、通信设备控发等工作。

②中心站。

中心站由硬件设备和系统软件组成，具有以下主要功能：

数据接收、处理：实时接收遥测站发来的数据包，自动检查数据的帧格式，并进行合理性判断，分类自动存储，立即以数的形式实时显示。判断水文水质参数、电池电压的越限状态，实时告警显示。(www.xing528.com)

通信控制：控制主机与值班机之间进行数据通信，使主机与值班机达到数据转存。当中心站联网后，通过特定的通信规约，支持网络数据共享。

文件管理：文件管理对象是原始数据文件，它主要支持文件的形成、存盘、查询、修改、转储、删除等主要功能。

显示、输出：在计算机CRT上显示单站数据、多站数据、人工输入数据、水位流量过程线、水质指标浓度过程线、测站工作状态等，可在打印机上打印。

系统管理：提供遥测站点参数设置(用于增减站点)；数据库输入、修改、插补；时钟调整；打印机、显示器参数调整；参数警戒值设置等功能。

(2)补水流量调度模型。

牛栏江—草海入湖河口水量存在丰平枯的季节性变化，同时受外流域水资源调配的影响，来水量变幅较大。为确保承接入流的湖泊局部水域的水质改善达到预期目标，本书将建立基于河道水质浓度识别的河口水量调控技术，以草海水质改善为目标，优化草海补水的年补水量与补水运行方式。

从技术来说，水资源调度需要综合考虑多方面的因素，给出不同时段、不同条件下的最优调水策略，而任意一时刻的水质是之前调水影响的总和，所以该问题是一个动态优化问题。与单纯的水量调度不同，调水策略的实施与水质的充分响应存在时间滞后，这关系到如何评价某个策略的效果，也就是在动态优化问题中的回报函数以及状态变量。所以这要求分析任意一时刻水质受到前述所有决策的影响大小，并据此判断回报函数的形式。同时，水资源调度问题也是一个多目标优化问题。调度以水质改善为主要目标，同时兼顾调水水量、水位以及工程能力等多种因素，所以调度问题还可以扩展为一个多目标动态优化问题。

目标水域建立高精度模型可以得到调水水质(TN、TP)、水量与目标水域内水质(TN、TP、Chl.a)的响应关系，即通过模型模拟可以得到数据集：

其中t表示模拟时间，lakestate=(laketn，laketp，lakechla)表示目标水域在t时刻的TN、TP以及叶绿素a的浓度，riverstate=(rivertn，rivertp)表示t时刻的调水水质即TN、TP的浓度，diversion表示在t时刻所采取的措施，即调入的水量，#F表示所含数据对的个数。数据集是在模拟时间下湖泊和调水的水质状态、决定调入的水量以及湖泊的响应和未来水质变化情况所组成的观测数据对，可以通过一次模拟或多次模拟产生。

基于此数据集，希望得到一组控制策略，使得在保证水质达标的情况下，将调水水量控制到最小，以更有效地在流域内分配利用调水水量。由于有最小水量的要求，调水水质也有可能劣于湖体水质，但由于调水的水质与水量与示范区内的水质并不是严格的一一对应的关系，存在非线性、时滞性以及随机性，一个时刻的决策会对下一时刻的决策产生影响，故应考虑使得累计调水量最小(t时刻的调水量加上t+1时刻调水量的期望以及后续调水量的期望)，同时将调水水量与示范区水质响应的期望作为效益或系统的回报，即：

其中回报函数可以是一个带有随机项的函数，并且受到决策时间例如季节因素的影响，在本问题中具体的形式为：

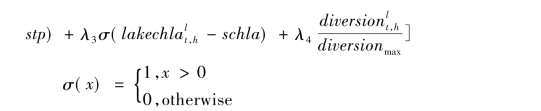
负号是为了使得目标函数最大化，前三项分别表示水质指标达标情况，对回报函数惩罚以达到满足约束的目的，第四项表示相对调水量的大小，为调水量的大小与最大允许调水量的比值，λ表示各项之间的权衡，并且要求。由于模型模拟可以给出比调水更小尺度的数据，为了精确合理评估随机性，对t到t+1之间模型所有H个输出结果都进行评价，相当于得到时间尺度上的达标率(意味着可以用模拟模型更好地估计调水的效果，这也是实地实验观测所做不到的，就是利用更小尺度的数据来评价达标的效果)。

这样设置回报函数也是为了方便对最优决策中调水量的分析，以及增加模型的多目标的可扩展性。那么最优的调水策略就是使得累计回报最大。

为了使得问题可以更好地利用现有方法进行处理，需要作以下假设：

①t时刻的调水水量即本问题所需要寻找的决策，只依赖于t时刻的来水水质、湖泊水质以及所做出的时间t，即diversiont=π(lakestatet，riverstatet，t)，π表示从状态到决策的一种映射关系，也就是在任意状态下的策略函数。

②假设调水策略只根据当日的水质状况做出，但同时会考虑未来的随机性变动。

③考虑到季节等因素，本方案假设存在一个周期性的最优控制策略，结合示范区的换水周期，且这个周期不超过12个月。

④t时刻的来水水质与t+1时刻的来水水质存在一定的关系，t+1时刻的来水水质可以是t时刻来水水质以及时刻t的任意未知的概率分布，但是这个分布是存在的。当调水调度水量变化的频率比较高的时候，这个假设显然可以接受。而当频率较低，也就是两次更换调水水量的时间间隔较长的时候，可以认为t+1时刻与t时刻水质毫无关系，那么t+1时刻就服从于一个只依赖于时间t+1(也就是时间t)的概率分布(例如来水水质的随机性只受到季节的影响)，这个假设依然可以接受。

由于

第二项随着T取值的增加衰减速度较快，相比较第一项而言可以忽略，所以累计回报可以近似为有限时间内的累积回报。注意到diversiont=π(lakestatet，riverstatet，t)，那么所要寻找的最优化策略就是：

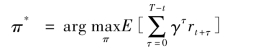
根据随机动态规划理论(Stochastic Dynamic Programming)中的随机逼近法(Stochastic Approximation)，上式中的最优解π*为方程的一个不动点，引入Q函数：

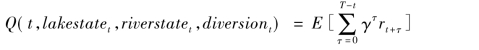
则最优解可以通过下式的贝尔曼方程(Bellman Equation)迭代计算获得：

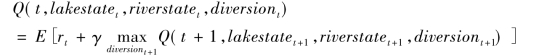
Q函数的引入避免了从t到t+1时刻的状态转移的估计，而最优策略是从下式获得：

模型求解算法：

机器学习中的增强学习(Reinforcement Learning，RL)算法经常被用来对模型求解。RL与监督学习、无监督学习类似，是指一种特殊的学习环境，也就是在观测值有限或观测代价比较高的情况下开发出的一种寻优算法。观测的代价来源于两个方面，一方面是模型结构，对于马尔可夫过程而言是状态转移函数与回报函数的估计代价；另一方面是观测的数量，观测的数量随着变量的增加会急剧增加。RL算法又分为规划算法(Planning Algorithm)和学习算法(Learning Algorithm)。规划算法是指在状态转移函数和回报函数已知的情况下的算法，学习算法是在模型未知的情况下的算法，而学习算法又分为基于模型(Model Based)和不依赖于模型(Model Free)的算法，基于模型是指算法先学习模型的结构再基于模型的结构寻找最优策略，而不依赖于模型的算法是直接通过观测数据学习最优策略，在RL中应用最为广泛的Q学习算法就是一种不依赖于模型的学习算法。

但是Q算法是一种在线学习算法，要求算法与模型之间有交互作用，并且Q学习算法虽然避免了对模型结构的估计但是没有避免采样维数的问题。针对此问题，(Ernst，Geurts，& Wehenkel，2005)开发出一种基于回归树的批量增强学习算法(Tree Based Batch Mode Reinforcement Learning)称为FQI(Fitted Q-Iteration)。同样采用了Q学习中的Q函数进行迭代回归，所不同的是这是一种离线学习(Offline Learning)方法，观测数据一次性获得，Batch Mode体现在每次算法迭代的过程中会用到所有的观测数据，而不是像其他RL算法一样每次迭代只用一个观测数据，另外FQI算法用回归树(Tree Based)的方法对Q函数进行拟合(Fitted)，这样就可以对本来被离散化的决策空间连续化，从而对所有可能的决策进行估计和迭代。FQI算法要求回归模型在概率上是基于最小平方误差(Least Squares Regression)的，这样回归模型才能估计观测数据下的回报函数以及Q函数的条件期望。除此之外，要求回归模型最好是非参数模型，因为输入输出的响应关系一般难以实现确定形式，而用得最多的神经网络方法虽然可行，但是算法参数过多，以及在过拟合和训练时间上和在FQI框架上都不是特别适用，所以回归树的方法有了天然的优势。

具体在回归模型的选择上，(Ernst et al.，2005)建议采用Extra Tree的方法，这一种基于Boosting原理开发的随机回归树模型，随机创建多个回归树，并对所有回归树进行模型平均后输出结果，可以有效降低回归的偏差以及方差(Geurts，Ernst，& Wehenkel，2006)，虽然Extra Tree的方法不能保证FQI算法的收敛，但总是能取得较好的精度(Ernst et al.，2005)。Castelletti，Galelli，Restelli，& Soncini-Sessa(2010)，Ernst et al.(2005)讨论了Extra Tree算法参数设计的问题，并结合FQI算法给出了参考的设计值。本次所采用的Extra Tree算法代码来源于(Taormina，2014)。

对于调水问题而言，湖泊水质的响应受季节性因素等影响较大，所以不同季节或月份采取的策略也不尽相同，针对此问题，Castelletti et al.(2010)对FQI算法在数据处理上做了改进，将时间作为一个状态变量，由此产生的最优策略蕴含周期性。另外，本问题的回报函数采用了罚函数的方法，并加入了权衡系数，所以采用多目标的分析方法会有利于最优决策的选择，Pianosi，Castelletti，& Restelli(2013)讨论了在此情况下的处理方法。但是本问题只关心权重的设置是否会产生较大的影响，暂不作为多目标问题。总体来说，此时回归算法Extra Tree的输入和输出分别为：

其中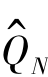表示回归算法在第N次迭代中对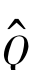函数的拟合估计，在求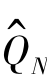关于调水量的最优值的时候，由于本问题的决策变量只有一个，故采用离散化区间的方法进行遍历搜索，当维数较高的时候可以考虑其余智能寻优算法。

所以求解算法流程如图3.4所示。

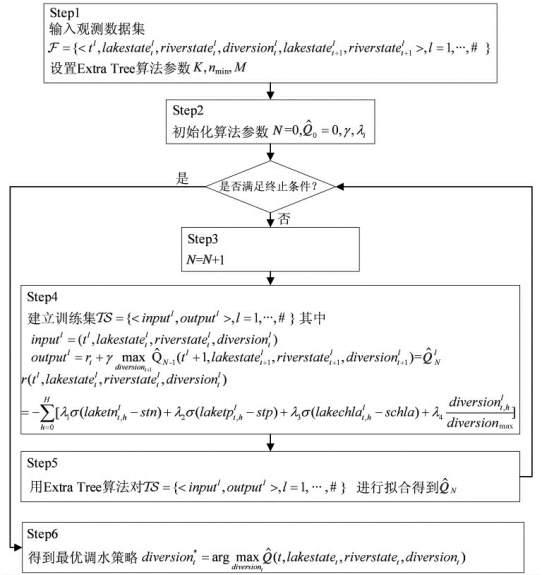
图3.4　示范区调水量的FQI算法求解流程图

当N=1时建立的训练集实际上是在输入与瞬时回报时间上建立拟合关系，也就是说有：

算法参数校正：

算法参数主要确定Extra Tree中的M以及nmin，探讨其对FQI算法的影响。M主要决定了Extra Tree在拟合过程中每次拟合的差异性，取值越大所需要的计算时间越长。在nmin取值15、M取值从1到70的情况下，拟合值与真实值的方差如图3.5，其中方差是通过10次重复模拟得到的上下界。

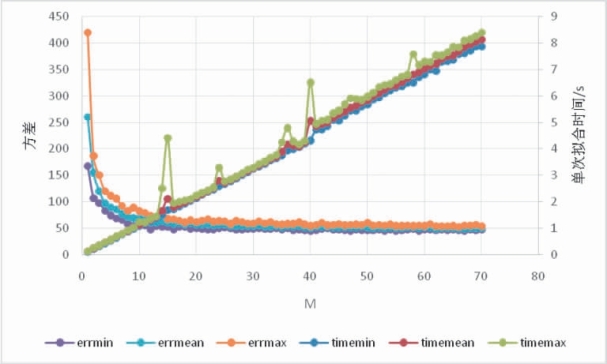
图3.5　M取值的算法性能变化

训练时间随着M的增加而线性增加，每次训练的差异性即方差的变动随着M的增加而减少。最终方差收敛到的极限是由nmin所决定的。在M取值15的情况下，nmin从1到500取值，拟合值与真实值的R2变化如图3.6，其中R2的变动是在相同的参数下重复运行10次算法得到的上下界以及均值。

值得注意的是，nmin的取值也会影响计算时间，nmin取值越大，计算时间越短。图3.6表明，nmin取值400的时候，R2仍旧是可以接受的，nmin取值过小则有过拟合的危险。这取决于数据的随机程度，如果随机程度比较大，那么要求nmin的取值较大，提高模型的泛化能力。

最终确定M以及nmin大小还有一个比较重要的方面是gamma为0的时候最优决策的变动。按照Q学习的机理，gamma为0的时候算法应该第一次就能收敛到一个不动点。但是考虑到在拟合过程中Extra Tree结构的变动，可能并不能完全收敛，但是差异性不大。在这个时候，nmin以及M的取值就决定了这个拟合算法的泛化能力以及训练不确定性的大小是否合适，经过试验，结合上面结果，M取值为200，nmin取值为200，另gamma取值0.5。在迭代次数上，由于gamma取值不大，算法在第10次即可收敛，在运算时最大迭代次数取50。

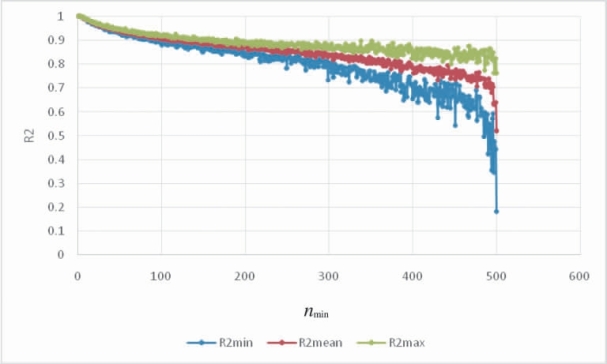
图3.6　nmin取值的算法性能变化

根据FQI算法的意义，当训练集足够大的时候，所拟合的Q函数接近于真实Q函数。数值实验分析发现，当训练集合的调水情景达到40个的时候，收益函数的均值几乎没有发生改变，部分情况下的方差比较大。鉴于模拟模型的时间成本很高，所以推荐的训练数据情景个数最低为40。即需要40次情景试验，每次情景试验包含了一年的调度以及水质响应情况，加上一年前后各一次调度，实际上一年包含24+2个周期，即总的调水周期是26×40=1040个。