【摘要】：图6-24自回归模型功率预测误差校正实现流程示意图误差校正方法的关键是对误差进行分析和建模，常用的误差校正方法有自回归模型、卡尔曼滤波法、偏最小二乘法等，其中自回归模型在误差趋势预测中有较好的应用，其实现流程如图6-24所示。
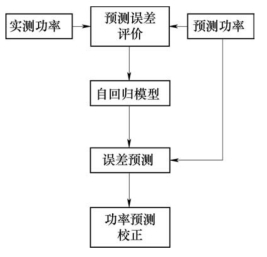
图6-24 自回归模型功率预测误差校正实现流程示意图
误差校正方法的关键是对误差进行分析和建模，常用的误差校正方法有自回归模型、卡尔曼滤波法、偏最小二乘法等，其中自回归模型在误差趋势预测中有较好的应用，其实现流程如图6-24所示。在实践中，一般通过对实测功率与预测功率的误差进行自回归建模预测，实现对未来预测误差的估计，以此校对预测值来提高超短期预测精度。
若历史预测误差值为｛xt｝，白噪声序列表示为｛at｝，回归系数用φj（j=1，2，…，p）表示，可得到的自回归模型为：
若样本观测数为N，记
则自回归模型可以表示为：
(https://www.xing528.com)
由最小二乘原理可得到模型参数的估计为：
那么根据最小二乘估计值可以得到噪声的估计值为：
噪声方差
的最小二乘估计值为
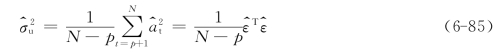
误差校正属于提高预测精度的辅助手段，当误差呈现出一定规律性时，误差校正效果明显；当误差随机性较强时，误差校正效果不明显，甚至有校正失误的风险。总体上说，在预测模型确定且长期较稳定运行的前提下，预测误差校正对预测精度的提高起到重要作用。图6-25展示了西北某光伏电站进行功率预测误差校正的效果，从功率误差序列可以看出校正效果较为明显。
图6-25 功率预测误差校正效果图
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
