SVM预测模型优化

6.5.2.1　SVM基本原理

1.VC维与风险结构最小化

传统的智能预测模型的样本学习过程都在执行非线性逼近和拟合的任务，其预测性能的主要表征即是它的泛化能力。传统的各种学习方法中普遍采用经验风险最小化原则，在样本数量有限的情况下是不合理的。从统计学习理论出发，应该同时最小化经验风险和置信范围，针对这一需求，提出统计学习理论中的一个新策略，即把函数集构造成函数子集的序列，使各子集按VC维大小排列，然后从每个子集中，寻找最小的经验风险，在子集之间折衷考虑置信范围和经验风险，以取得实际的最小风险，这种思想就是结构风险最小化（Structural Risk Minimization，SRM），结构风险最小化原理如图6-13所示。

图6-13　结构风险最小化原理

人工神经网络是基于经验风险最小化原理来对目标进行优化，易陷入局部最优，训练结果不够稳定，通常需要大量的训练样本；而支持向量机有严格的理论和数学基础，基于结构风险最小化原则，泛化能力优于前者，能够确保全局最优性。

2.SVM基本原理与核函数

SVM算法是从线性可分情况下的最优分类面（Optimal Hyperplane）提出的。所谓最优分类面就是要求分类面不但能将两类样本点无错误地分开，而且要使两类的分类间隔最大，最优超平面如图6-14所示。

图6-14　最优超平面示意图

d维空间中线性判别函数的一般形式为g（x）=wTx+b，分类面方程是wTx+b=0，我们将判别函数进行归一化，使两类所有样本都满足｜g（x）｜≥1，此时离分类面最近的样本满足｜g（x）｜=1，而要求分类面对所有样本都能正确分类，即满足：

式（6-43）中使等号成立的那些样本叫做支持向量（Support Vectors）。

两类样本的分类间隔（Margin）如图6-14所示，其大小为：

因此，最优分类面问题可以表示成如下的约束优化问题，即在式（6-43）的约束下，最小化函数：

若在原始空间中的简单超平面不能得到满意的分类效果，则必须以复杂的超曲面作为分界面，于是引入核函数的概念。首先通过非线性变换φ将输入空间变换到一个高维空间，然后在这个新空间中求取最优线性分类面，而这种非线性变换是通过定义适当的核函数（内积函数）实现的，令：

用核函数K（xi，xj）代替最优分类平面中的点积xTixj，就相当于把原特征空间变换到了某一新的特征空间，此时优化函数变为：

而相应的判别函数式则为：

式中　xi——支持向量；

x——未知向量。

式（6-48）就是SVM，在分类函数形式上类似于一个神经网络，其输出是若干中间层节点的线性组合，而每一个中间层节点对应于输入样本与一个支持向量的内积，因此也被叫做支持向量网络，如图6-15所示。

图6-15　支持向量网络(www.xing528.com)

由于最终的判别函数中只包含未知向量与支持向量内积的线性组合，因此计算复杂度取决于支持向量的个数。

目前常用的核函数形式主要有以下三类，它们都与已有的算法有对应关系。

（1）多项式形式的核函数，即K（x，xi）=［（x·xi）+1］q，对应SVM是一个q阶多项式分类器。

（2）径向基形式的核函数，即K（x，xi）=exp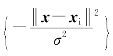，对应SVM是一种径向基函数分类器。

（3）Sigmoid核函数，如K（x，xi）=tanh［v（x·xi）+c］（tanh表示双曲正切函数），则SVM实现的就是一个两层的感知器神经网络，只是在这里不但网络的权值、而且网络的隐层节点数目也是由算法自动确定的。

3.支持向量回归机（SVR）

SVR算法的基础主要是ε不敏感函数（ε-insensitive function）和核函数算法。目的是寻找和优化回归泛化边界，依赖用于忽略错误的损失函数的定义，这些错误数据落在距真值某一范围之内。这类函数通常被称为显示密集损失函数。图6-16展示了一个带有显示密集带的SVM非线性回归的实例。其中，变量确定错误训练样本点的代价，在显示密集带内所有点都为0。

图6-16　SVM非线性回归

支持向量分类和回归问题中一个重要的观点：使用训练点的较小子集来解决问题可产生极大的计算量优势。使用显示密集损失函数，保证了全局最小值的存在，同时也确保了可靠的泛化边界。

设训练样本集为：（y1，x1），（y2，x2），…，（yn，xn），x∈Rn，y∈R，回归函数用下列线性方程表示：

回归的精确性由损失函数确定，支持向量回归采用了一种由Vapnik提出的新型损失函数（ε-insensitive损失函数），即不敏感损耗函数Le（y）：

支持向量回归通过ε在高维特征空间中进行线性回归分析，同时通过最小化‖w‖降低模型复杂度，可以通过引入松弛变量确定ε-insensitive区域之外的训练样本集的误差。根据最优化原理，最终求解得逼近方程为：

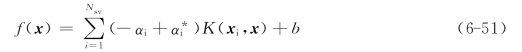
式中　Nsv——支持向量数；

K（xi，x）——核函数。

支持向量回归机的推广性能（估计精度）决定于变换参数C，ε和核函数参数的设置。

参数C决定模型复杂度和误差容忍度之间的平衡。参数ε控制ε延迟区域的宽度，用于适应训练数据。ε的值能够影响支持向量的个数，一方面，ε值越大，选择的支持向量越少。另一方面，ε值越大，得到的估计结果越平滑。因此，C和ε的取值在不同的方面影响着模型的复杂度。

事实上，支持向量机模型的泛化能力依赖于三个参数的共同作用，这增加了选择最佳参数的复杂性。选择特定的核函数类型和核函数参数通常要基于应用领域的知识，并且要反映训练数据输入值的分布情况。

6.5.2.2　风速预测建模

基于SVR的风速超短期预测建模，目的是为了建立一个风速与输入因子之间的逼近方程，这种关系显然是非线性的，势必就要选择合适的核函数实现非线性映射。

根据6.5.1.2节中风速预测因子的选取，将风速、气温、气压、湿度、风向分别表示为xi（i=1，2，…，5），组成的输入因子向量为x=（x1，x2，x3，x4，x5）T，输出因子为风速值W。基于式（6-51）可建立逼近方程（6-52）用于风速超短期预测，其中W（t）表示预测时刻的风速值，x（t）表示预测时刻的输入因子值，预测时刻输入因子值可通过数值天气预报获得，也可以分别预测。

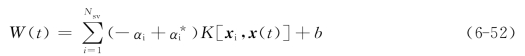
6.5.2.3　太阳辐射预测建模

根据6.5.1.3节中太阳辐射预测因子的选取，将大气层外辐射、气压、湿度、压强、大气质量和清晰度指数分别表示为xi（i=1，2，…，6），组成的输入因子向量为x=（x1，x2，x3，x4，x5，x6）T。输出因子为预测时刻的太阳辐射值I。基于式（6-51），可建立逼近方程式（6-53）用于太阳辐射超短期预测，其中I（t）表示预测时刻的太阳辐射值，x（t）表示预测时刻的输入因子值，预测时刻输入因子值可以通过数值天气预报获得，也可以分别预测。