使用ANN预测模型进行预测

人工神经网络模型有很多种，常用的回归逼近器是BP-ANN和RBF径向基函数（Radical Basis Function，RBF）网络。在上一节中BP-ANN模型被设计为时间序列预测模型，输入、输出层均为时间序列值。事实上，BP-ANN也可以用于多因子预测模型，只是建模思路和模型结构有所差异。BP-ANN的相关理论已在6.4.3中介绍。本节将主要介绍RBF神经网络相关内容。

6.5.1.1　RBF神经网络基本原理

RBF神经网络模型起源于多变量插值的径向基函数方法，不同于BP-ANN对映射的全局逼近，RBF使用局部指数衰减的非线性函数对输入输出进行局部逼近。这意味着达到与BP-ANN相近的精度，RBF神经网络所需要的参数要相对少。在任意非线性函数逼近和系统内在复杂规律性的描述方面，RBF神经网络的适用性较强，并且具有极快的学习收敛速度。鉴于上述优点，RBF神经网络较为适用于非线性函数的模拟学习，在多因子超短期预测中可以取得较为理想的应用效果。

1.网络结构

从结构上看，RBF神经网络属于多层前向神经网络。RBF神经网络结构如图6-10所示，输入层含有多个神经元，输出层是对输入模式的映射。隐含层有N个神经元，第j个隐单元的激励函数选取高斯函数，高斯函数是对中心点径向对称且衰减的非负非线性函数，输出为：

式中　X（t）——t时刻一组输入训练样本；

C（t）——t时刻高斯函数的中心；

σ——高斯函数方差。

图中wi（t）（i=0，1，…，N）表示t时刻隐含层与输出层的权值。

在图6-10中还设置了阈值φ0=1，相当于一个隐含层的输出恒为1，表示存在一个输出恒为1的隐含层神经元，从而建立了一个广义RBF神经网络。

图6-10　RBF神经网络结构示意图

2.参数训练

RBF神经网络需要学习的三个参数为基函数的中心、方差以及隐含层与输出层间的权重。根据径向基函数中心选取方法的不同，RBF神经网络有多重学习方法。其中，最常用的四种学习方法是随机选取中心法、自组织选取中心法、有监督选取中心法和正交最小二乘法。

在实际应用中，一般选择基于K均值聚类算法的自组织选取中心法；基函数方差用σ=dmax确定，其中dmax为选取基函数中心之间的最大距离；隐含层与输出层间的权重用最小二乘法确定。

下面给出隐含层至输出层神经元之间权系数的具体学习算法。设隐含层共有N个RBF神经元，当隐含层神经元的权值wi确定后，由图6-10可知，神经网络的输出为：

RBF神经网络的学习属于有监督学习，神经网络权系数的学习可以视为多元线性函数的极值求解问题。因此，可利用各种线性优化算法求得各神经元的连接权系数，如梯度下降法、递推最小二乘法等。若第k次迭代网络输出值是Out（k），目标值为tp（k），定义目标函数如下：

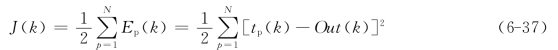
按照负梯度方向调整网络权系数，即

(www.xing528.com)

若按照递推最小二乘法调整网络隐含层到输出层的连接权系数，即通过调整wj（其中j=1，2，…，M，M是隐含层节点数），使得

其中w（k）=［w1　w2　…　wN］。

于是可以得到最小二乘递推算法如下：

经多次迭代，当目标函数J（k）小于某一设定值时被认为迭代收敛，停止迭代并确定了网络的权系数，从而完成预测模型的训练。

3.网络特性

普通RBF神经网络采用的是高斯函数。采用高斯函数作为基函数的优点是表示形式简单、径向对称、光滑性好。由于该基函数表示简单且解析性好，任意阶导数均存在，能够有效克服多变量输入下的复杂性问题，便于进行理论分析。

对于RBF神经网络而言，其输出节点计算是隐层节点给出的基函数的线性组合，其隐层中的基函数对输入激励产生一个局部化的响应，即每一个隐节点有一个参数向量c，称之为中心，该中心用来与网络输入样本向量相比较，以产生径向对称响应，仅当输入样本落在输入空间的某个局部区域时，隐节点才做出有意义的非零响应值，响应值在0～1之间，输入与基函数中心的距离越近，隐节点响应越大，而输出单元一般是线性的，即输出单元是对隐节点输出进行线性加权的组合。

RBF神经网络只有少数几个权值影响网络的输出，在训练时也只有少数权值需要进行调整，而且训练速度明显提高，训练步数的显著减少使得RBF神经网络的学习速度大大提高。与BP神经网络以及采用改进BP神经算法的前向网络训练结果作比较，RBF神经网络所用时间较短，且在多数情况下表现出更优的函数逼近能力。有理论证明，在前向网络中，RBF神经网络是完成映射功能的最优网络。

6.5.1.2　风速预测建模

人工神经网络模型建模的关键是对模型的输入、输出变量的确定以及模型结构和参数的优化。后者在机器学习领域已经有很多成熟的研究，已有很多值得借鉴的理论依据，这里就风速超短期预测重点讨论模型的输入、输出变量的确定。

一般情况下，输入因子的选取原则是对风速影响显著、易量化，可常规监测和采集。根据本书第2章、第3章和本章6.2节风的超短期变化影响因素相关内容，选择历史风速、气温、气压、湿度、风向为神经网络模型的输入因子。当然，因子的选取并不局限于此，其他量化的输入因子也可经因子筛选、检验，逐步加入或者对已选因子进行删减。这要根据研究地点具体的环境气象条件决定，从模型的角度可以通过预测效果来进行因子筛选，也可以通过神经网络训练过程中因子的权重大小来取舍。总之，考虑的因子不宜过多，否则会增加模型的复杂度，因子过少，又会降低预测的准确性。

图6-11是基于ANN的风速超短期预测模型示意图，可以是BP-ANN也可以是RBF-ANN，都选择三层网络结构。其中，输出因子为风速预测值，输入因子为风速、气温、气压、湿度、风向等气象要素值。

图6-11　基于ANN的风速超短期预测模型示意图

6.5.1.3　太阳辐射预测建模

在太阳辐射超短期预测建模中，建模思想和风速超短期预测类似，首先需要进行输入因子的选择。根据本书第2章、第3章和6.3节太阳辐射的超短期变化影响因素相关内容可知大气层外的太阳辐射是地表辐射的直接来源，可以通过理论公式计算得到；大气质量对地表辐射也有影响且可理论计算；气温、湿度、压强这几个基本的气象因子间接反映了天气状况，它们与辐射衰减有关；云、气溶胶、空气分子的影响可统一用清晰度指数来表示。

基于人工神经网络建立预测模型，模型输入输出因子的选择至关重要，直接关系到模型的性能与精度。目前，预测方法研究大多集中在对模型结构和算法的优化上，而对模型输入输出因子的分析和筛选缺乏足够重视。

图6-12是基于ANN的太阳辐射超短期预测模型结构示意图，采用三层网络结构。其中输出因子为预测时刻的太阳辐射，输入因子为预测时刻的大气层外辐射、气压、湿度、压强、大气质量和清晰度指数。在实际应用中，输入因子的预测值一般通过数值天气预报或者统计方法获得，然后结合本节模型最终实现太阳辐射预测。

图6-12　基于ANN的太阳辐射超短期预测模型结构示意图