使用BP-ANN模型进行预测优化

BP-ANN，即BP神经网络（Back Propagation Artificial Neural Network），是一种按误差逆传播算法训练的多层前馈网络，是目前应用最广泛，也是最基本的神经网络模型之一。

BP神经网络能够学习和存贮大量的输入—输出模式映射关系，这种关系可以是线性关系也可以是非线性关系。其学习规则采用梯度下降法，通过反向传播来不断调整网络的权值和阈值，使网络的误差平方和最小。该网络具有很强的鲁棒性和容错性，能实现自学习、自组织和自适应，可以充分逼近任意复杂的非线性系统。

鉴于风速、太阳辐射时间序列体现出的复杂非线性时序特征，本节讨论如何利用BP神经网络实现风速和太阳辐射的超短期预测。

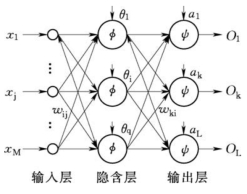
图6-4　BP神经网络结构示意图

6.4.3.1　基本原理

基本BP神经网络算法包括两个方面：信号的前向传播和误差的反向传播。即计算实际输出时按从输入到输出的方向进行，而权值和阈值的修正从输出到输入的方向进行。

如图6-4所示为BP神经网络的结构。

其中：

xj表示输入层第j个节点的输入，j=1，…，M；

wij表示隐含层第i个节点到输入层第j个节点之间的权值；

θi表示隐含层第i个节点的阈值；

φ（x）表示隐含层的激励函数；

wki表示输出层第k个节点到隐含层第i个节点之间的权值，i=1，…，q；

ak表示输出层第k个节点的阈值，k=1，…，L；

ψ（x）表示输出层的激励函数；

Ok表示输出层第k个节点的输出。

1.信号的前向传播过程。

隐含层第i个节点的输入量neti为

隐含层第i个节点的输出量yi为

输出层第k个节点的输入量netk为

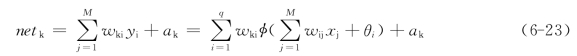
输出层第k个节点的输出量Ok：

2.误差的反向传播过程

误差的反向传播，即首先由输出层开始逐层计算各层神经元的输出误差，然后根据误差梯度下降法来调节各层的权值和阈值，使修改后的网络最终输出能接近期望值。对于每一个样本p的二次型误差准则函数Ep为

系统对P个训练样本的总误差准则函数为：

在BP-ANN进行模型训练的过程中，不断进行误差的反向传播，并调整权重和阈值，直至输出层误差小于某一阈值表示模型学习完成，然后就可以将学习好的模型用于预测，如图6-5所示为BP-ANN算法流程图。

6.4.3.2　时序预测建模(www.xing528.com)

神经网络模型建模的基本准则是输入层输入因子与输出层输出因子之间有较强的相关性。对于时间序列预测问题，根据上节ARMA模型的介绍中提到过的自相关函数与偏相关函数以及模型定阶的相关分析来确定输入输出因子。自相关函数刻画了时间序列相邻变量之间的相关性，偏相关函数则是排除了其他中间变量的影响，真实地反映两个变量之间的相关性。

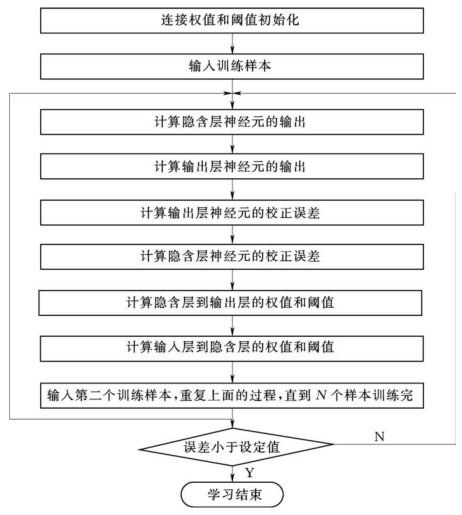
图6-5　BP-ANN算法程序流程图

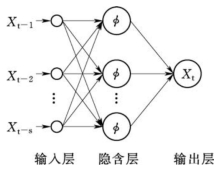
图6-6　基于BP-ANN的时间序列预测模型

基于BP-ANN的时间序列预测模型中，输出层节点一般选t时刻的预测值，输入层节点选择Xt-1，Xt-2，…，Xt-s，其中s是根据时间序列分析确定的阶数，基于BP-ANN的时间序列预测模型如图6-6所示。

对于基于BP-ANN的风速、太阳辐射超短期预测模型，需要重点关注的是其泛化能力，这将直接关系到预测的性能和精度。从人工神经网络理论的角度，目前已发现许多影响模型泛化能力的因素，包括网络结构复杂性、训练样本数量和质量、网络的初始权值、学习时间、目标函数的复杂性，以及对目标函数的先验知识等。但是在这些因素中，除了网络结构和训练样本数对泛化能力的影响具有一些定量结果外，其余因素对泛化能力的影响还只有定性解释。结合目前的工程经验和理论基础，对神经网络预测性能的提升主要依靠算法优化和结构设计。

6.4.3.3　算法优化

BP-ANN算法因其简单、易行、计算量小、并行性强等优点，目前是神经网络训练采用最多也是最成熟的训练算法之一。针对此方案通常存在的学习效率低、收敛速度慢以及易陷入局部极小值等问题，在网络结构和学习原理方面可以采用以下几种改进措施。

1.附加动量法

附加动量法使网络在修正其权值时，不仅考虑误差在梯度上的作用，而且考虑在误差曲面上变化趋势的影响。在没有附加动量的作用下，网络可能陷入浅的局部极小值，利用附加动量的作用有可能滑过这些极小值。

带有附加动量因子mc的权值和阈值调节公式为：

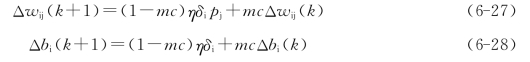
式中　k——训练次数；

mc——动量因子，一般取0.95左右。

根据附加动量法的设计原则，当修正的权值在误差中导致太大的增长结果时，新的权值应被取消而不被采用，并使动量作用停止下来，以使网络不进入较大误差曲面；当新的误差变化率对其旧值超过一个事先设定的最大误差变化率时，也应取消所计算的权值变化。其最大误差变化率可以是任何大于或等于1的值，典型取值为1.04。在进行附加动量法的训练程序设计时，必须加入条件判断以正确使用其权值修正公式。

训练程序设计中采用动量法的判断条件为：

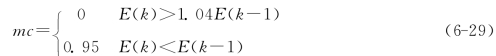
式中　E（k）——第k步误差平方和。

2.增加自适应学习速率

对于一个特定的问题，要选择适当的学习速率不是一件容易的事情。通常是凭经验或实验获取。但即使这样，对训练开始初期功效较好的学习速率，不一定对后来的训练合适。为了解决这个问题，人们自然想到在训练过程中，自动调节学习速率。通常调节学习速率的准则是检查权值是否真正降低了误差函数，如果确实如此，则说明所选学习速率小了，可以适当增加一个量；反之，则产生了过调，那么就应该减少学习速率的值。

式（6-30）给出了一个自适应学习速率的调整公式：

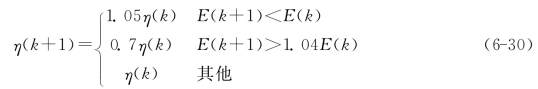
式中　E（k）——第k步误差平方和，初始学习速率η（0）的选取范围可以有很大的随意性。

6.4.3.4　结构设计

1.网络的层数确定

一般来说，增加层数可以更进一步地降低误差，提高精度，但同时也使网络复杂化，从而增加了网络权值的训练时间。而误差精度的提高实际上也可以通过增加神经元数目来获得，其训练效果也比增加层数更容易得到观察。所以一般情况下，应优先考虑增加隐含层中的神经元个数。

2.隐含层的神经元数确定

网络训练精度的提高，可以通过单个隐含层增加神经元数量的方法来获得。这在结构实现上，要比增加隐含层数要简单得多。然而，究竟选取多少隐含层节点合适在理论上并没有明确的论证。在具体设计时，比较实际的做法是通过对不同神经元数进行训练和效果对比，选取最佳的隐含层个数；另一种经验性最佳隐含层个数可由log2n（n为输入节点数）取整后确定。

3.初始权值的选取

由于系统是非线性的，初始值对于学习是否达到局部最小、是否能够收敛以及训练时间的长短有直接关系。一般希望经过初始加权后的每个神经元的输出值都接近于零，这样可以保证每个神经元的权值都能够在它们的激励函数变化最大之处进行调节。因此，初始权值的取值通常为（-1，1）之间的随机数。

4.学习速率调整

学习速率决定每一次循环训练中所产生的权值变化量。大的学习速率可能导致系统的不稳定。但小的学习速率导致较长的训练时间，可能收敛很慢，优点是能保证网络的误差值不跳出误差表面的低谷而最终趋于最小误差值。所以在一般情况下，倾向于选取较小的学习速率以保证系统的稳定性，学习速率的选取范围为0.01～0.8。