电站出力影响因子的提取和风力发电短期功率预测的统计方法

风力发电功率预测建模除了采用上述的物理方法，还可以运用多元回归、神经网络等统计学习方法。统计方法主要通过分析、提取电站出力影响要素，建立影响要素与电站发电的映射模型。电站出力影响因子的提取通常采用因子分析方法，映射模型的建立采用多元回归、神经网络等统计学习方法。

短期风力发电功率预测统计方法主要有以下步骤：

（1）收集历史气象数据、风电场运行数据，进行数据质量控制。

（2）对数据进行分析，采用因子分析方法进行模型输入因子筛选。

（3）对输入因子与功率的映射关系进行统计学习建模，检验其有效性。

（4）以因子预报值作为模型输入，实现短期功率预测。

风力发电短期功率预测统计方法建模示意图如图5-9所示。

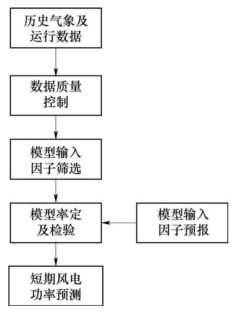
图5-9　风力发电短期功率预测统计方法建模示意图

1.数据质量控制

数据采集、通信传输会出现数据缺失或失真的现象，在模型训练时，会导致应用效果不理想。因此，在利用历史数据进行预测建模之前，首先需要进行数据质量控制，对数据进行极值检查、时间一致性检查和内部一致性检查（见本书第3章图3-15）。

在实际的建模过程中，需要考虑缺失数据的插值处理。针对少量的缺失数据可以根据数据的分布特征，采用线性插值、二次插值、拉格朗日插值等多种方法；当缺失数据较多时，可以采用临近站点数据进行插值处理。

2.模型输入因子筛选

风电场输出功率的气象影响因素主要有风速、风向、气温、气压、湿度等，若将这些气象要素直接作为统计模型的输入，会导致模型复杂度高，降低模型的鲁棒性。因此，在预测建模之前，应采用因子分析方法，提取与风电场功率输出相关性显著的输入因子。

因子分析是通过研究众多变量之间的内部关系，探求变量的基本结构，利用少数几个假想变量来反映绝大部分信息的方法。在统计建模中，气象要素是可观测的显在变量，因子分析的主要作用是基于气象要素的相关性分析，将多个气象要素包含的总信息重构到几个公共变量中，这些公共变量称之为因子。

因子分析方法具有如下优点：

（1）因子变量的数量少于原有指标变量的数量，能够减少分析中的工作量。

（2）因子变量是根据原始变量的信息进行重构，能够反映原有变量大部分的信息。

（3）因子变量之间不存在显著的线性相关关系，能够简化模型诊断分析。

因子分析方法通常用到以下关键指标：

（1）因子载荷。某个因子与某个原变量的相关系数，主要反映该公共因子对相应原变量的贡献力大小。

（2）变量共同度。对某一个原变量来说，其在所有因子上载荷的平方和就叫做该变量的共同度。变量共同度是衡量因子分析效果的常用指标，它反映了所有公共因子对该原变量的方差（变异）的解释程度。如果因子分析结果中大部分变量的共同度都高于0.8，说明提取的公共因子已经基本反映了原变量80%以上的信息，因子分析效果较好。

（3）公共因子的方差贡献。某公共因子对所有原变量载荷的平方和反映该公共因子对所有原始变量方差的解释能力，等于因子载荷矩阵中某一列载荷的平方和。一个因子的方差贡献越大，说明该因子就越重要。

对影响功率预测的潜在因素进行因子分析，其关键是以较少的几个因子反映原始数据的大部分信息。假设有p个气象因子，即p个可观测的显在变量，每个变量有n个观测值，公共变量为q个，经过归一化后的原始变量矩阵为X：

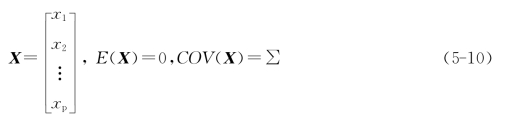
式中　E（X）——X的均值；

COV（X）——X的协方差。

因子分析需要首先计算X的相关系数矩阵R。R用来描述原始变量之间的相关关系，帮助判断原始变量之间是否存在相关性，若相关性较弱，则没有做因子分析的必要。反之，则假设公共因子变量矩阵F和特殊因子矩阵Ξ如下：

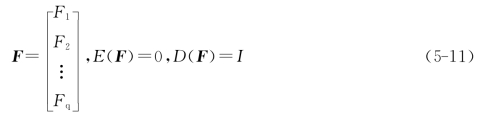
式中　E（F）——F的均值；

D（F）——F的方差。

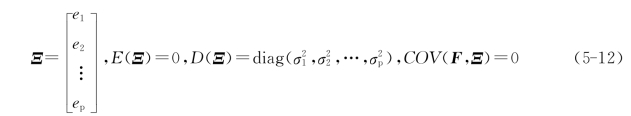
以上E（·）为期望，D（·）为方差，COV（·）为协方差，diag（·）对角矩阵。

假设

式中　A——因子载荷矩阵，A=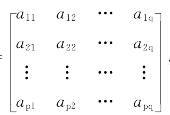，并且称aij为第i个变量在第j个公共因子上的载荷，反映了第i个变量在第j个公共因子上的相对重要性。

可以证明因子载荷aij为第i个变量xi在第j个公共因子Fj的相关系数，即反映了变量与公共因子的关系密切程度，aij越大，表明公共因子Fj与变量xi的线性关系越密切。

因子载荷矩阵中各行元素的平方和：

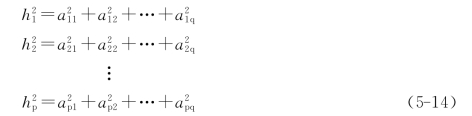
式中　、…、——变量x1、x2、…、xp的共同度，它表示q个公共因子F1、F2、…、Fq对变量xi的方差贡献，变量共同度的最大值为1，值越接近于1，说明该变量所包含的原始信息被公共因子所解释的部分越大，用q个公共因子描述变量xi就越有效；而当值接近于0时，说明公共因子对变量的影响很小，主要由特殊因子来描述。

因子载荷矩阵中各列元素的平方和：

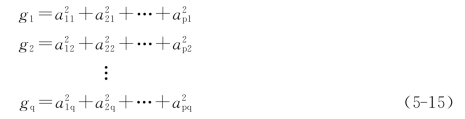
式中　g1、g2、…、gq——公共因子F1、F2、…、Fq的方差贡献。

定义Fj的贡献率为：

式中　Rj——衡量各个公共因子相对重要程度的一个指标，方差贡献率越大，该因子就越重要。(www.xing528.com)

因子载荷矩阵A的计算是进行因子分析的关键。A的求法很多，常用的为主成分法，利用相关系数矩阵R的单位特征根λ与特征向量U来构造因子载荷矩阵A的估计为：

因子分析的目的是将多个变量简化为数量较少的因子，以便进行下一步的分析，所以一般来说，公共因子的个数q要不大于变量的个数p，而且q越小越好，当p与q的差异较大时，便能将高维空间的问题降至低维空间进行处理。在实际问题中，q的数值通常可以采用不同的方法加以确定。如根据累计方差贡献率不小于85%确定，或者根据大于1的特征根来确定。

当获得公共因子和因子载荷后，我们可以进一步计算每一个样本点在每一公共因子上的得分，从而对样本点进行评价、排序、比较和分类。计算因子得分先要根据因子分析建立每个因子的回归方程，然后以原始变量为回归目标，求出因子分数。一般常用的方法有回归法、巴特利特方法和Anderson-Rubin法等。估计因子得分函数的常用方法是回归法，因子的得分估计为：

综上所述，利用因子分析对短期预测输入元素进行重构的主要步骤为：

（1）原始数据标准化。

（2）建立相关系数矩阵R，求R的单位特征根λ与特征向量U。

（3）根据A=求因子载荷矩阵A。

（4）建立因子模型X=AF+E。

（5）计算因子得分。

3.统计学习

统计学习的目的是建立输入影响因子与风电场输出功率之间的对应关系，根据应用场景和应用数据，可以采用多种方法。下面就常用的多项式拟合、多元回归、神经网络进行介绍。

（1）多项式拟合。当模型输入因子为单个的时候，可以采用多项式拟合建立因子与功率输出之间的关系。多项式拟合又称为函数逼近，是求近似函数的一种数值方法。多项式拟合的主要作用是寻找一个多项式函数y=p（x），使得训练样本集的拟合值与实测值在某种准则下最接近，一般采用的准则为离差平方和最小，多采用最小二乘法进行估计。

多项式拟合的一般方法可归纳为以下几步：

1）根据数据散点图初步确定拟合多项式的阶数n。

2）利用最小二乘法率定多项式系数a0，a1，…，an。

3）求出拟合多项式pn（x）=。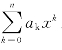

当有多个输入因子的时候，多项式拟合就不足以用来学习输入因子与功率输出之间的关系，这时常采用的方法为多元回归与人工神经网络。

（2）多元回归。假设风电场输出功率为随机变量y，影响y的因子有x1，x2，…，xp，则线性回归模型为：

写成矩阵形式为：

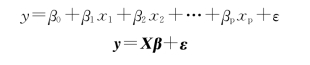
其中

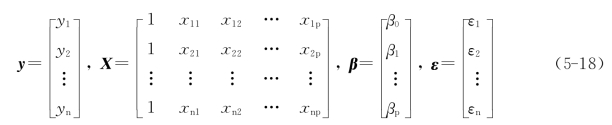
解释变量x1，x2，…，xp是确定性变量，不是随机变量，样本容量的个数应大于解释变量的个数，X是一满秩矩阵。同时要求随机误差项均值为0、方差为常数，即：

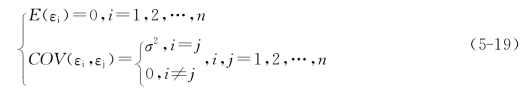
E（εi）=0，即假设观测值没有系统误差，随机误差εi的平均值为0；随机误差εi的协方差为0表明随机误差项在不同的样本点之间是不相关的，不存在序列相关，并且具有相同的精度，经过因子分析处理的输入因子可以达到要求。正态分布的假定条件为：ε～N（0，σ2In）。由该假定和多元正态分布的性质可知，随机变量y服从n维正态分布，y～N（Xβ，σ2In）。回归系数β的估计值可以由常用的最小二乘法或者极大似然估计法给出。

采用多元回归进行短期功率预测，预测结果为电场短期出力期望值的估计。需要注意的是，由于功率与输入因子之间并不一定呈线性关系，可以将输入因子或者功率进行变换后再利用多元回归进行建模，如xi可以为某原始输入因子的平方，y可以为功率的自然对数等，这样可以利用多元回归对非线性关系进行学习。

（3）神经网络。人工神经网络（Artificial Neural Networks，ANN）是一种模仿动物神经网络行为特征进行分布式并行信息处理的数学模型。人工神经网络模型主要考虑神经元的特征、网络连接的拓扑结构、学习规则等。神经网络通过调整内部大量节点之间相互连接的关系，从而达到处理信息的目的。人工神经网络具有自适应学习的能力，是对动态的、复杂的、非线性的数据进行分析的有效手段。

神经元是构成神经网络的最基本单元，对于每一个人工神经元来说，它可以接受一组来自系统中其他神经元的输入信号，每个输入对应一个权，所有输入的加权和决定该神经元的激活状态。这里，每个权就相当于突触的“联接强度”。设人工神经元i的n个输入分别用x1，x2，…，xn表示，它们对应的联接权值依次为ωi1，ωi2，…，ωin，用net来表示该神经元所获得的输入信号的累积效果，称为网络输入。

神经元在获得网络输入后，它应该给出适当的输出。按照生物神经元的特性，每个神经元有一个阈值，当该神经元所获得的输入信号的累积效果超过阈值时，它处于激发态；否则，应该处于抵制态。为了使系统有更宽的适用面，希望人工神经元有一个一般的变换函数，用来对该神经元所获得的网络输入进行变换，这就是激活函数，也可称为激励函数或者转换函数。用f表示：

式中　yi——该神经元的输出。

由此式可以看出，函数f同时也用来将神经元的输出进行放大处理或限制在一个适当的范围内。典型的激活函数有符号函数、阶跃函数、S型函数等。

将大量的神经元进行联接可构成人工神经网络。神经元之间的连接方式不同，可得到不同的神经网络，根据联接方式不同，我们可以简单将神经网络分为两大类：无反馈的前向神经网络和相互连接型网络（包括反馈网络），前向神经网络和反馈型神经网络分别如图5-10和图5-11所示，用圆圈简单表示图中的神经元。前向神经网络分为输入层、隐含层和输出层，各个层所含神经元数量可以不同。隐含层可以有若干层，每一层的神经元只接收前一层神经元的输出。而相互连接型网络的神经元相互之间都可能有连接，因此，输入信号要在神经元之间反复往返传递，从某一初态开始，经过若干次变化，渐渐趋于某一稳定状态或进入周期振荡等其他状态。

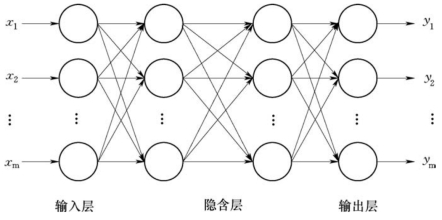
图5-10　前向神经网络

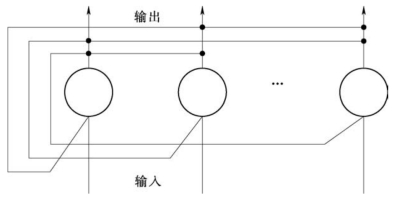
图5-11　反馈型神经网络

各神经元之间连接强度是由神经网络内部加权系数决定的，加权系数决定了信号传递的强弱，信号可以起刺激作用也可以起抑制作用，而且加权系数可以随着训练进行改变。这些特征使得人工神经网络具有高度的灵活性。

神经网络的学习过程是修改加权系数的过程，使其输出接近或达到期望值。学习算法是神经网络的主要特征，也是当前研究的主要课题。神经网络学习算法很多，常用的有Hebb学习算法、Widrow-Hoff学习算法、反向传播（Back Propagation）学习算法、Hofield反馈神经网络学习算法、竞争（Competitive）学习算法、按照自适应谐振理论构成自组织神经网络学习算法等。

神经网络的学习方式可分为无导师学习和有导师学习。无导师学习又称为非监督学习（Unsupervised Learning），它不需要目标，其训练集中只含一些输入向量，训练算法致力于修改权值矩阵，以使网络对一个输入能够给出相应的输出，即相似的输入向量可以得到相似的输出向量，Hebb学习规则是最早被提出的无导师学习算法。有导师学习又称为监督学习（Supervised Learning），要求用户在给出输入向量的同时，还必须同时给出对应的理想输出向量（期望输出）。有导师训练算法中，最为重要、应用最普遍的是Delta学习规则（纠错学习规则）。

4.模型检验

模型检验是使用统计方法进行功率预测建模过程中的一项重要环节。在已有实测数据及模型输出数据的前提下，通过比较模型输出和实测数据，对模型有效性进行定量分析，如果模型输出与实测数据类似，则认为该模型有效。

模型检验主要包括理论模型有效性确认、数据有效性确认和运行有效性确认三个部分。理论模型有效性确认主要检验模型的理论依据、假设条件的正确性和模型结构的合理性，检验可以采用统计方法实现；数据有效性确认包括对模型中关键变量、关键参数及随机变量的检查，保证模型在建立、评估、实验过程中所用的数据充分准确；运行有效性确认是对模型输出结果的精度进行计算和评估。