数值天气预报误差校正实例

为了验证模式误差订正算法的有

效性，本书对数值天气预报的风速和地表总辐射分别采用卡尔曼滤波法和自适应偏最小二乘法进行模式误差订正，并进行了对比分析。

（1）风速预测模式误差订正。选取华东沿海地区的一个风电场作为验证现场，对风速预报的模式误差进行订正，使用的数据为WRF模式70m高层风速预报结果和测风塔70m高层风速测量数据，时间为2012年10月1日至12月31日。选取总样本50%的数据进行模型训练，剩余数据用于模型验证。图4-9和图4-10显示了风速实测、原始预测以及偏最小二乘法和卡尔曼滤波订正的预测结果对比。

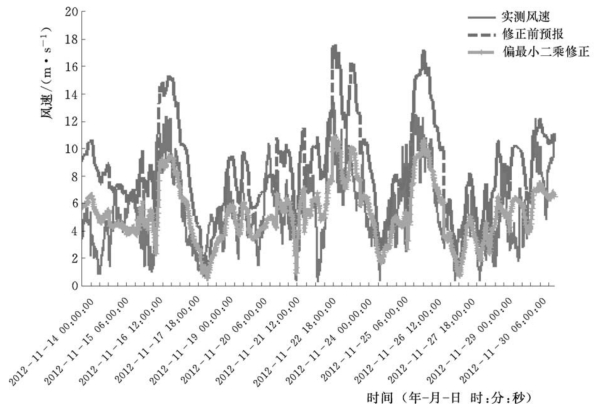
图4-9　风速实测、原始预测和偏最小二乘法订正结果对比

数据统计表明，原始预测均方根误差为3.91m／s，平均绝对误差为3.25m／s；采用自适应偏最小二乘法进行校正后的均方根误差为2.06m／s，平均绝对误差为1.67m／s；采用卡尔曼滤波法进行校正后的均方根误差为2.62m／s，平均绝对误差为2.08m／s。由图4-9和图4-10可见，原始风速预测结果整体偏大，特别在风速出现峰值的时段，预测绝对误差可达到5m／s。采用自适应偏最小二乘法和卡尔曼滤波法订正后，预测结果有了明显改善，其中自适应偏最小二乘法倾向于将整体风速订正到平均值附近，而卡尔曼滤波法在初始时误差较大，随着模型训练时间的增加，误差逐渐减小，显示了较好的跟随性，但在某些波动较大的时段订正效果较差。

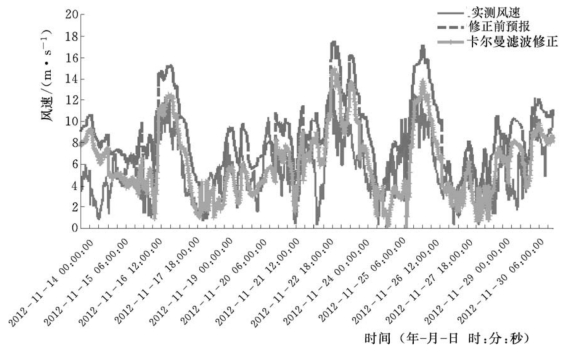
图4-10　风速实测、原始预测和卡尔曼滤波订正结果对比(www.xing528.com)

（2）地表总辐射预测模式误差订正。地表总辐射的模式误差订正，选取了甘肃省的一个辐射观测站2012年11—12月的数据进行分析，去除无效时段，训练数据和验证数据集选用9：00—19：30之间的时间段。

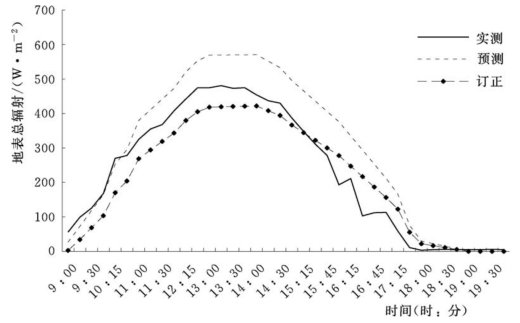
图4-11　地表总辐射实测、原始预报和自适应偏最小二乘法订正结果对比

图4-11为采用自适应偏最小二乘法的订正结果与实测、原始预报结果的对比。其中，预报值与实测值间相关系数为0.96，均方根误差为88W／m2，平均绝对误差为71W／m2。从预报与实测曲线对比可见，预报值普遍大于实测值。经过自适应偏最小二乘法订正以后，订正值的相关系数为0.97，均方根误差为52W／m2，平均绝对误差为44W／m2。对比订正前后的误差，均方根误差降低了36W／m2，平均绝对误差降低了27W／m2，预测误差得到显著降低。结合12月1日实测、预测和订正结果对比图不难发现，订正后的预测曲线与实测值曲线更加吻合，但订正值较实测值相对偏小。

图4-12为采用卡尔曼滤波法，选择同样的数据集与实测和原始预报得到的结果对比。经过卡尔曼滤波法订正以后，订正值的相关系数为0.99，均方根误差为40W／m2，平均绝对误差为29W／m2。对比订正前后预报值可知，订正后精度明显提升，均方根误差降低了48W／m2，平均绝对误差降低了42W／m2。

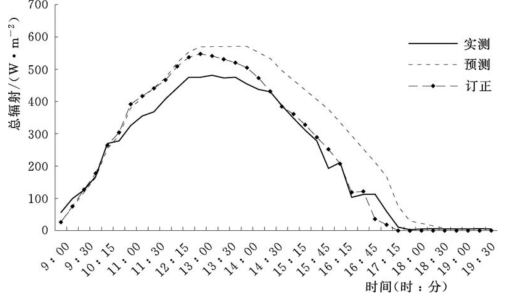
图4-12　地表总辐射实测、原始预报和卡尔曼滤波订正结果对比

与自适应偏最小二乘法对比，卡尔曼滤波法在11：00—14：00之间存在正误差，之后的订正曲线就基本贴合实测辐射，而自适应偏最小二乘法从9：00—15：00之间呈现负误差，之后转为正误差，这说明卡尔曼滤波法能够逐步调整订正结果，使得误差达到最小，而自适应偏最小二乘法则是对预报结果进行整体订正，导致局部订正效果较弱。