卡尔曼滤波：智能优化方法

卡尔曼滤波法是一个最优化自回归数据处理算法，其应用历史已经超过30年，在包括机器人导航、控制、传感器数据融合，甚至在军事方面的雷达系统、弹道追踪等方面均有广泛应用。近年来卡尔曼滤波法更是被广泛应用于计算机图像处理和数值计算中。

卡尔曼滤波法简单来说是一种有效的以最小均方误差来估计系统状态的计算方法，即通过将前一时刻预报误差反馈到原来的预报方程中，及时修正预报方程系数，以提高下一时刻的预报精度。在卡尔曼滤波算法中，描述系统的数学模型是状态方程和观测方程，分别为

式中　xt——未知过程在t时刻的状态向量；

yt——t时刻的观测向量；

Ft，Ht——系统矩阵及观测矩阵，且必须在滤波器应用之前确定；

wt，vt——系统噪声和观测噪声，均假定为高斯白噪声且相互独立。Wt，Vt为与系统噪声和观测噪声相对应的协方差矩阵。

卡尔曼滤波算法提供了一种在观测向量更新为yt的基础上，运用递归来估计未知状态的算法。

假定现有系统状态为xt，则在上一状态xt-1及其协方差矩阵Pt-1的基础上，可以得到t时刻的预报状态及其协方差矩阵的预报方程，即

(www.xing528.com)

当新的观测向量yt更新后，就可以得到t时刻的状态向量xt的最优估计，即

式中　Kt——卡尔曼增益，为卡尔曼滤波算法的重要参数。

Kt计算公式为：

至此，可以更新未知状态xt在t时刻的协方差矩阵，并作为算法递归运行的条件，即

以上公式称为卡尔曼滤波器的更新方程，图4-8为卡尔曼滤波流程示意。

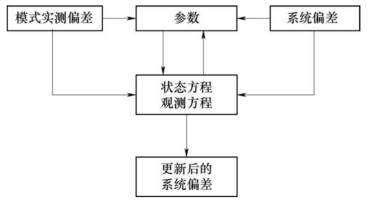
图4-8　卡尔曼滤波流程示意图