基于机动目标硬件状态的估计方法优化

目前常采用的目标状态估计方法，都可以采用贝叶斯框架进行统一描述，也正是由于贝叶斯方法在描述不确定性方面的独特优势，在统计推理等科学和工程领域得到了广泛的应用。已经成为目标跟踪、故障诊断、导航定位、过程优化、模型控制等问题的标准解决方法。传感器检测到新的信息后，贝叶斯方法融合前一时刻的状态估计和当前的测量更新状态，在时间上更新过程是递归的。

1.递推贝叶斯估计

概率贝叶斯方法以概率分布的形式实现非线性系统的状态估计，将状态估计问题看作概率推理过程，即根据所有测量信息 Yk={y1，y2，…，yk}计算状态 xk的后验概率密度 p（xk|Yk）。在后验概率密度计算过程中，还囊括了所有关于状态矢量xk和关于xk-1先验分布的信息，一旦后验分布确定，就可以得到状态的最优估计。即状态 xk或相关函数 f（xk）的估计可以由条件期望给出：

贝叶斯理论是计算后验分布的基础，而递推贝叶斯估计基本上符合序贯贝叶斯滤波的原理。在推导贝叶斯滤波时，需要满足两个前提假设：状态转移符合马尔科夫过渡过程 p（xk|x0 ：k-1）=p（xk|xk-1）；给定状态的观测是独立的。根据贝叶斯规则：

后验概率密度 p（xk|Yk）主要由三项构成：

·先验（Prior）：概率预测方程或Chapman-Kolmogorov（CK）方程

式中，p（xk|xk-1）是状态转移密度。

·似然（Likelihood）：似然 p（yk|xk）确定测量噪声模型。

·证据（Evidence）：分母涉及一个积分

上述三项的计算和近似是贝叶斯推理和滤波最基本的操作，主要包括预测和更新两步操作。图5-73给出了贝叶斯估计的结构框图。从上述贝叶斯推理过程可以看出，递推贝叶斯估计需要计算积分，除了线性高斯、有限状态的离散等特殊的系统外，只有概率密度函数的所有矩都计算在内，才能完整刻画概率密度函数。对于一般的非线性、非高斯系统，很难得到准确的闭合解析解，必须采用近似的方法计算无限维上的积分问题，从而得到状态估计的次优解。

2.最优线性滤波

（1）最小方差估计

最小方差估计主要解决线性测量的状态估计问题，状态矢量可以采用如下噪声模型描述：

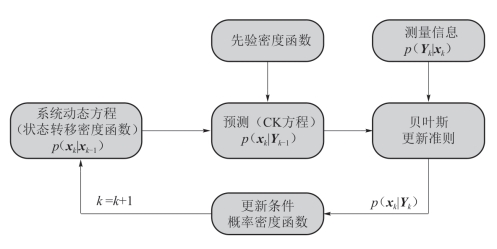
图5-73　贝叶斯估计的结构框图

其中，测量噪声 v∈Rm×1，均值为零，其方差R∈Rm×m；H∈Rm×n，为状态 x∈Rn×1与测量y∈Rm×1之间的线性映射矩阵。

当测量存在冗余信息时，即 m＞ n，根据最小方差原理，状态x 可以通过最小化误差损失函数得到其最优估计：

损失函数表示为矢量形式：

将损失函数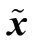的微分等于零，得到最小方差估计，因此

必要条件：

充分条件：

式中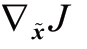，为Jacobian 矩阵；为Hessian 矩阵。由必要条件可得到状态的最优估计：

式（5-90）给出的最小方差估计中，所有的测量的权重均相同。而在实际应用中，每个测量的精度、置信度等都可能存在差异，为此，可以将损失函数加权，即加权最小方差估计算法：

同上述推理，根据必要条件可得加权最优估计为：

由上述分析可以看出，最小方差估计器没有任何概率假设和相关的解释，而是完全从确定的观点求解的，因此，在没有任何关于状态和量测的概率密度函数信息时非常实用。从另外一个角度讲，当测量噪声符合均值为零，方差为Rii的独立高斯分布时，最小方差同最大似然（ML）是等价的。

式中，c 为大于零的常数；yk表示到k 时刻的所有测量，yk=[y1，y2，…，yk]T。要使似然函数 p（yk|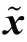）最大，则式（5-92）中指数项最小，因此最小方差和最大似然的结果一致。

当状态和观测矢量概率密度函数的统计模型已知时，可以采用贝叶斯估计的方法求解，问题也就转换成后验密度函数p（x|y） 的求解问题。根据最优标准准则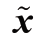，可以根据后验概率估计。换句话说，贝叶斯估计可以通过最小化风险函数J 实现。

式中，p（x，y）为随机变量x 和y 的联合密度函数；损失函数 J（Δx）是关于估计误差Δ x=x-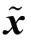的函数。由最小化风险函数J 可得条件均值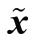为：

假定状态和噪声都符合高斯分布，则条件均值可以表示为：

式中，P0 是x 的先验协方差矩阵。可以看出，如果没有先验信息，式（5-94）就简化成式（5-91）。由此可见，贝叶斯估计完全可以涵盖最小方差估计，最小方差只不过是贝叶斯估计的一个特例。

（2）卡尔曼滤波

20世纪60年代，卡尔曼把状态空间模型引入滤波理论中，并构建了一套递推估计算法，即卡尔曼滤波理论。对于线性高斯系统，卡尔曼滤波可以得到最小均方误差意义下的最佳估计。其基本思想是：采用信号与噪声的状态空间模型，利用前一时刻的估计值和现在时刻的观测值更新状态变量的估计。

给定的线性系统为：

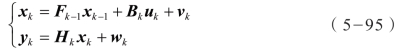
假定动态系统和测量噪声相互独立，wk和 vk都是零均值高斯随机变量，协方差分别为 Qt 和 Rt。初始状态是均值为E [x1]，协方差为 Cov（x1）的高斯矢量。当n＞1时，KF 可以由两个矢量描述：

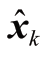：k 时刻给定观测后的状态估计；

Pk：由 xk-确定的误差协方差矩阵。

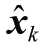中包含了k 时刻的观测信息，协方差矩阵 Pk 描述了k 时刻的不确定性。KF 算法采用预测和更新两步操作完成状态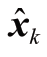和协方差 Pk 的估计，图5-74给出了相应的估计流程。

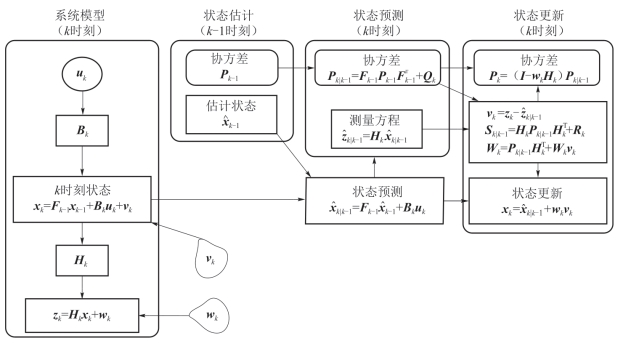
图5-74　卡尔曼滤波预测-校准过程

在线性、高斯条件下，卡尔曼滤波器是无偏的最小方差估计器。当噪声不符合高斯分布时，卡尔曼滤波在均方差意义下仍然是最优，但可能有偏估计且不是最小方差。由于对噪声密度模型有前提假设，因此卡尔曼滤波算法鲁棒性较差。

对于被零均值高斯噪声污染的线性过程模型，采用卡尔曼滤波方法可以得到最小方差意义下的最优估计。主要是由于高斯信号经过线性系统变换后，仍然为高斯分布，且两个独立的高斯随机变量之和仍然符合高斯分布。然而，当经过非线性变换后，高斯分布就不再保持该特性了。

通常情况下，噪声测协方差被认为是常量，在某些情况下可能是变化的，因此需要进行调整。在实际应用中，在滤波之前需要测量噪声的协方差，但在滤波过程中，噪声的协方差有时是变化的。

状态转换噪声方差更难确定，有时如果充分考虑系统的不确定性，即便是较差的模型，也可能得到比较理想的结果。无论哪种情况，协方差都需要进行调整。通常情况下采用另外一个卡尔曼滤波器离线完成。

3.非线性状态估计

对于过程和观测噪声都是高斯分布的线性系统，KF 可以得到最优的闭式解。而在实际应用中，卡尔曼滤波由于受线性、高斯条件约束，其应用受到很大的限制。因此，自卡尔曼滤波方法发表以来，以KF 为基本框架提出了很多改进的滤波算法，解决非线性、非高斯问题，这些方法都是根据已知的量测信息确定系统状态矢量的概率密度分布的，因此可以采用统一的贝叶斯框架描述。

由于非线性系统需要无限维的过程处理，递归贝叶斯问题的最优准确解则不可得，因此，提出了众多非线性滤波的近似解法。根据近似方式不同，可以分成5 种类型：① 解析近似方法；② 直接数值近似方法；③ 确定的采样方法；④ 高斯混合滤波器；⑤ 基于仿真的滤波方法。

（1）解析近似方法（EKF）

如前所述，KF 滤波器只有在系统为线性、噪声为高斯白噪声时才能得到最优估计。为了充分发挥KF 滤波的特点来解决非线性问题，通常需要对非线性函数线性化近似。扩展卡尔曼滤波器（EKF）级采用一阶泰勒级数对非线性系统近似，是目前使用最为广泛的非线性滤波方法。EKF 在当前均值和方差附近对系统模型线性化，根据状态模型和观测模型的统计特性，给出状态的最小方差估计，属于解析近似的方法之一。

给定的非线性系统

式中，初始状态 x0和初始协方差 P0 为已知或预先估计得到；状态转换噪声 vk和观测噪声wk为零均值的高斯噪声；方差Qk和 Rk 为已知。

EKF 方法估计的每一步都在当前估计点附近对系统模型线性化，并假定噪声为零，则定义：

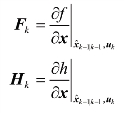
估计的每一步都需要计算上述Jacobian 矩阵，然后采用卡尔曼滤波器对线性化以后的模型进行估计，因此有：

预测：

更新：

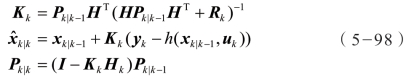
EKF 滤波器预测-校准过程如图5-75所示。

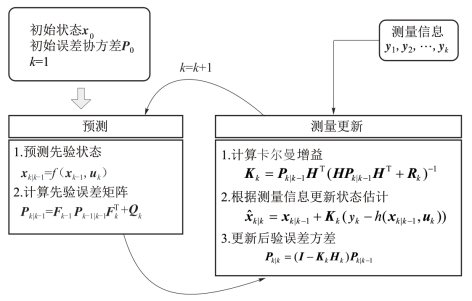
图5-75　EKF 滤波器预测-校准过程

扩展卡尔曼滤波器在当前估计点对系统进行简单的线性化，均值和协方差的传递更新都是通过一阶泰勒级数线性化更新的，而对于高阶非线性系统，简单的线性化会产生很大的误差，有时甚至会发散。经过非线性变换后，随机变量不再是正态分布，此种影响会随着估计步数的递增而递增；在线性化过程中，非线性可观测过程可能会变成不客观，从而使校准性能变差，如果局部线性化误差较大，线性化可能会导致滤波器不稳定。此外，在实际应用中，很多问题的非线性函数的Jacobian 矩阵求导非常困难，有些系统甚至不存在。

（2）确定的采样方法

EKF 采用泰勒级数展开，对非线性系统线性化的过程中忽略了高阶项，也就意味EKF 是有偏的，并且往往会低估状态估计的协方差水平。有文献在EKF 算法中引入了二阶项，一定程度上提高了估计精度，但仍然没有克服其固有缺陷。无迹卡尔曼滤波器（UKF）采用选择状态点通过模型传播的方式实现了非线性函数的概率密度分布的近似。由于近似概率密度分布要比近似非线性函数本身容易，因此，基于采样方法的非线性分布近似策略在解决非线性状态估计问题时更具优势。

UKF 以UT 变换为基础，采用标准卡尔曼滤波架构实现非线性系统状态的预测和更新。UT 变换是一种确定的采样近似方法，通过采样近似状态的均值和方差等统计特性，其采样点通常被称为Sigma 点。UT 变换在某种程度上和点云相同，都是使用Sigma 点和相应的偏移参数传递数据信息。UKF 滤波器算法与EKF 算法相比，计算量基本相当，但精度通常可以达到二阶，且不需要计算Jacobian 矩阵。采用确定性的采样策略，规避了PF 算法的粒子蜕化问题。

UT 变换采用确定采样方法计算状态的均值和方差，并基于近似概率分布比近似非线性函数本身容易的原理实现了统计特性的非线性传递。nx维随机变量x 经过非线性函数g 作用后产生y，Y=g（χ）。假设已知x 的均值 x0 和方差 Px，产生2nx+1个Sigma 点，以便计算均值和方差，具体如下：

式中，κ 为比例参数；为（nx+κ）Pxx的第i 行矩阵方根；Wi 为第i 个采样点相关的权重。(www.xing528.com)

均值和方差传递原理图如图5-76所示。

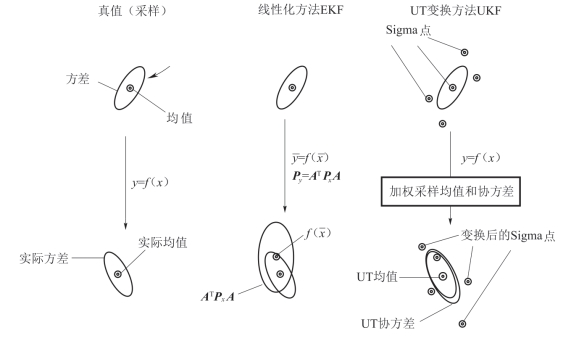
图5-76　均值和方差传递原理图

Sigma 点经过非线性函数 g：Yi=g（χi），i=0，1，…，2nx 作用后，均值和方差估计为：

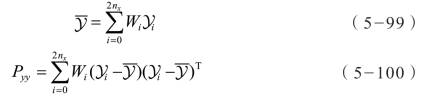
对任何非线性函数和分布，上述估计可以达到 g（x） 的二阶泰勒级数展开的精度，然而，在某些情况下，协方差矩阵可能是非正定的，计算矩阵的均方根引起协方差矩阵的病态问题。尽管正则化和方根UKF 能够一定程度上缓解此类问题，但是为了提高算法的鲁棒性，有学者提出了采用奇异值分解（SVD）的方法计算。之所以采用SVD 分解代替特征值分解，完全是因为SVD 在数值计算上更稳定。

为了将UT 变换用于卡尔曼滤波器中，将状态转换和测量噪声增广到状态变量中，状态转换和测量噪声的协方差增广到状态协方差矩阵：

根据增广的状态和协方差计算Sigma 点。

必须计算Sigma 点并经过状态转换模型预测新的状态，因此需要对预测进行扩展。而预测的状态也必须通过测量模型变换，以便预测测量状态。具体描述如下：

式中，Sigma 点为：

经过状态转换模型变换Sigma 点：

预测下一步状态：

预测协方差矩阵：

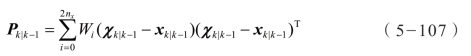
通过测量模型变换Sigma 点：

预测测量值：

预测测量方差：

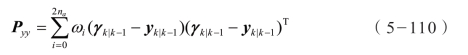
状态更新和卡尔曼滤波器相同。

计算卡尔曼增益：

校准预测状态：

校准协方差：

UKF 滤波器预测和更新操作流程如图5-77所示。

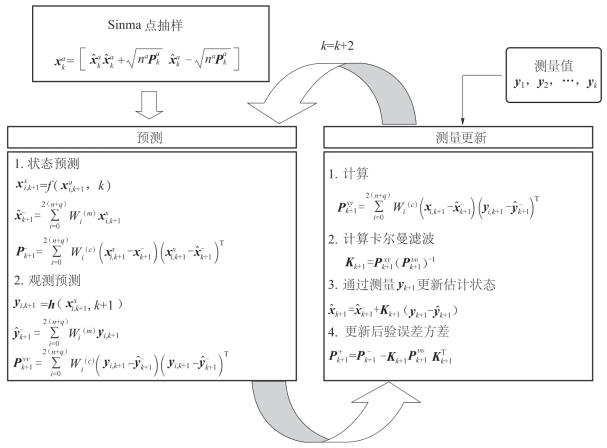
图5-77　UKF 滤波器预测和更新操作流程

UKF 算法采用确定性采样的方法计算均值和方差，能够克服EKF 固有的缺点。特别是产生（2 nx+1）个Sigma 点并经过非线性传递后，可以进一步计算均值和方差。和一阶EKF 估计精度相比，对于高斯分布数据，UKF 的估计精度可以达到三阶；对于非高斯分布数据，至少可以达到二阶。类似的方法还有均差滤波器（Divided Difference Filter，DDF）、积分卡尔曼滤波器（Quadrature Kalman Filter，QKF）、中心差分滤波器（Central Difference Filter，CDF）、高斯埃尔米特滤波器（Gaussian-Hermite Filter，GHF）等，这些算法统称为Sigma 点卡尔曼滤波（Sigma-point Kalman Filter，SPKF）。DDF 和CDF 都是使用Sterling 多项式公式近似非线性系统，均值和方差均由Sigma 点确定，同时与KF 结合，进而实现对非线性函数的近似，而QKF 算法采用Gaussian-Hermit 积分规则，从线性回归的角度计算递归贝叶斯积分，并通过选取高斯点作为Sigma 点实现近似变换，克服了线性可微的限制。GHF 算法是一种基于Gaussian-Hermite 数值积分的贝叶斯滤波算法，该算法通过选取高斯点和相应的权重来提高系统均值和方差的估计精度。EKF 和上述所有Sigma 点滤波算法都是针对当前状态对非线性模型进行评估的，但Sigma 点滤波算法不需要计算Jacobian 矩阵，且精度明显高于EKF 算法。

图5-78给出了EKF、Sigma 点滤波算法和PF 的采样方式原理。从广义上讲，UKF 属于PF 的一种特殊形式，都是利用一系列从概率密度中得到的采样点完成序贯估计。区别在于UKF、DDF、QKF、CDKF、GHF 等Sigma 点滤波算法假定过程和量测噪声符合高斯分布，从而简化了递归贝叶斯估计。粒子滤波算法可以处理非线性模型和非高斯分布，更为通用。

4.粒子滤波算法

在过去十几年中，粒子滤波在众多领域取得了广泛的应用，主要包括视觉跟踪、语音识别、移动机器人定位、导航、故障诊断。粒子滤波算法与传统滤波方法及确定性采样估计方法相比，粒子滤波算法采用加权的随机采样粒子，能够描述任意概率密度函数，可以解决非线性、非高斯的状态估计问题。

粒子滤波实质上是采用随机采样描述概率分布，然后根据测量信息通过调整粒子的权重大小和采样位置，实现概率分布的近似，最终以样本的均值作为系统的状态估计。因此，粒子滤波算法主要包括三步重要操作：产生粒子；计算粒子权重；重新采样。前两步构成序贯重要采样方法（SIS），SIS 滤波算法加上重采样构成了通用的粒子滤波算法。

（1）蒙特卡罗采样

蒙特卡罗方法采用统计采样和估计技术确定数学问题的解。蒙特卡罗方法主要包括三类：蒙特卡罗采样、蒙特卡罗计算、蒙特卡罗优化。在近十年中，蒙特卡罗方法得到了越来越多的关注，且在不同领域得到了应用，本节主要总结与PF 相关的MC 采样方法。考虑估计Lebesque-Stieltjes 积分问题：

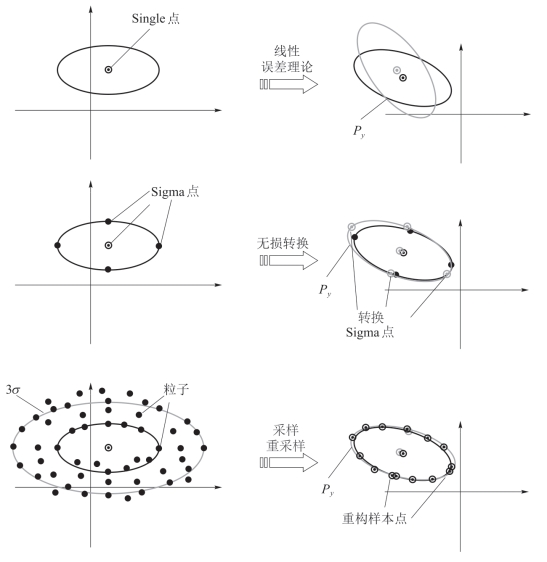
图5-78　EKF、UKF、PF 采样方式对比

式中，f（x）是在可测量空间内的可积分函数。

蒙特卡罗采样在概率空间（Ω，F，P）内采用随机变量近似积分，假定从概率分布 P（x）中随机抽取Np个点序列 {x（1），x（2），…，x（Np）}，则 f（x）的蒙特卡罗估计可以表示为：

根据Kolmogorov 强大数定理，一定能够收敛到 E[f（x）]，且其收敛速度可以采用中心极限定理确定：

式中，σ2是 f（x）的方差，误差的收敛速度为，同一维积分相比，比收敛速度要慢。但是蒙特卡罗近似方法的一个显著特征就是估计精度与状态空间的维数无关，估计的方差和采样数量成反比。

在蒙特卡罗采样方法中，有两个基本问题需要解决：一个是如何从概率分布P（x） 中随机抽取采样点{x（i）}，另外一个是如何估计函数的期望，即分布或密度函数。第一个问题是设计问题，而第二个问题则涉及积分的推理问题，PF 算法需要同时解决这两个问题。

（2）序贯性重要采样滤波（SIS）

对于非线性系统，且假定过程和量测噪声相互独立，系统的状态是马尔科夫过程。由于模型既非线性也非高斯，后验分布只能采用全部的概率密度函数描述。递归马尔科夫模拟采用随机的方法可以估计，递归方程为

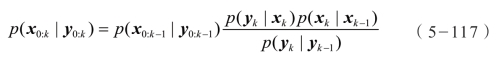
在粒子滤波算法中，为了避免贝叶斯估计的积分计算，后验分布或密度采用后验分布Np 个采样的加权和方式表示：

式中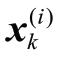，表示从 p（xk|Yk）中抽取的独立同分布随机变量，当Np足够大时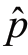，（xk|Yk）能够近似实际的后验分布 p（xk|Yk），从而可以得到关于状态变量的非线性函数 f（xk）的均值和方差：

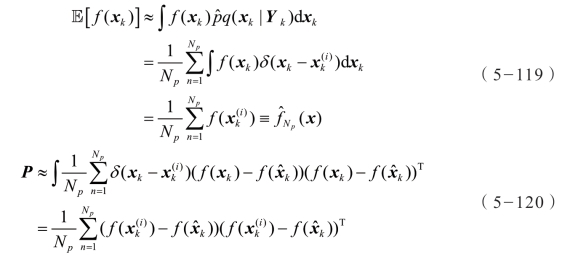
通常情况下，后验分布未知或很难进行采样，因此，一般从给定的相对较容易的分布中采样，即所谓的提议分布，定义为 q（xk|Yk）。

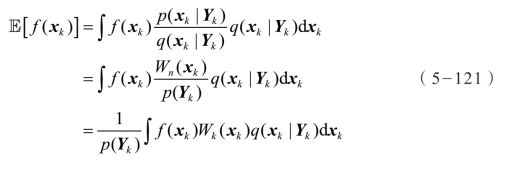
式中

方程（5-44）可以表示为：

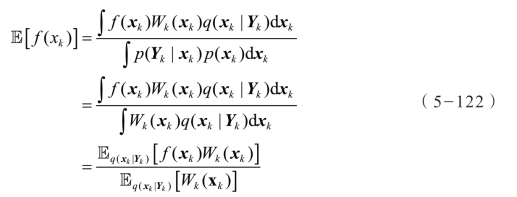
通过从 p（xk|Yk）中获得独立同分布随机变量 {}，可以得到相应的函数及其协方差估计：

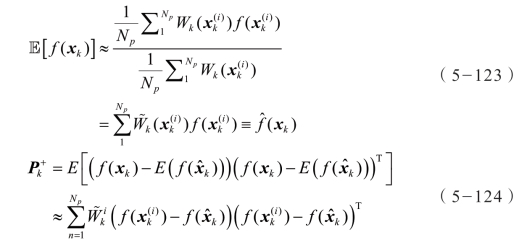
式中

假定提议分布有如下分解形式：

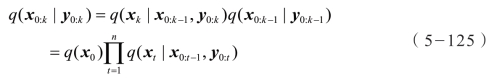
因此，重要性权重 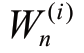可以根据下式递归更新：

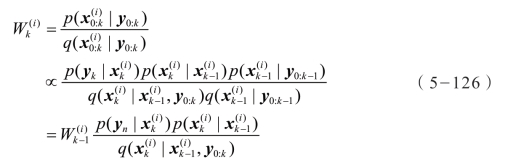
SIS 滤波器的问题在于随着时间的增加，重要性权重的分布越来越集中。因此，经过多次迭代后，只有少量的粒子的权重不为零，也就意味着绝大多数粒子对于状态估计没有贡献。该现象被称为权重蜕化（Weight Degeneracy）。最直接的解决办法就是繁殖具有高权重的粒子，摒弃低权重的粒子，即为重采样操作。图5-79给出了带有重要性采样和重采样的通用粒子滤波算法的示意图，表5-6给出了相应的算法。

图5-79　带有重要性采样和重采样的通用粒子滤波示意图

表5-6　标准粒子滤波算法

（3）重采样

为了监测权重蜕化的情况，引入了有效粒子数Neff 参数：

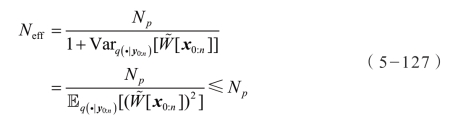
上述方程的第二个等式利用了Var[ξ]=E[ξ2]-（E[ξ]）2和 Eq [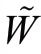]=1两个条件。实际上，其并不能够计算出真正的Neff 参数，因此可以采用其估计Nˆeff 代替：

当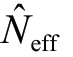小于预先定义的阈值Nth（如Nth等于 Np/2或Np/3）时，启动重采样操作。重采样的方法很多，主要包括残差重采样（Residual Resampling）、分层重采样（Stratified Resampling）、系统重采样（Systematic Resampling）、多项式重采样（Multinomial Resampling）、最小方差采样（Minimum Variance Sampling）、正则化重采样（Regularized Resampling）及基于马尔科夫链蒙特卡罗的重采样方法等。