目标机动性建模方法

对于非合作目标，其运动状态存在诸多不确定性，尤其是高机动作战条件下，这种不确定性更为突出。而这种不确定性对目标跟踪和火控系统弹道解算会带来直接影响。图5-72给出了匀加速直线运动目标的解命中预测误差。

在实际应用中，在充分考虑目标运动特点的基础上，一般选择相对简单的模型描述目标的状态转移特性。根据目标的机动状况，一般分为两大类：一类是非机动目标模型，主要有匀速直线运动（Constant Velocity，CV）模型、匀加速运动（Constant Acceleration，CA）模型和协同转弯运动（Coordinate Turn，CT）模型；另一类是机动目标模型，主要有一阶时间相关模型（Singer 模型）和“当前”统计模型。此外，为了更加准确地描述目标运动状态，还可以采用二阶马尔科夫加速度模型、交互式多模型、参数辨识模型等，本节简要介绍几种常用的目标运动模型。

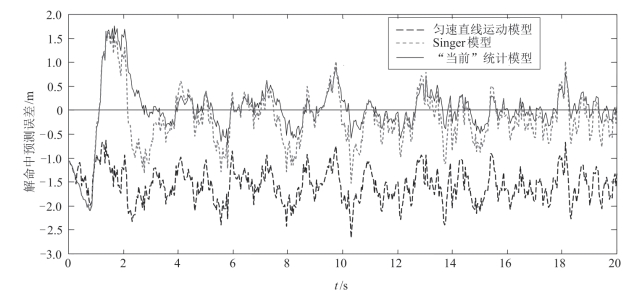
图5-72　匀加速直线运动目标的解命中预测误差

1.CV 模型

假设目标做匀速直线运动，目标的状态向量可以采用 sk=（xk，vxk，yk，vyk）T，其中，（xk，yk）表示目标的位置，（vxk，vyk）表示目标的速度。对于被跟踪的目标，其状态转移方程可以采用如下形式描述：

式中，Fk 为状态转移矩阵；Gk 为噪声输入矩阵。

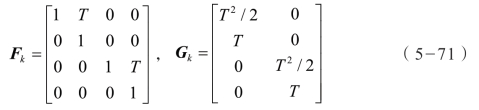
式中，T=tk-1-tk为系统采样时间。

2.CA 模型

假设目标做匀加速直线运动，目标的状态向量可以采用sk=（xk，vxk，axk，yk，vyk，ayk）T，其中，（xk，yk）表示目标的位置，（vxk，vyk）表示目标的速度，（axk，ayk）表示目标的加速度。对于被跟踪的目标，其状态转移方程可以采用式（5-70）描述，其中

式中，T=tk-1-tk为系统采样时间。

以上两种模型是目标运动模型中最基本的模型，也是目标跟踪中采用最多的模型，其计算量小，适合实时跟踪的需要。对于匀速、匀加速直线运动或者近似匀速、匀加速的运动，上述模型均能达到很高的跟踪精度。在实际应用中，也常用CA 模型来近似描述目标的机动。在目标机动性较弱的情况下，其机动可以看作是目标加速度的变化，将目标的加速度看作随机噪声，通过调整噪声的方差，可以近似目标的机动。但是，在目标的机动性较强的情况下，这样的模型对目标运动的描述显然是不精确的，需要采用与目标运动更为匹配的目标机动模型。

3.CT 模型

当目标做匀速转弯机动时，在笛卡尔坐标系内，每个时刻目标的速度和加速度都是变换的量，因此，相对CV 和CA 模型，CT 模型略微复杂。目标的状态采用矢量 sk=（xk，vxk，yk，vyk，wk）T描述，其中，（xk，yk）表示目标的位置，（vxk，vyk）表示目标的速度，wk 表示目标的转弯速率。对于被跟踪的目标，其状态转移方程依然可以采用（5-70）形式描述，其中

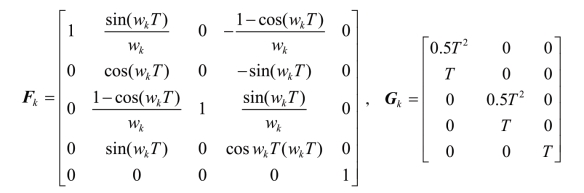
由此可见，在协同转弯CT 模型中，目标状态向量 sk中，wk 是作为角速率变量出现的，即 wk 通常是时变的。因此，在通常情况下，协同转弯CT 模型是非线性的模型，当采用该模型进行跟踪滤波时，需要采用诸如扩展卡尔曼滤波（Extended Kalman Filter，EKF）、无味滤波（Unscented Filter）等进行处理。当且仅当目标的转弯速率变量 wk 为常数时，协同转弯CT 模型可看成是线性模型。

4.Singer 模型

R.A.Singer 于20世纪70年代提出了Singer 模型，该模型假定机动模型为相关噪声模型，而不是通常假定的白噪声模型。设目标的加速度为 a（t），采用零均值指数相关随机过程描述，其相关函数为：

(www.xing528.com)

式中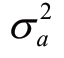，表示目标加速度方差。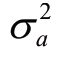的大小反映了目标的机动状况，可以利用目标的概率密度函数计算，一般假设机动目标的概率密度函数符合正态分布，假定目标机动的加速度范围为 [-amax，amax]，出现的概率为 Pmax，不出现的概率P0，则

描述目标的加速度为 a（t） 的随机过程可以利用线性时不变系统表示：

式中，w（t） 为零均值噪声；α 为机动时间常数的倒数，根据经验，对于逃避机动目标，α 取0.05 左右，转弯目标，α 取0.016 左右，对于大气扰动，α 取1。上式的离散形式表示为：

式中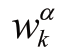，是方差为 σ2（1-β2）的零均值白噪声序列；β=e-αT。因此，Singer模型的连续状态空间方程表示为：

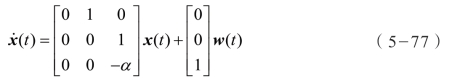
假定目标状态矢量X（k） 包含位置、速度和加速度，其离散状态方程表示为：

式中，状态转移矩阵 Φ（k）为：

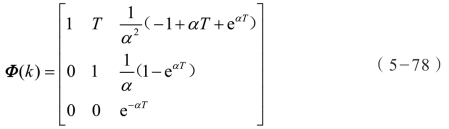
式中，噪声 w（k）的方差矩阵满足

式中

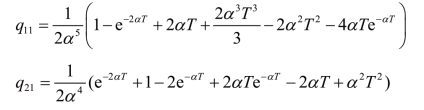
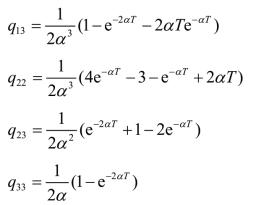
当αT ≪1 时，方差矩阵可以近似为

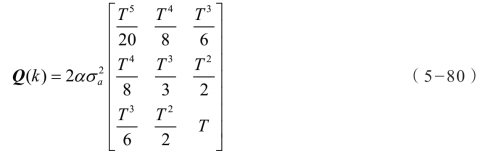
状态矩阵近似为：

此时Singer 模型近似为匀加速模型。当 Tα→∞时，Singer 模型将近似为匀速模型。可见，对于0＜Tα＜∞，Singer 模型相应地描述了介于匀速运动与匀加速运动之间的所有目标运动模式，与CV 和CA 模型相比，能够描述更加广泛的目标模型。