稳瞄控制系统模型及辨识方法优化方案

1.稳瞄系统伺服回路数学模型

稳瞄控制系统通常采用三闭环控制模式，图5-15给出了系统俯仰环的结构示意图。可以看出，主要部分为直流力矩伺服电动机和挠性陀螺，下面分别对两者理论模型进行分析。

图5-15　俯仰环伺服系统控制结构图

直流力矩电动机模型：为了提高系统的稳定精度，通常采用伺服直流力矩电动机，力矩电动机具有体积小、转动平稳、干扰力矩小等优点。在稳定平台中，直流力矩电动机的转子通过轴承与方位环和俯仰环的转轴固连在一起，在工作时，回路就是通过控制转子的转角来控制平台到达期望的位置的。直流力矩电动机的原理图如图5-16所示。

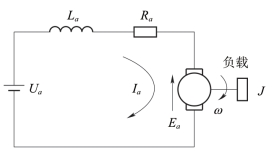
图5-16　直流伺服电动机的原理图

由图5-16可知，在电流连续的情况下，电枢回路的方程为：

式中，Ua 为控制电压；Ea 为电枢反电势；Ia 为电枢电流；Ra 为电枢回路总电阻；La 为电枢回路总电感。

电枢反电势公式为：

式中，Ce 为电动机的反电势系数；θ 为电动机转子转角。

力矩电动机的转矩公式为：

式中，Cm 为电动机力矩系数。

力矩平衡方程为：

式中，J 为稳定平台折算到电动机轴上的转动惯量；Md 为电动机的转矩；Mf为干扰力矩。

假设初始条件为零，对式（5-4）～式（5-7）进行拉普拉斯变换，得

根据式（5-8）可得力矩电动机的原理框图如图5-17所示。

图5-17　力矩电动机的原理框图

由图5-17可得Ua 和Mf 与的关系式为

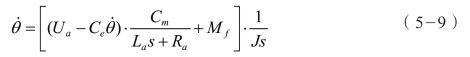
对式（5-9）进行变换，得

令电动机的机电时间常数，电气时间常数，则式（5-9）变为

在稳定平台中，由于平台折算到力矩电动机轴上的转动惯量J 比较大，使得机电时间常数Tm 在几百毫秒到几秒之间，电气时间常数Te 只有几毫秒，从而有 Tm＞＞Te，于是得到简化式（5-12）：

将式（5-12）代入式（5-11）中，得

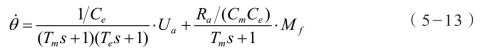
忽略Te 的影响，将传递函数进一步简化为一阶惯性环节，得

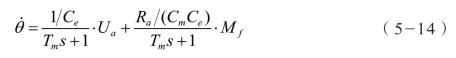
由式（5-14）可将图5-17简化为图5-18。

图5-18　力矩电动机的原理简化框图

表5-1给出了一组瞄准线稳定控制系统的力矩电动机参数，通过计算得到机电时间常数 Tm=0.28 s，电气时间常数 Te=0.002 s（可以忽略），代入图5-18中即可得到力矩电动机及平台负载的数学模型。

表5-1　力矩电动机及平台负载参数表

PWM 功率放大电路传递函数：近年来，随着电子器件的飞速发展，PWM 控制技术被广泛应用到对直流电动机的控制中，它利用微处理器的数字输出，经过模拟电路后，将模拟控制信号转换成相应的脉冲信号，从而达到控制电动机运动的目的。当PWM 输入控制电压改变时，其输出电压要到下一个周期才能改变，所以PWM 功放可以看成是一个滞后环节。用T 表示滞后时间，kpwm 表示PWM 的电压放大系数，则其传递函数为：

将上式中的e-Ts 按泰勒级数展开，由于一般情况下T 都很小，所以可以忽略高次项，则上式可以简化成一阶惯性环节：

在本系统中，PWM 放大电路的驱动频率远大于系统的截止频率，因此可以简化成一个比例环节：

瞄准线稳定回路：根据上述对各部件的分析，可得到瞄准线稳定回路的数学模型，如图5-19所示。

图5-19　瞄准线稳定回路的数学模型图

图5-19中，ωcmd 为给定角速度；Cm 为电动机力矩系数；Ce 为电动机的反电势系数；Ra 为电枢电阻；Tm 为机电时间常数；K 为陀螺的比例系数；ω为陀螺的固有频率；ξ 为陀螺阻尼系数；Mf 为干扰力矩；kpwm 为功放系数；为输出角速度；θf 为输出角度；ωb 为载体运动速度；G1（s）为位置环控制器；G2（s） 为速度环控制器。

将上节介绍的各个部分的数学模型代入图5-19中，可得系统俯仰环回路的固有环节传递函数为

由式（5-18）可以得到系统固有环节的波特图，如图5-20所示。从图中可以得知，系统的幅值裕度和相角裕度均大于零，系统是稳定的。当系统没有设计控制器时，其输出单位阶跃响应如图5-21所示。从图中可以看出，系统的超调量达到50%，调节时间大于2 s，远达不到瞄准线控制系统动态性能指标要求。因此，需要设计合适的控制器来提高系统的动态性能。

2.稳瞄系统模型辨识

准确的数学模型是进行控制系统设计的基本信息，模型的精确度直接影响了控制系统性能的好坏。为了更好地开展稳瞄伺服系统数字化设计，对控制回路控制器进行参数优化，需要对系统模型进行辨识。系统建模主要有两种方法，包括机理建模与辨识建模。机理建模依赖系统的物理特性，采用数学方法对系统进行原理分析，计算确定系统模型。如果系统内部结构复杂，各环节参数耦合性较强，采用机理建模所得到的模型往往与实际系统相比误差较大。因此，机理建模方法一般用于系统的定型分析，适用于条件受限、对模型精确度要求不高的系统。辨识建模则是通过实验获取不同输入信号对应输出信号之间的关系，利用一定的辨识算法估算出系统的模型。辨识建模只需要利用系统的输入、输出信息，适用于系统结构复杂或者对系统内部机理了解不多的情况。辨识建模主要分两类：参数模型辨识与非参数模型辨识。参数模型辨识是指假定一种模型结构，通过误差准则函数来确定模型参数，包括极大似然法、最小二乘法与梯度校正法等。非参数模型辨识不需要确定模型结构，主要是通过时域频域的响应曲线来描述系统的控制性能，包括阶跃响应法、脉冲响应法与相关函数法等。另外，近年来群优化智能算法发展与应用十分迅速，粒子群算法、神经网络算法、遗传算法等在系统辨识建模方面得到了广泛的运用。

图5-20　系统固有环节的波特图

图5-21　未加控制器时系统的阶跃响应

采用阶跃响应法进行模型辨识，通过采样获取的阶跃响应曲线计算伺服控制系统的传递函数。目前普遍采用的求取方法有近似法、半对数法、切线法、两点法和面积法等。通过分析发现，传统方法存在一定的缺陷，与群优化算法相结合是一种比较可行的办法。经过考虑，本项目采用改进遗传算法与阶跃响应法相结合的方法进行系统辨识。

（1）系统辨识的基本流程

系统辨识的程序主要分为以下几个步骤：根据辨识的目的，利用先验知识，初步确定模型的结构，采集数据并进行适当的处理；进行模型结构与参数辨识；最后通过验证得到最终的模型。系统辨识的基本过程如图5-22所示。

图5-22　系统辨识的基本过程

（2）基于改进遗传算法的系统辨识

目前，数字式火控系统的发展在我国仍属于研究阶段，准确建立稳瞄平台伺服系统电动机电枢模型对装甲车辆瞄准线数字控制系统的设计包括优化控制系统参数及设计控制系统的控制器意义重大。同时，因为系统内部结构复杂，存在难以用直接数学模型描述的线性环节，很难求得整个系统理想的机理模型。为此，对现有系统进行了大量的实验，采集输入/输出数据，结合稳瞄平台工作时电动机只在有限运行空间内进行正反转的实际情况，选择基于遗传算法与阶跃响应法相结合的辨识方法对某型装甲车辆瞄准线伺服电动机进行系统辨识。同时，考虑电动机直接辨识比较困难，采用将电流环看作一个整体进行辨识的方法，之后通过计算获得电动机电枢的数学模型。图5-23中虚线框内所示即为待辨识系统模型。(www.xing528.com)

实验方案通过电路电流限幅，选定输入阶跃信号的幅值，又因为稳瞄平台工作时受到空间位置限制，电动机只能在一定角度进行正反转，因为采用方波信号等效阶跃信号。采样周期设置为0.2 ms。之后通过三次样条插值预处理获取系统阶跃响应曲线，设计遗传算法，对确定的模型结构进行参数辨识，最后对结果进行验证，分析得出有效的模型。

图5-23　待辨识模型示意图

（3）遗传算法的改进

为了提高遗传算法运行的速度与效果，对遗传算法进行改进设计。包括：

变异概率自适应：对待辨识模型进行参数辨识时，取两个参数耦合编码为样本个体，使用二进制编码，选择操作采取保存最优个体的随机采样选取方法，交叉算子采用均匀交叉算子，变异算子采用随机变异算子，变异概率与变异位数随进化代数自适应调整。即

式中，t 为目前迭代次数；T 为总的迭代次数；N 为染色体位数；floor 函数为取整函数。

适应度函数设计：传统遗传算法进行系统辨识时，一般采用采样点误差平方和或其变形公式为适应度函数，编程运行足够代数之后，辨识参数获取效果如图5-24所示。由图进行阶跃响应性能指标误差分析，可知系统辨识效果比较差。分析原因是中间一些次重要采样点的误差干扰了关键参数点（比如峰值点等）的误差，因此，想要获得比较好的系统辨识结果，需要对适应度函数重新进行设计。突出关键点误差的调整作用，忽略次重要点误差，设计适应度函数。以阶跃响应性能指标超调量误差 emp、上升时间误差 etr、峰值时间误差 etp和调整时间误差 ets 加权为第i 次迭代的种群适应度函数，即

图5-24　采样误差适应度函数辨识效果图

其中，适应度函数系数 aij 由专家经验法与自适应调整方法结合确认。具体计算公式如下：

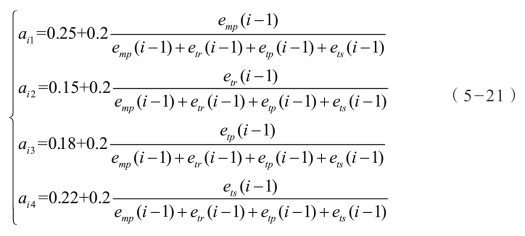
公式中 emp（i-1）、etr（i-1）、etp（i-1）、ets（i-1）分别为第i-1 次迭代最优个体超调量误差、上升时间误差、峰值时间误差和调整时间误差。取相同迭代次数与初始种群数量，式（5-21）为适应度函数，迭代结果如图5-25所示。可以看出，改进后的适应度函数对于加快收敛、增强系统辨识效果起到了很大的作用。

系统阶跃响应数据获取：为了能够获取控制对象相对准确的模型，首先利用控制系统与实验平台获取控制对象的阶跃响应输入/输出数据。为了保证稳瞄平台系统能够正常、稳定地运行，实验数据的获取是在系统电流闭环的情况下运行采集的。为了尽可能提高数据采样的精度，在充分考虑了控制系统的运行速度与反应时间后，选择了0.2 ms 为数据采样周期。同时，考虑到稳瞄平台系统平时工作的电流范围，采用单位阶跃响应曲线来反映系统性能，结合系统的稳定性能时间，采用幅值为0.5、周期为60 ms 的方波来等效阶跃信号作为输入。实验时，利用上位机程序控制DSP 系统实现输入/输出数据的采集。同时，利用DSP 系统处理数据的高速性，实现八点同时采样，而后取均值作为输出数据，以达到滤波的效果。获得的输入/输出数据曲线如图5-26所示。

图5-25　改变适应度函数辨识效果图

图5-26　输入/输出数据曲线

图中水平长短虚线为阶跃输入信号采样曲线，从零点开始。交叉点为输出数据采样点，实线折线为输出数据，即阶跃响应还原曲线。从图中可以看出，由于前期均值滤波，噪声的影响比较小，因此不需要再做滤波，但是可以看出阶跃响应曲线还原比较差，为了得到能够完整反映控制系统性能的阶跃曲线，需要对采样点做进一步的插值处理。

三次样条插值数据处理：目前，普遍使用的插值方法有线性插值、最临近插值、拉格朗日插值、Hemit 插值、牛顿插值、分段插值等。根据实际需要，采用三次样条插值，使插值获得的曲线连续且导数连续。三次样条插值是指曲线分段用三次多项式描述，并且在插值点连续且一阶、二阶导数连续。

即设y=f（x） 在点x0，x1，…，xn 的值为y0，y1，…，yn，若函数S（x） 满足以下条件：

则称S（x） 为函数f（x） 的三次样条插值函数，简称为三次样条。在Matlab 中编写M 文件，以Spline 函数实现三次样条插值，在区间范围内按照需求等间隔选取5 000 个插值点，获取插值图像，其中部分图像如图5-27所示。可以看出，三次样条插值相对于平滑曲线，还原效果十分明显，提高了超调量计算与调整时间、上升时间的计算准确度。

图5-27　三次样条插值处理效果对比

模型结构选择：在采集数据时，为了系统的稳定，采用电流闭环，但是实际想要辨识出的是电动机的传递函数，以便对电流环PI 控制器及后续控制加以设计，为此，把电流环剥离出来，把其他部分看作是被控对象。

图5-28所示为直流伺服电动机原理框图，可以看出输入电压与电枢输入电流的控制模型为一阶。加入PI 控制器参数与单位负反馈，电流闭环传递函数阶次为二阶，结合阶跃响应曲线形状，确定闭环传递函数阶次为无时滞二阶传递函数，具体形式为：

图5-28　直流伺服电动机原理图

因此，所要辨识确定的参数只有aw 与ξ 两个参数。实验中控制输入电压最大为10 V，实验时施加电压为1 V，对应的稳态值为1 V。为了便于指导控制器设计及计算，直接用电压采集值进行辨识计算。

模型参数辨识：在确定要辨识模型的阶次后，就可以根据系统的输入/输出数据，按照一定的辨识算法确定模型结构参数。采用遗传算法进行参数辨识。

设M 为种群的大小，Xi（i=1，2，…，M）为个体，重点对适应度函数进行比较设计后，选择超调量与调整时间、上升时间及峰值时间加权的方式作为适应度函数，具体算法步骤如下。

步骤1：置代数计数为t=0，通过随机数产生初始种群P0；

步骤2：提取染色体，还原参数值，通过适应度函数计算求得群体中每个个体的适应值，并进行排序；

步骤3：判断是否达到最大进化代数T，若是，则算法终止，否则，转步骤4；

步骤4：以概率Pv 进行选择操作，产生一些染色体，进入新一代种群P（t）；

步骤5：以概率Pc 进行交叉操作，产生一些染色体，进入新一代种群P（t）；

步骤6：以概率Pm 进行变异操作，产生一些染色体，进入新一代种群P（t）；

步骤7：t+1→t，转步骤2。

利用Matlab 软件，编写改进的遗传算法的程序，选取采样点误差、超调量误差、调整时间误差与上升时间误差加权的方法编写适应度函数，种群数量设为100，采用二进制编码，染色体长度为40，参数长度为20。迭代100 代后，其参数辨识结果为aw=0.000 903、ξ=0.359。系统辨识得到的模型传递函数为：

因此，系统辨识得到的开环传递函数为：

式中，R1=R2=2 kΩ，C1=0.01 μF，C2=0.033 μF。同时，电流环控制器如图5-29所示，以功放端电压为零，根据基尔霍夫定律，有以下公式：

图5-29　电流环控制器实现示意图

经过拉普拉斯变换迭代，获得电流环控制器传递函数表达式为：

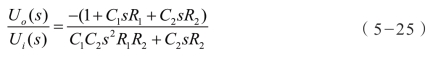
带入参数，得到电流环控制器数学模型为：

带入式（5-23），可以计算获得电动机控制模型为：

可以看出电动机模型近似为一阶系统，也满足低阶模型模拟高阶模型的原则，证明了系统辨识模型的正确性。

（4）辨识结果验证与分析

对于系统辨识，测量噪声和处理方法存在的误差，都可能导致辨识的误差，因此，需要对系统辨识结果进行量化效果评价验证。阶跃响应性能指标作为评价控制系统控制品质好坏的一种常用手段，通过仿真曲线与实际系统曲线的阶跃响应性能指标之间的误差或者相似度来评价辨识模型的好坏，通过不同辨识方法辨识模型的比较，评价辨识方法的好坏。在采用阶跃响应进行实验时，主要采用比较模型仿真输出与实际系统输出的上升时间、调整时间和超调量三个性能指标之间各自的偏差来评价。

选择递推最小二乘法作为对比辨识方法，使用Matlab 编写程序对同一组输入/输出数据进行辨识，辨识获得参数为aw=0.001、ξ=0.398 5，系统辨识得到的模型传递函数为：

按照辨识所得系统模型进行阶跃响应实验与阶跃仿真实验，所得结果如图5-30所示。可以直观地看到改进遗传算法系统辨识效果比最小二乘法系统辨识效果好。

图5-30　两种辨识方法辨识效果对比

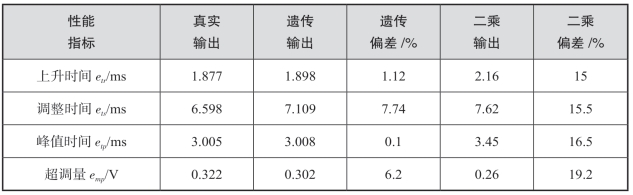
表5-2为根据阶跃响应指标定量分析两种辨识方法的结果。可以看出，遗传算法辨识方法输出和最小二乘法辨识输出的4 个性能指标相比，遗传算法辨识方法偏差更小，方法效果更好。证明了辨识方法的有效性与实验模型的有效性。

表5-2　两种辨识方法辨识效果定量分析