稳定控制系统误差分布与扰动特性分析

1.指向性能误差分布

设计瞄准线稳定系统时，首先要根据系统应用的性能需求确定稳定指向的性能指标，其标准通常是通过瞄准某个目标或使跟踪误差保持在一定范围内确定。对于随机扰动环境，指向误差的性能指标由指向误差保持在期望指标内的指向概率确定。性能指标确定后，分析所有误差源及每种误差对整个系统误差的贡献情况，各种误差分析为功能及性能设计提供了设计目标基础，所有电子、机械和伺服系统设计必须满足这些指标要求。

瞄准线稳定控制系统的误差主要包括传感器自身特征误差、传感器环境误差、目标/平台运动学特性产生的指向误差、传感器与稳定平台的失准误差等。系统的设计通常可以分成结构设计（机械）和刚体运动设计（控制和电子），采用有限元分析方法设计系统的结构，通过对刚体运动的仿真分析辅助指向和稳定伺服控制的设计。图5-12给出了稳定平台误差分布相关因素。瞄准线稳定控制系统的误差还可以分成短时影响误差，如运动引起的结构变形和刚体的动力学特性，以及长时偏差，如失准和漂移等。

详细的误差源分布状况需要深入部件级的特性，摩擦、振动产生的不平衡力矩导致的稳定扰动和平台的角速度、加速度都需要考虑；分析每个环节允许的残余误差；详细描述稳定平台的操作环境。此外，稳定控制的扰动从低频、中频到高频都存在，高频扰动通过结构设计和减震隔离消除。绝大多数隔离器都存在低频振荡现象，在共振频率附近很窄的区域内对扰动有放大作用，且一般与环境温度有关，在稳定控制中必须考虑这些影响。

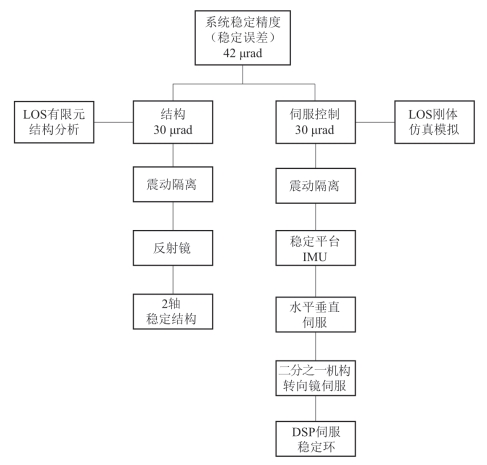
图5-12　稳定平台误差分布相关因素

基准偏差属于长时偏差，在系统完成特定功能的时间间隔内近乎为常数。抖动则是一种瞬时偏差。产生偏移误差的原因很多，跟踪过程中未对准、跟踪误差或滞后都可能产生，而平台的运动和震动又很难采用偏移误差和抖动误差来描述。对于不同的应用，其分布范围在1～10 Hz。图5-13给出了高低向位于水平向平台上的两轴稳定平台动态控制系统的误差分布情况，其中整体误差采用所有误差的均方根计算得到。均方根误差计算方法首先假定每个误差都是独立的，且符合正态分布。但实际情况通常很难符合这种假设，且经常存在非线性误差源。

将误差分为偏移（bias）和抖动（jitter）两类，根据系统结构和误差类型及稳定性能指标对误差进行量化。通常采用联合标准概率分布描述，假定指向误差是关于每个轴的正态分布，其分布可以采用偏移和抖动进行描述。偏移误差为平均偏差，而抖动误差为标准方差。对于每个轴上的任意偏移和抖动误差，联合分布非常复杂。如果假定关于每个轴的抖动误差都相等，偏移误差为每个轴偏移误差均方根，则可以将分布简化为Rician 分布，在这种情况下，指向概率可以描述为：

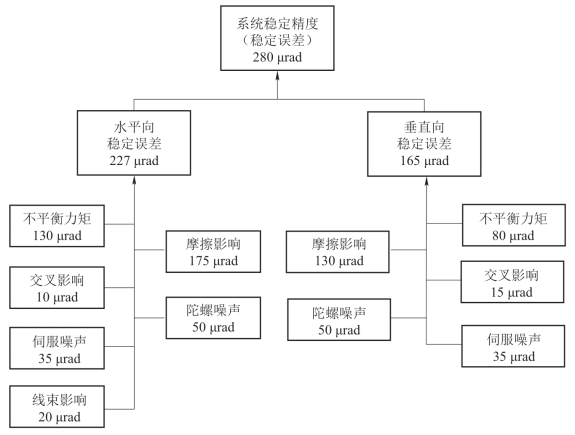
图5-13　某型高低向位于水平向框架内的稳定系统误差分配

式中，ΘB 为传感器视场或光束发散范围的一般；Θbias 为单轴基准偏差的均方根；σjitter 为单轴均方根抖动误差；I0（*）为零阶改进的贝塞尔函数。

积分边界和具体应用有关，可以是传感器视场角或光束波束的一半。可接受的偏差和抖动误差性能可以采用指向概率描述，当根据指向概率特性估计需要的性能时，非常有用。例如，图5-14给出的95% 指向概率的曲线，偏差和抖动误差归一化为允许的指向误差。

从图中可以看出，抖动误差小于1/3Emax 和移误差小于2/5Emax 归一化得到期望的指向概率。对于惯性指向应用，基准偏差必须包括IMU 和稳定平台上安装的陀螺的失准偏差及其他误差源。对于惯性指向系统，偏移误差包含IMU 与平台陀螺之间的失准误差及其他误差。在很多应用中，在评估性能时，目标能量比严格的指向概率更为有用。如激光通信系统，接收信号的能量特征更为重要。指向概率密度函数可以用来确定目标能量的平均估计，例如假定高斯密度强度为：

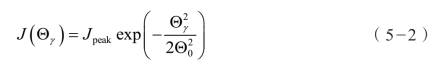
式中，Θ0 等于波束宽的1/4。目标接收到的平均能量为：

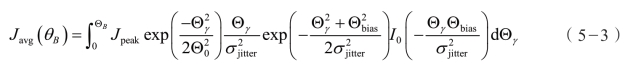
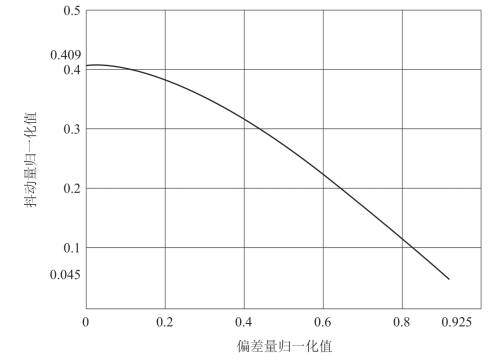
图5-14　Ppoint=0.95抖动和偏差归一化为Emax

2.稳瞄系统扰动特性

整个系统的误差分配到影响稳定系统性能的各个部分，包括传感器精度、传感器噪声、目标平台动力学产生的指向滞后、传感器与稳定平台的失准角及平台的残余运动等。同平台组件、稳瞄控制系统扰动及动力学特性等相关的误差主要包括：(www.xing528.com)

① 位置控制和跟踪误差。

② 传感器精度和噪声。

③ 气流引起的传感器噪声。

④ 偏移误差。

a.对准偏差：

i.传感器相对平台轴；

ii.平台轴相对基座。

b.轴间的正交误差。

c.伺服滞后。

⑤ 源自残余稳定的抖动。

a.不平衡。

b.平台的残余运动。

c.静态摩擦（密封组件、轴承、电动机等）。

d.动态摩擦。

e.反作用力矩。

f.交叉力矩。

g.陀螺噪声。

h.伺服/处理器噪声。

i.电动机纹波。

转矩与稳定误差的设计需要考虑的主要因素包括：转向加速度产生的不平衡力矩、动态和静态摩擦、电动机启动转矩、线缆和弹性约束。通常情况下，可以根据伺服控制环的动态响应特性设计简单的性能模型，用于完成转矩和稳定误差分析，并以确立的转矩和误差预算为基础，依据系统的性能需求确定各部组件的指标。

一旦选定了部组件，伺服设计模型可以转换为较为复杂的时域仿真模型，对平台的集合结构、部组件的非线性等进行仿真分析。通常这些模型可以用来验证系统的抗扰动能力，最终需要利用有限元分析方法分析稳定平台的机械结构设计需求。采用有限元分析方法可以预测结构响应特性，对伺服控制器设计而言，可以掌握伺服环响应带宽的限制。一旦有刚体仿真和有限元分析模型，然后验证系统的结构和算法性能需求，即可确定稳定控制结构或LOS 指向系统的实际性能。此外，如果需要震动隔离，与平台的连接方式也必须确定。跟踪或指向伺服环的设计只是上述过程的一部分，还未涉及跟踪算法的设计。跟踪算法的设计和性能测试通常作为一个独立的系统考虑。对于外环指向或跟踪环，平台相对目标的动力学是额外考虑的，与稳定控制环相比，通常带宽要求较低。