坦克炮控系统由高低向与水平向炮控系统组成,两者的系统结构基本相同,又可视为相互独立。下面以炮控的基本组成为基准,讨论炮控系统的数学模型。
(一)高低向炮控系统的数学模型
炮控系统高低向的系统结构框图如图4-15所示,它由陀螺仪、放大器、液压系统、火炮等部件组成。
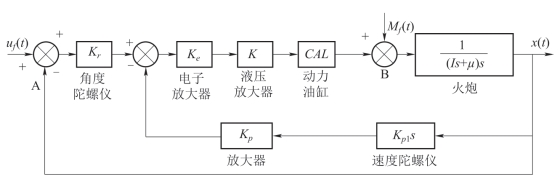
图4-15 炮控系统高低向系统框图
Kr、Ke、K、Kp、Kp1、CAL—各相应环节的放大系数;I—火炮转动惯量;μ—火炮转动黏性摩擦系数。
在充分考虑干扰力矩的情况下,输入和输出之间的关系为
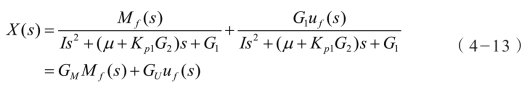
式中,G1=CALKKeKr;
G2=CALKKeKp;
GM=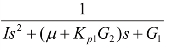 ;
;
GU=![]() 。
。
具体分析如下:
(1)陀螺仪
对于工程实际,角度陀螺仪作为敏感元件运用时,通常可看成一个放大环节,因此,高低向陀螺仪的输出为:
![]()
式中,Ucr 为角度陀螺仪的输出,为一个电压值;φa 为火炮高低方向的角度;x 为炮控系统的动态误差;Kr 为角度陀螺仪的放大倍数。
速度陀螺仪的输出为Ucp,并有
![]()
式中,Kp 为速度陀螺仪的放大倍数;Kp1 为比例系数。
因此,陀螺仪的综合输出为Uc,并有
![]()
(2)电子放大器
放大器通常由电阻网络、相敏放大、校正网络、直流放大及电源几部分构成。输入为电压信号,输出为控制电流。所以有:
![]()
式中,Ke 为放大倍数。
(3)液压放大器
液压放大器通常由两级液压放大环节组成,输出为动力油缸的上下腔压力差。基本传递函数为
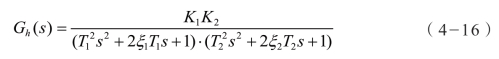
式中,K1、K2 分别为两级放大环节的放大倍数;T1、T2 分别为两级放大环节的时间常数;ξ1、ξ2 分别为两级放大环节的阻尼倍数。
液压放大器的时间常数T1、T2 的数值范围为0.005~0.01 s。火炮是一个大惯性元件,其时间常数大于0.5 s,所以液压放大器在工程上通常可以看成是一个放大环节,放大倍数为K=K1K2。
(4)动力油缸
动力油缸是炮控系统在高低向的执行部件,直接作用于控制对象——火炮,输出为稳定力矩Msta,典型数据模型是
![]()
式中,CAL 为动力油缸的放大倍数,其中,C 为比例系数,A 为油缸活塞的工作面积,L 为动力油缸耳轴与火炮耳轴之间的中心距;Δp 为上下腔的压力差。
(5)火炮
火炮为控制对象,具有惯量大的特点,绕火炮耳轴转动,动力学方程为
![]()
式中,Ja 为火炮转动惯量;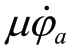 为炮控系统内部的转动黏性阻力矩;μ 为火炮转动黏性摩擦系数;Msta 为高低向稳定力矩;Mfa 为高低向耳轴摩擦力矩。(https://www.xing528.com)
为炮控系统内部的转动黏性阻力矩;μ 为火炮转动黏性摩擦系数;Msta 为高低向稳定力矩;Mfa 为高低向耳轴摩擦力矩。(https://www.xing528.com)
(二)水平向炮控系统的数学模型
炮控系统水平向的系统结构框图如图4-16所示,它通常由水平向陀螺仪、电子放大器、极化继电器、电动机扩大机、炮塔等部件组成。
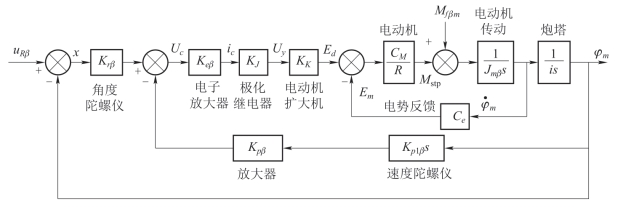
图4-16 炮控系统水平向系统框图
在上述框图中,uRβ 为水平向炮控系统的参考输入,Uy 为电动机扩大机激磁控制绕组的输入电压,Ed 为电动机扩大机输出的电动势,Em 为炮塔电动机输出的反电动势,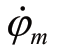 为电动机轴的角速度,Mstp 为水平向炮控系统的稳定力矩,也是电动机的电磁转矩,Mfβm 是炮塔座圈传递到电动机轴上的摩擦力矩,Jmβ 为电动机轴上的合成转动惯量,φm 为火炮在水平向的转角。
为电动机轴的角速度,Mstp 为水平向炮控系统的稳定力矩,也是电动机的电磁转矩,Mfβm 是炮塔座圈传递到电动机轴上的摩擦力矩,Jmβ 为电动机轴上的合成转动惯量,φm 为火炮在水平向的转角。
水平向陀螺仪和放大器的工作原理、模型与高低向的基本相同,不再重复介绍。
(1)极化继电器
极化继电器自身是一个开关式的非线性元件,但在系统里使用时,由于有反馈和加速线圈的作用,使极化继电器成为一个振荡化了的线性放大器,且不受电动机扩大机磁路饱和的影响而保持常数。
它的输入量为控制电流ic,输出量为电动机扩大机激磁绕组的控制电压Uy,放大倍数为KJ。
(2)电动机扩大机
一般都把电动机扩大机看成是两个惯性环节串联,但在炮控系统中看成振荡环节更为合适。另外,与电动机扩大机控制绕组相关的灭火花电路对扩大机时间常数有影响,因此可一并考虑,则扩大机的传递函数为:
![]()
式中,Tk 为电动机扩大机的时间常数,它的数值在10 ms 左右;ξk 为阻尼系数;Kk 为电动机扩大机的放大倍数。
由于电动机扩大机的时间常数很小,经常也将其看作是一个放大环节,放大倍数为Kk。
(3)炮塔电动机
炮塔电动机是水平向炮控系统的执行部件,输出为水平向的稳定力矩Mstp。由电力传动理论可知:
![]()
式中,CM 为电动机力矩系数(N·m/A);I 为炮塔电动机电枢回路的电流(A)。
又因为

所以
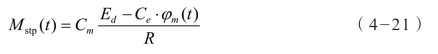
式中,Ce 为炮塔电动机反电动势的反馈系数(V·s/rad);R 为电动机扩大机和炮塔电动机回路的总电阻(Ω)。
(4)电动机传动与炮塔
电动机输出角速度为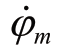 ,根据刚体转动的动力学方程,得
,根据刚体转动的动力学方程,得
![]()
式中,Jmβ 为电动机轴上的合成转动惯量,主要由炮塔电动机的转动惯量Jm、方向机折合到电动机轴上的转动惯量Jfm、炮塔折合到电动机轴上的转动惯量Jbam 三个部分构成。
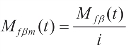 ,是折合到电动机轴上的外部干扰摩擦力矩,通常根据水平向的动力特性数据库选定。
,是折合到电动机轴上的外部干扰摩擦力矩,通常根据水平向的动力特性数据库选定。
动力学方程已经在电动机轴上建立,如式(4-18)所示,则可以发现,由电动机到炮塔的输出只是一个传动比为i 的减速过程,即
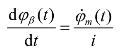
并由此可以得到电动机传动与炮塔的动力学方程为
![]()
综合上述各式,按照结构框图4-15可以得到水平向炮控系统的动力学方程为:

式中,G1β 为水平向炮控系统对动态角误差的放大倍数,表达式为:
![]()
G2β 为水平向炮控系统对火炮水平向角速度的阻尼系统,表达式为:
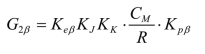
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




