外弹道问题模型的迭代-修正法：具有步长自动选择算法的弹道轨迹求解方法

当弹丸按一定方向和速度飞离炮口后，它会经历一个怎样的飞行过程？这是使火控系统命中目标要研究的重要问题之一，研究弹丸在这一过程的飞行规律就是外弹道问题。

（一）弹丸质点运动方程

弹丸在弹道空间的飞行过程是一个十分复杂的过程，它要受到多种因素的影响，为了便于研究，人们通常会对问题进行一定合理的假设，这里根据近程火炮射击的特点，做出如下与实际射击情况基本相符的假设：

① 假定飞行弹丸的章动角为零。章动角是指飞行弹丸的轴线与弹丸质心运动速度矢量之间的夹角。它一般只有几度，这一假定可将一个空气中的刚体运动简化为一个质点的运动。

② 弹道空间具有标准的气象条件。

③ 弹道空间的重力加速度g 为常数，且铅直向下。

④ 弹道空间的地表为平面，且忽略地球自转所产生的哥氏加速度。

在上述假定条件下，飞行中的弹丸可以用质心受力进行描述，如图2-5所示。其中，m 为弹丸质量，v 为速度矢量，F 为空气阻力。

由此可建立弹丸质心矢量运动方程为：

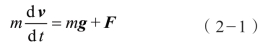
如果以火炮发射方向为x 轴正向，重力加速度负方向为y 轴正向，垂直于xOy 平面从左到右为z 轴正向，在非标准气象条件下，矢量方程（2-1）可以用如下微分方程组加以描述，这就是常见的外弹道微分方程组。

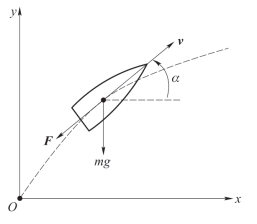
图2-5　弹丸质心运动受力

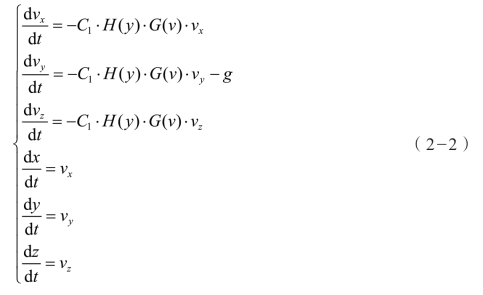
式中，vx，vy，vz 分别为弹丸初速在坐标系3 个投影轴上的分量；C1·H（y）·G（v）·vx 为x 方向的空气阻力加速度（其余依此类推）；

式中，ρ、ρ0 为实际条件和标准条件下的空气密度；

式中，i 为弹形系数；d 为弹芯直径；m 为弹丸质量；

式中，为标准阻力系数；a 为声速；为弹丸的马赫数。

图2-6即为标准的阻力系数曲线。曲线1 为西亚切定律阻力系数曲线（弹的长径比为1.2～1.5），曲线2 为1943年定律阻力系数曲线（长径比为3.0～3.5），它们分别代表两种标准弹的空气阻力系数。其他弹丸在选定标准阻力系数曲线后，只要求出弹形系数i，就可以知它的空气阻力系数。

图2-6　阻力系数曲线

1—西亚切定律阻力系数曲线；2—1943年定律阻力系数曲线。

方程组（2-2）的初始条件为：

t=0，x=0，y=0，z=0，vx0=v0cosα0，vy0=v0sinα0，vz0=0

式中，α0 为初始的瞄准角。

对于微分方程组（2-2），初始条件已知时的数值求解方法有多种，如欧拉矩形法、梯形法、龙格-库塔法等，其中四阶龙格-库塔法常用来精确数值求解微分方程。

所有这些方法都是在已知瞄准角α0 时，求取落点的方法。但在战车火控系统的弹道问题中，已知条件却是：

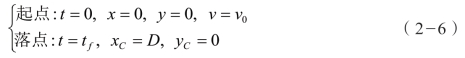
式中，D 为起落点之间距离，由激光测距机测得。

可见，这里的落点待求量D 为已知，而解算方程需要的初始条件瞄准角α0 却是火控系统需要获得的量，这是典型的两点边值问题。如何从边值条件（2-5）出发，求解火炮的瞄准角α0 和弹丸飞行时间tf，正是战车火控系统求解弹道问题的实质。

（二）弹道方程组边值问题的迭代-修正法

这里以弹道轨迹的某些物理特性为依据，提出如下具有步长自动选择算法的迭代-修正法，可将边值问题化为初值问题迭代求解。

（1）预先估计瞄准角

预估值可简单根据标准条件下距离D 和射角的关系得到。例如，可将表示为D 的二次函数，即

式中，ki 为根据弹道特性（有射表时可参考）选择的系数，i=0，1，2。

（2）按初值问题求解弹道微分方程组

有了瞄准角的估算值，即可求出精度不高的初始条件，因此对弹道微分方程组（2-2），可按初值问题选择步长h，用四阶龙格-库塔法进行数值求解。求解过程中，可形成各弹道诸元的序列值，即

其中，j 为整个迭代-修正法的迭代序号；i 为在积分计算过程中，以步长为h的递推计算序号。

当i=N+1 时，对于给定的某个大于零的误差允许值 1ξ，若有

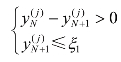
即认为此次初值问题的积分过程已经完成，并求得此次的距离计算值：

（3）根据落点诸元进行瞄准角修正

令Δx（j）=D（j）-D 为计算距离偏差，它可为正，也可为负。为正值时，应减小瞄准角；反之，则应增大。

这里以著名的弹道刚性原理为依据，求取修正瞄准角的计算式。

当 Δx（j）＞0 时，如图2-7（a）所示。假定在落点附近的一段弹道为直线，为落角的绝对值，则由距离偏差 Δx（j）在目标所在位置（即距离D处）产生的高度偏差 Δy（j）为：

图2-7　弹道落点偏差图

（a）Δx＞0；（b）Δx＜0

又因为

所以有

式中，、为落点C 处弹丸在x、y 方向上的速度分量，并且有

这就是说，以瞄准角射击时，在距离D 处产生了 Δy（j） 的高度偏差，按低伸弹道的刚性原理，此时瞄准角的修正量应该是：

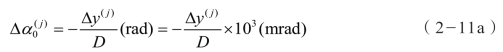
将 Δy（j）的算式代入，有：

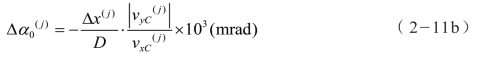
因此，α0 的修正公式是：

当 Δx（j）＜0 时，如图2-7（b）所示，此时在D 处有一个负方向的 Δy（j）偏差，不难证明，这时修正量仍按式（2-11）计算，并且它的数值为正。(www.xing528.com)

（4）步长h 的自动选择

每次迭代计算中，可根据落点提供的信息对积分步长h 进行选择，以保证计算的精确性。为了保证在落点C 处有（ξ2为落点处的水平允许误差），首先应满足的必要条件是。

为此，从到的步长h（即时间间隔）应按下式进行计算：

（5）迭代完成的条件

瞄准角及步长修正后，继续按龙格-库塔法返回到步骤（2）进行迭代计算。当进行第m 次迭代计算时，若同时满足：

则认为迭代计算完成，并取

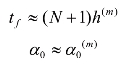
最后可求得火炮应装定的射角（通常在射表中将射角标记为 θ0）：

θ0=α0-γ

式中，γ 为跳角，也称为定起角，是火炮发射时由于多种原因产生身管跳动角度的平均值。

此外，现代战场上，战车火炮对低空目标的射击任务将会增加。如果已知目标的高度，以弹道高 yi 的函数作为迭代修正条件，也能完成类似的迭代-修正法的边值问题设计。

（三）外弹道方程的实时解算与参数修正计算

1.弹形系数或空气阻力的动态估计

弹道方程（2-2）是经过100 多年研究，已高度工程化、可进行数值计算的微分方程组。除了弹丸飞行的物理机理外，弹丸空气阻力的工程研究（如空气阻力系数曲线、弹丸的弹形系数等）是工程化的弹道微分方程的主要基础。然而，按传统的射表逼近算法，在射表未知甚至弹丸的弹形系数（或弹道系数）未知时，就将失去应用上述弹道方程的基础。因此，采用有效的算法实现弹形系数或空气阻力的估计，是射表未知时，研究弹道问题实时解算的关键所在。同时，如前所述，现代战车火炮的弹丸大多只追求中、近距离的穿甲能力，使得弹形系数（或弹道系数）在整个弹丸飞行过程中不能按常数处理。这就更需要寻求在不同射程上动态估计空气阻力或弹形（弹道）系数的实用算法。

在上述强约束条件下，解决这一理论问题的关键，是在数值求解弹道方程的龙格-库塔法中，逆向地应用空气阻力系数射击测定法的原理算法，只需已知弹丸在射程中的速度降，即可在弹道解算过程中同步实现弹形系数或空气阻力的逼近估计。同时，即使现代弹丸的弹形系数在全射程中为一变量，也能动态估计，从而在无射表的情况下，使弹道方程的实时解算成为可能。

这一弹形系数估计算法的理论推导如下：

在弹道微分方程（2-2）中，包含有弹形系数及阻力系数等参数的分别是弹道系数C1 和阻力函数G（vr）。为了便于综合，定义一弹道综合系数Ci，它的定义式为：

在i、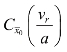等参数未知时，为了动态地求得Ci 的值，在数值求解弹道方程的龙格-库塔法中应用空气阻力系数射击测定法的算法。这一射击测定法的原理是，弹道低伸火炮的弹丸在飞行过程中动能的损失量等于弹丸克服空气阻力所做的功。当弹丸在某射程L 上的速度降已知时，即有：

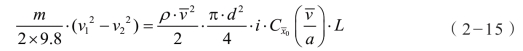
式中，L 为弹丸飞行的距离，在射击测定法中，多取L=1 000 m；v1、v2 为在射距L 上弹丸的初速和末速；v 为在射程L 上弹丸的平均速度。

上式整理得：

代入式（2-8）得：

式（2-17）即为在龙格-库塔法的积分过程中，迭代估计弹形系数的数学公式。式中，L、v1、v2 等既是射程射击实验中的已知参量，也可以在龙格-库塔法的积分过程中求得，后者向前者的逼近，可为弹形系数估计的迭代算法提供修正条件。

对于战车中装备的非低伸弹道的弹种，如破甲弹、榴弹等，也可以近似利用这一算法求得弹道综合系数Ci，此时能量转换公式应修正为：

式中，k 为大于1 的修正系数。

可见，只要知道射程L 上的速降Δv=v1-v2，L 范围内的弹道综合系数就为已知，并且在龙格-库塔法的解算过程中，对L 进行平移。根据弹丸的实际速降特性，即使弹形系数i 在全弹道过程中为一变量，也可动态地确定Ci 的值。当然，这一算法的启动仍然需要知道一定的初始条件，主要是一定射程（L）上的弹丸速降。取得这样的数据并不难，只要进行某一小射角的射程射击实验就可以了。这与只有已知射表，才可以进行弹道逼近方程的解算情况相比，已有质的改观。例如，在标准气象条件下，根据某坦克炮穿甲弹的射程射击实验数据，求得：Ci=8.319 6×106。同理，其榴弹为Ci=2.969 6×106。

由于弹道综合系数Ci 的引入，方程（2-2）所示的弹道微分方程组将变为：

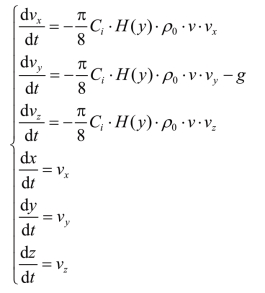
实际射击条件与标准射击条件下，由弹道参数偏差所引起的射击诸元差值的计算，称作修正量计算。现行以射表为基础的弹道逼近算法中，由于实际射击条件与标准射击条件存在差异，修正量计算是一项必不可少而又十分烦琐的弹道计算任务。必须要指出的是，弹道方程各个修正量之间是相关的，但现行的修正量计算并没有按修正计算本身的物理机理，将各种偏差引入弹道方程中予以综合计算，只是对各个偏差分离地进行修正，忽略了它们之间在非线性弹道微分方程中必然存在的耦合效应，既烦琐，精度也难以提高。如何解决这一技术问题，也是火控弹道问题所面临的重要任务之一。

2.对Ci、H（y）等弹道参数偏差的修正计算

非标准条件下的气温、气压对弹道方程的影响主要体现在实际的空气密度ρ 上，它将通过弹道参数Ci 与空气密度函数H（y）对弹道方程产生影响。大气中的气体为多种单质气体的混合气体，根据大气热力学原理，气体的宏观状态可以用压强、温度和密度等变量来描述。在温度不太低、压强不太高的条件下，气体的状态方程为：

式中，ρ 为空气密度（kg/m3）；p 为大气的压强（Pa）；T 为大气的绝对温度（K）；R 为特定气体的气体常数。

根据阿伏伽德罗定律，可以求得适合各种气体的气体常数。

对于1 mol 的任意气体，有：

式中，μ 为气体的相对分子质量。

mol（摩尔）为气体粒子数量的单位，1 mol 是指分子数量为NA=6.02×1023 个单质气体的总称（NA 为阿伏伽德罗常数）。

上式说明，气体的相对分子质量μ 越大，则R 越小。空气是一种主要由氮气和氧气所组成的混合气体。根据空气的组成成分计算得到的平均相对分子质量为μ=28.97，因此，空气的气体常数为R=287 J/（kg·K）。

方程（2-19）为理想大气的状态方程，但是实际射击条件下的空气并非理想大气，在通常情况下，空气中含有水汽，称为湿空气。湿空气的状态方程为

式中，Tv 为虚温。

虚温Tv 的表达式为

式中，pe 为水汽的分压（Pa）。

用式（2-21）的实际空气密度ρ 对Ci、H（y）等弹道参数进行修正后，在弹道方程（2-2）的解算过程中，可自然完成气象条件偏差所引起的修正量的综合计算。

3.对初速v0 偏差的修正计算

在非标准弹道条件下，药温、炮膛磨损都会造成弹丸初速的变化。但是，这些变化规律属于内弹道学的范畴，受制于内弹道学的规律，目前，初速的修正仍要以经验公式为主。

对某型火炮，药温偏差与初速偏差的关系式为：

式中，Δv0 为由药温偏差引起的初速v0 的偏差量（m/s）；

Δt=t-15，为药温t 对标准温度（15 ℃）的偏差（℃）；

式中，v045 为+45 ℃时的实测初速值；v015 为+15 ℃时的实测初速值。

炮膛磨损与初速偏差的关系式为：

式中，Δv0w 为由炮膛磨损引起的初速v0 的偏差量（m/s）；Δw 为药室长度的增加量（m）；f（Δw）为药室增长量的函数，可由实际测量确定。

此外，弹重和装药量等因素也会对v0 产生影响，它们的关系式与式（2-25）相似。

因此，解算弹道方程的重要初始条件，弹丸的实际初速vs0 为：

将vs0 代入弹道方程中，通过弹道方程的解算，即可实现初速偏差的修正量的综合计算。