理想的距离保护时限特性，应该是动作时间与故障点到保护安装处的距离成正比，即故障点离保护安装处越近，动作时间越短；故障点离保护安装处越远，动作时间越长。实际上要实现上述时限特性太困难，所以，到目前为止，距离保护仍为阶段式特性。距离保护的整定计算就是根据被保护电力系统的实际情况，确定距离保护Ⅰ段、Ⅱ段和Ⅲ段测量元件对应的整定阻抗以及Ⅱ段和Ⅲ段的动作时限。
当距离保护应用于双侧电源的电力系统时，为便于配合，一般要求保护Ⅰ段和Ⅱ段的测量元件具有明确的方向性，即采用具有方向性的测量元件。Ⅲ段为后备段，包括对本线路Ⅰ、Ⅱ段保护的近后备，相邻下一线路保护的远后备和反向母线保护的后备，所以Ⅲ段通常采用有偏移特性的测量元件。如图3−2−1所示，以各段测量元件均采用圆形动作特性为例，绘出了它们的动作区域，为使各测量元件的整定阻抗方向与线路阻抗方向一致，复平面坐标的方向作了旋转，圆周1、2、3 分别为线路AB 的A 处保护Ⅰ、Ⅱ、Ⅲ段的动作特性圆，4 为线路BC 的B 处保护Ⅰ段的动作特性圆。
图3−2−1 距离保护各段动作区域示意
下面讨论各段保护具体的整定原则。
距离保护各段配合（视频）
1.距离保护Ⅰ段的整定
距离保护Ⅰ段为瞬时动作的速动段（动作时限为零，不含阻抗元件的固有动作时间），同电流保护Ⅰ段一样，它只反映本线路的故障，为保证动作的选择性，在本线路末端或下级线路始端故障时，应可靠地不动作。其测量元件的整定阻抗，按躲过本线路末端短路时的测量阻抗来整定，即
式中 
——距离保护Ⅰ段的整定阻抗；
Z AB ——本线路末端短路时的测量阻抗；
Z1 ——线路单位长度的正序阻抗；
lAB——被保护线路的长度；
K rel ——可靠系数，由于距离保护为欠量动作，所以K rel ＜ 1，考虑到继电器动作阻抗及互感器误差等因素（在线路较短时，还应当靠考虑绝对误差），一般取K rel =0.8 ～0.85。
式（3−2−1）表明，距离保护Ⅰ段的整定阻抗值为线路阻抗值的0.8～0.85 倍，整定阻抗的阻抗角与线路阻抗的阻抗角相同。这样，在线路发生金属性短路时，若不考虑测量误差，则其最大保护范围为线路全长的80%～85%，否则不能满足选择性的要求。
2.距离保护Ⅱ段的整定
为了弥补距离保护Ⅰ段不能保护本线路全长的缺陷，增设距离保护Ⅱ段，要求它能够保护本线路的全长，保护范围需与下级线路的距离保护Ⅰ段（或距离保护Ⅱ段）配合。
如图3−2−2所示，电网结构复杂，还有其他回路的影响，因此，距离保护需要考虑分支电路的影响。
1）分支电路对测量阻抗的影响
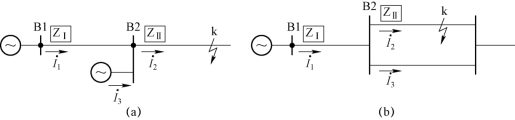
图3−2−2 分支电路对测量阻抗的影响
（a）助增分支；（b）外汲分支
图3−2−2 中k 点发生短路时，B1 保护处的测量阻抗为
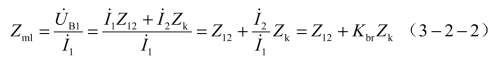
式中 Z12——母线B1、B2 之间线路的正序阻抗；
Zk——母线B2 与短路点之间线路的正序阻抗；
Kbr——分支系数。
在图3−2−2（a）所示的情况下，
其值大 于1，使B1 处保护测量到的阻抗Zml 大于阻抗Z12+Zk。这种使测量阻抗变大的分支称为助增分支，对应的电流 3I称为助增电流。
在图3−2−2（b）所示的情况下，
其值小 于1，使保护l 测量得到的阻抗Zml 小于阻抗Z12+Zk。这种使测量阻抗变小的分支称为外汲分支，对应的电流 3I称为外汲电流。
助增分支电路对距离保护的影响（动画）
外汲分支电路对距离保护的影响（动画）
2）距离保护Ⅱ段的整定阻抗
距离保护Ⅱ段的整定阻抗应按以下两个原则进行计算：
（1）与相邻线路距离保护Ⅰ段配合。为了保证在线路2 上发生故障时，保护1 的Ⅱ段不越级跳闸，其Ⅱ段的动作范围不应该超出保护2 的Ⅰ段的动作范围。若保护2 的Ⅰ段的整定阻抗为
则保护1 的Ⅱ段的整定阻抗应为
式中 Kr′el，Kr′el——可靠系数，一般取Kr′el =0.8 ～0.85，Kr′el =0.8。
当电网的结构或运行方式变化时，分支系数Kbr 会随之变化。为确保在各种运行方式下保护1 的Ⅱ段范围不超过保护2 的Ⅰ段范围，式（3−2−3）的Kbr.min 应取各种情况下的最小值。
（2）与相邻变压器的快速保护配合。当被保护线路的末端接有变压器时，距离保护Ⅱ段应与变压器的快速保护（一般是差动保护）配合，其动作范围不应超出相邻变压器快速保护的范围，整定值按躲过变压器低压侧出口处短路时的阻抗值来确定。设变压器的阻抗为Zt，则距离保护Ⅱ段的整定值应为
式中 Kr′el，K r′el——可靠系数，一般取Kr′el =0.8 ～0.85，K r′el =0.7 ～0.75。
当被保护线路末端变电所既有出线，又有变压器时，线路首端距离保护Ⅱ段的整定阻抗应分别按式（3−2−3）和式（3−2−4）计算，与所有的相邻出线的Ⅰ段配合，并取最小者作为整定阻抗。
如果相邻线路的Ⅰ段为电流保护或变压器以电流速断为快速保护，则应将电流保护的动作范围换算成阻抗，然后用上述公式进行计算。
3）灵敏度校验
距离保护Ⅱ段应能保护线路的全长和下级线路首端的一部分，本线路末端短路时，应有足够的灵敏度，其可以用保护范围来衡量。考虑各种误差因素后，要求灵敏系数应满足
如果Ksen 不满足要求，则距离保护Ⅱ段应改为与相邻元件的Ⅱ段保护配合。
4）动作时间的整定
距离保护Ⅱ段的动作时间与下级线路Ⅰ段配合，在与之配合的相邻元件保护动作时间的基础上，高出一个时间级差Δt，即
式中 
——与本保护配合的相邻元件保护段（x 为Ⅰ或Ⅱ）的动作时间。
时间级差Δt 的选取方法与阶段式电流保护中时间级差的选取方法相同。
3.距离保护Ⅲ段的整定
1）距离保护Ⅲ段的整定阻抗
距离保护Ⅲ段为后备保护，应保证在正常运行时不动作。其整定阻抗按以下几个原则计算：
（1）按与相邻下级线路距离保护Ⅱ或Ⅲ段配合整定。
首先考虑与相邻下级线路距离保护Ⅱ段配合，即
可靠系数的取法与距离保护Ⅱ段整定类似。
如果与相邻线路距离保护Ⅱ段配合灵敏系数不满足要求（一般较难满足），则应改为与相邻线路距离保护Ⅲ段配合，即
（2）按与相邻下级变压器的电流、电压保护配合整定，则整定计算为
式中 Zmin——电流、电压保护的最小保护范围对应的阻抗值。
（3）按躲过正常运行时的最小负荷阻抗整定。当线路上负荷最大时，即线路中的电流为最大负荷电流且母线电压最低时，负荷阻抗最小，其值为
式中 
——负荷情况下母线电压的最低值；
——母线额定电压。
IL.max ——最大负荷电流；
参考过电流保护的整定原则，考虑到外部故障被切除后，电动机自起动的情况下，距离保护Ⅲ段必须立即可靠返回的要求，即故障切除后，应当可靠返回。
若采用全阻抗特性，动作阻抗即整定阻抗，整定值为
式中 Krel——可靠系数，一般取Krel=0.8～0.85；
Kast——电动机自起动系数，取Kast=1.5～2.5；
Kre——阻抗测量元件的返回系数，取Kre=1.15～1.25。 若采用方向特性，则负荷阻抗与整定阻抗的阻抗角不同，动作阻抗随阻抗角的变化而变化，只有当阻抗角等于最大灵敏角时，动作阻抗才等于整定阻抗。整定阻抗为
(www.xing528.com)
式中 φset——整定阻抗的阻抗角；
φL——负荷阻抗的阻抗角。
按上述3 个原则进行计算，取其中的最小者作为距离保护Ⅲ段的整定阻抗。
当距离保护Ⅲ段采用偏移特性时，反向动作区的大小通常用偏移率来整定，一般情况下偏移率取为5%左右。
2）灵敏度校验
距离保护Ⅲ段一方面作为本线路Ⅰ、Ⅱ段的近后备保护，另一方面作为相邻设备的远后备保护，灵敏度应分别进行校验。
作为近后备保护时，按本线路末端短路校验，即
作为远后备保护时，按相邻设备末端短路校验（如果有几个相邻线路，考虑几个远后备保护时，应取这几个灵敏度中的最小值），即
式中 Znext——相邻设备（线路、变压器等）的阻抗；
Kbr.max——相邻设备末端短路时分支系数的最大值。
相邻线路灵敏度需考虑分支系数的影响，取其中最大的分支系数。
3）动作时间的整定
距离保护Ⅲ段应按照阶梯原则确定动作时限，且需大于最大的振荡周期（1.5～2 s）。
距离保护的时限特性（动画）
4.将整定参数换算到二次侧
在上面的计算中，得到的都是一次侧的参数值，实际应用时，应把这些值换算至二次侧。设电压互感器TV 的变比为nTV，电流互感器TA 的变比为nTA，系统的一次参数用下标“（1）”标注，二次参数用下标“（2）”标注，则一、二次测量阻抗之间的关系为
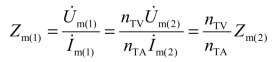
即
整定阻抗也可以按照类似的方法换算到二次侧，即
5.整定计算举例
在图3−2−3所示的110 kV 网络中，各线路均装有距离保护装置，已知ZsA.max=20 Ω，ZsA.min=15 Ω，ZsB.max=25 Ω，ZsB.min=20 Ω，线路AB 的最大负荷电流IL.max=600 A，功率因数cosφL=0.85，各线路每千米阻抗Z1=0.4 Ω/km，线路阻抗角φk=70°，电动机的自起动系数Kast=1.5，保护5 Ⅲ段动作时间
=2s，正常时母线最低工作电压UL.min 等于0.9UN（UN=110 kV）。试对其中保护1 的相间短路保护Ⅰ、Ⅱ、Ⅲ段进行整定计算
各段均采用相间接线的方向阻抗继电器）。
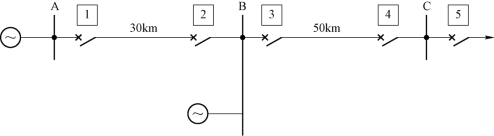
图3−2−3 网络连接图
解 （1）有关各元件阻抗值的计算。
线路12 的正序阻抗：Z12=Z1L12=0.4×30=12（Ω）；
线路34 的正序阻抗：Z34=Z1L34=0.4×50=20（Ω）。
（2）距离保护Ⅰ段。
① 整定阻抗：按式（3−2−1）计算，则有
② 动作时间：t(Ⅰ )=0 s（指不再人为地增设延时，Ⅰ段实际动作时间为保护装置固有的动作时间）。
（3）距离保护Ⅱ段。
① 整定阻抗：
与相邻线路34 的保护3Ⅰ段配合，按式（3−2−3）整定，即
取
的计算如下：Kbr.min 为保护3 的Ⅰ段末端发生短路时对保护1 而言的最小分支系数，如图3−2−4所示，当保护3 的Ⅰ段末端k 点短路时，分支系数计算式为
图3−2−4 整定距离保护Ⅱ段时求Kbr.min的等值电路
可以看出，为了得出最小的分支系数Kbr.min，ZsA 应取最小可能值，即应取电源A 的最大运行方式下的等值阻抗ZsA.min，而ZsB 应取最大可能值，即取电源B 最小运行方式下的最大等值阻抗ZsB.max，因而
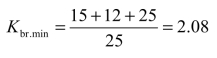
于是
② 灵敏度校验：按本线路末端短路求灵敏系数
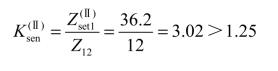
满足要求。
③ 动作时间，与相邻保护3Ⅰ段配合，则
它能满足与相邻保护配合的要求。
（4）距离保护Ⅲ段。
① 整定阻抗：按躲开最小负荷阻抗整定。因为继电器取为相间接线方式的方向阻抗继电器，所以按式（3−2−11）计算
且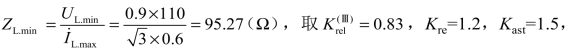
φset=70°，φL=arccos(0.85)=32°，于是
② 灵敏度校验。
a.本线路末端短路时的灵敏系数为
满足要求。
b.相邻元件末端短路时的灵敏系数按式（3−2−14）计算，即
式中 Kbr.max——相邻线路34 末端k 点短路时对保护1 而言的最大分支系数，求该系数的等值电路如图3−2−5所示。
图3−2−5 距离保护Ⅲ段灵敏度校验时求Kbr.max的等值电路
取 ZsA 的最大可能值为 ZsA.max，ZsB 的最小可能值为 ZsB.min，于是
不满足要求，可增大整定阻抗，同时增加阻抗限制措施。
③ 动作时间为
6.对距离保护的评价
根据上述分析和实际运行的经验，对距离保护可以作出如下评价：
（1）阻抗继电器是同时反映电压的降低与电流的增大而动作的，因此距离保护比单一反映电流的保护的灵敏度高。距离保护Ⅰ段的保护范围不受电网运行方式变化的影响，保护范围比较稳定，Ⅱ、Ⅲ段的保护范围受运行方式变化的影响（分支系数变化），能满足多电源复杂电网对保护动作选择性的要求。
（2）距离保护Ⅰ段的整定范围为线路全长的80%～85%，对双侧电源网络，至少有30%的范围保护要以Ⅱ段时间切除故障。在双端供电系统中，有30%～40%区域内故障时，两侧保护相继动作切除故障，若不满足速动性的要求，则必须配备能够实现全线速动的保护——纵联保护。
（3）距离保护的阻抗测量原理，除可以应用于输电线路的保护，还可以应用于发电机、变压器保护，作为其后备保护。
（4）与电流、电压保护相比，由于阻抗继电器本身构成复杂，距离保护的直流回路多，振荡闭锁、断线闭锁等使接线、逻辑都比较复杂，调试比较困难，装置自身的可靠性稍差。
距离保护的应用：在35～110 kV 电网作为相间短路的主保护和后备保护，采用带零序电流补偿的接线方式，在110 kV 电网中也可作为接地短路故障的保护。在220 kV 电网中作为后备保护。另外，接地阻抗继电器还可作重合闸装置中的选相元件，与高频收发信机配合，可构成高频闭锁（或允许）式距离保护。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
