电池储能系统的物理模型分析

为了控制电池储能系统有效提升目前电力系统的运行质量，进一步研究和建立电池储能系统的通用数学模型是建立先进电池储能系统的重要技术基础。本节将针对电池储能系统的不同运行环境，对多种电池储能系统的数学模型进行详细的介绍和分析，并讨论不同种类数学模型的不同适用环境和具体应用。

电池储能调频系统主要包括电池本体、功率变换系统以及调频服务控制器等主要子系统。其中电池本体负责电能的存储与释放；功率变换系统负责在电池的直流输出与交流电网间完成功率的双向传输变换；调频服务控制器负责生成电池储能系统的具体调频服务控制运行信号。典型的电池储能系统的各个部分可由图5-4描述，具体包括储能单元本体，DC/DC电压变换模块以及DC/AC变流器模块。对于多组串联的高压电池结构也可省略DC/DC电压变化模块电池储能单元本体直接通过DC/AC变流器模块与电网相连。

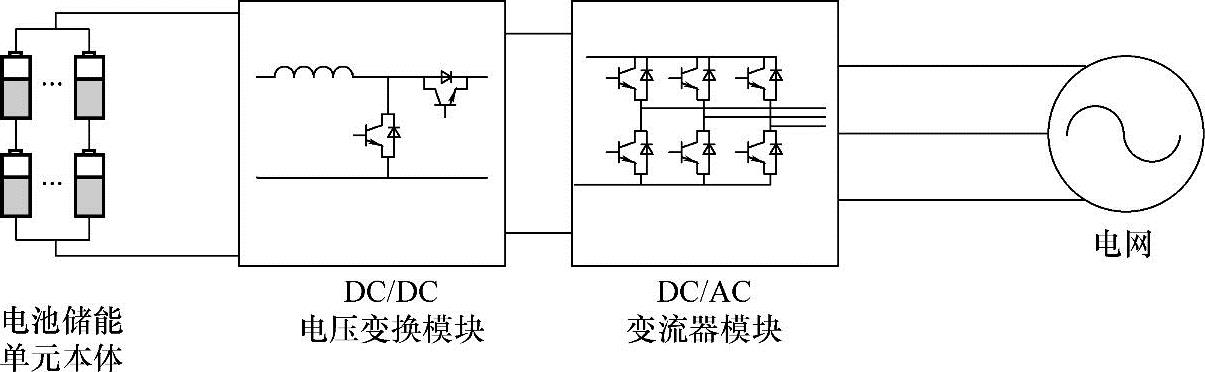
图5-4　典型电池储能系统构成架构

1.电池储能理想模型

电池储能系统的理想能量容量模型可由式（5-7）确定的一个一阶系统进行描述，即

SOC_i+1=SOC_i-P_i^Bat （5-7）

式中 SOC_i和SOC_i+1——分别为电池储能系统在i和i+1时刻的系统可用容量，

以百分数形式进行表示；

P_i^Bat——电池储能系统在i时刻的输出功率，以放电功率为正方

向。电池储能系统的可用能量容量仅由输出功率影响，

并且不考虑充放电过程中产生的能量损耗。

2.考虑充电功率损耗的储能容量计算模型

当考虑充放电过程中的能量损耗时，原有的电池储能系统能量容量模型可以由式（5-8）进行描述：

SOC_i+1=SOC_i+η_ChP^Bdt_Dis,i-P^Bat_Dis，i/η_Dis （5-8）

式中 η_Ch和η_Dis——分别表示电池本体充电和放电过程中的运行效率，取值范围

介于0至100%之间。

与上面的电池储能系统理想模型相比，电池本体的充放电功率被分离充电功率和放电功率，分别由P^Bat_Ch，i和P^Bat_Dis，i表示，均为非负变量。这样电池的能量容量模型可以进一步考虑充放电过程中功率损耗对电池可用能量容量估算的影响。与此同时，通过进一步细化充电功率的运行方向，可以分别对充电和放电过程中的功率损耗进行计算和考虑。充电过程中的功率损耗会导致电池本体得到的充电功率小于全系统与电网间传送的充电功率，因此在计算电池储能系统的可用能量变化时需要将充电功率乘以相对应的充电效率用于计算电池储能系统在下一控制时刻的可用能量容量。反之，对于放电过程，从电池储能元件本体释放出的电能在考虑各个部件运行损耗的情况下应大于最终输送到电网中的实际能量。因此在计算电池储能系统可用容量时，需要将注入电网中的放电功率除以对应的放电效率。

3.电池储能元件动态模型

大部分种类的电池本体元件在充放电过程中都会存在着一定的动态特性，即电池本体的可用能量在结束充放电过程后会随时间的推移出现一定的变化。尤其是在大功率运行的情况下这种效应更为明显。考虑到当前电池储能系统的建造成本仍然较高，因此充分利用电池储能系统的可用能量容量将有效提升电池储能系统的经济性。为此，下面将主要介绍考虑电池储能元件本体的运行动态特性，以便在电池储能系统运行过程中更加准确地对电池储能系统的可用能量容量进行评估计算。

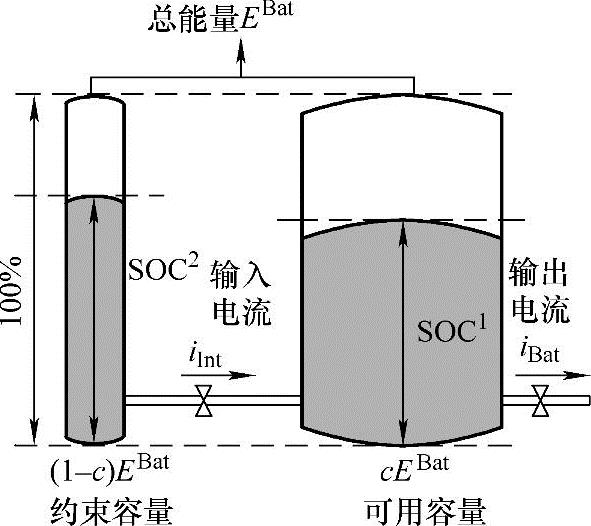
图5-5　电池储能系统动态等效模型

为了考虑电池储能系统可用能量容量的运行动态特性，有学者提出可以将理想模型中的电池系统能量容量分为两部分进行建模。这两部分可用容量可以使用图5-5描述的容器系统进行类比说明。(www.xing528.com)

图5-5中将电池储能系统的能量容量表示为两个相互独立的容器。每个容器中储存的液体代表了各自存储的可用容量，而各容器的液体水位表征了电池储能系统的SOC。其中右侧的容器存在着两个管道分别与外界和左侧的容器相连接。与外界相连接的管道代表了储能系统与电网间的能量交换，与左侧容器的管道代表了储能系统内部的能量交换，用于对储能系统的能量动态过程进行建模。左侧的容器仅通过管道与右侧的容器交换能量，无法直接与外界产生直接联系。两个容器间的能量交换功率大小由两个容器间的能量水平之差决定，即

P_i^Int=k^ic（SOC²_i-SOC¹_i） （5-9）

式中 P_i^Int——电池储能系统两部分可用容量间的交换功率；

SOC_i¹和SOC²_i——分别表示两部分能量容量中各自的剩余可用能量水平；

k^ic——交换功率与可用能量水平差值之间的线性系数。

进一步地，各个容器中所代表的可用能量水平（SOC）可由式（5-10）、式

（5-11）进行计算评估：

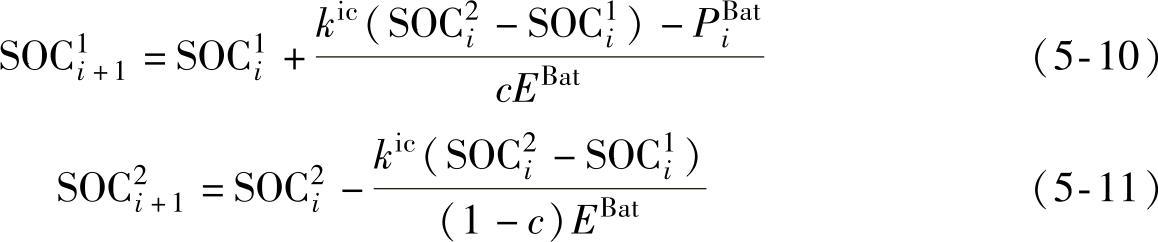
式中 E^Bat——电池储能系统的整体容量容量；

c——右侧可与外界直接交换能量部分的能量容量，取值范围为0～1之间。

进一步地，将可用能量容量分为两部分表示的电池储能系统动态模型可以由式（5-12）系统状态方程进行描述：

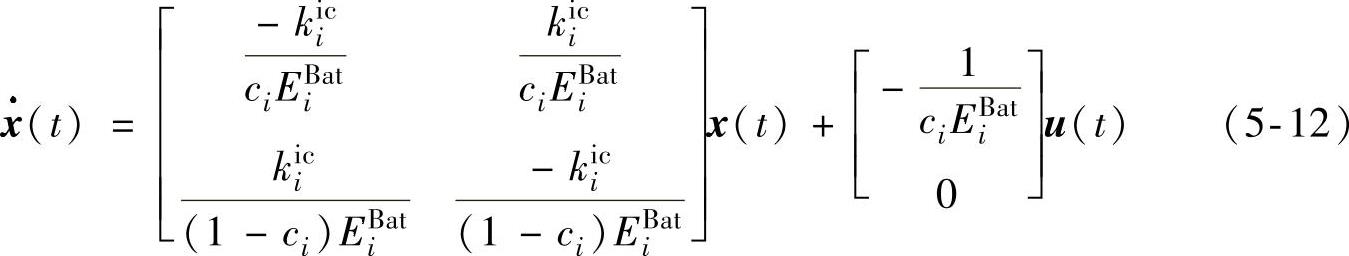
式中，x（t）=[SOC¹（t）SOC²（t）]，u（t）=P^Bat。

由此，考虑电池储能系统的能量容量动态效应的系统动态模型可由上式进行描述。上述电池储能系统的动态模型可以进一步与先进优化控制器相结合，用以量化计算电池储能系统在未来指定时刻的可用剩余能量（SOC）水平，以便实现最大化电池储能系统技术效用的目标。

4.电池储能能量变换系统模型

考虑到目前DC/AC变流器可以通过解耦控制，实现电池储能系统的输出有功功率和无功功率解耦控制。因此由DC/DC和DC/AC部件构成的功率变换系统（Power Conversion System，PCS）系统数学模型可由一个1阶惯性系统进行数学建模，如图5-6所示。

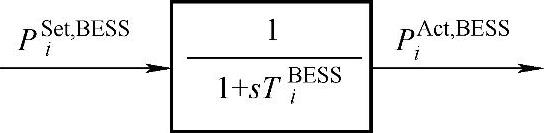
图5-6　电池储能系统PCS等效模型

图中P_i^Set，BESS和P_i^Act，BESS分别为第i个电池储能PCS系统中的运行参考指令和实际输出功率。图5-6中的传递函数可由式（5-13）的系统状态方程进行表述，即

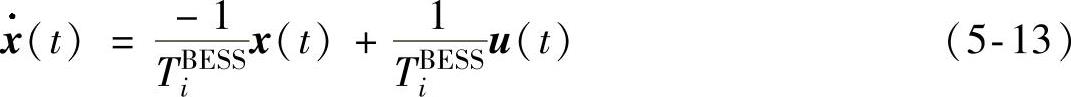
其中系统状态变量x（t）=P_i^Set，BESS（t）和输入变量u（t）=P_i^Act，BESS（t）。电池储能系统PCS系统的动态过程可由上式进行描述。上述建立的PCS系统动态模型可以考虑PCS系统控制指令与系统实际输出之间的时间延迟效应。