电池储能系统在电网调频中的控制实例

储能电池的额定功率P_ES，rated和额定容量E_rated分别为10MW和2.5MWh，其荷电状态Q_SOC的下限Q_SOC，min和上限Q_SOC，max分别为0.2和0.8，对应的储能电池容量下限E_min和容量上限E_max分别为0.5MWh和2MWh。传统电源为火电机组，额定功率P_G.rated为800MW，调频备用容量P_G.cap范围为-40MW～40MW，爬坡速率为24MW/min（3%P_G.rated），其余为小水电机组；电网的惯性时间常数M和负荷阻尼系数D分别取10和0.5。假设0.03pu（基准值1000MW）的小水电机组脱网，仿真时长为250s，依托含有储能电池的区域电网调频动态模展开仿真对比。

1.电池储能系统参与电网一次调频的运行控制实例

假设负荷扰动与电网的惯性时间常数M和负荷阻尼系数D无关，基于此前提，对表4-6。所述两种工况下储能的功率需求进行分析。对于工况1，若需控制Δo₀≥Δo_max，则P_E0应满足如下要求：4.8MW≤P_E0≤30MW；若需控制Δf_m≥Δf_{m_max}，则M₁应不小于10.8s，此处取为10.8s，可得P_E1≥11.4MW；若需控制Δf_qs≥Δf_{qs_max}，则P_E2≥10.344MW。对于工况2，同理可得：3MW≤P_E0≤30MW，M₁应取为11.4s，P_E1≥7.8MW，P_E2≥9.75MW。由于两种工况下所需的储能功率分别为11.4MW和9.75MW，考虑到储能的效率，确定储能的功率需求为12MW。综上可得具体的功率需求见表4-7。

表4-6　电网参考事故和调频评估指标要求

表4-7　储能的功率需求

在表4-7中，以对应工况下的电网额定容量S_BASE为基准，在储能功率需求为12MW的前提下，可得M_E和K_E的取值在工况1中分别为3.8和3.45，在工况2中分别为2.4和3。

基于前述功率需求计算结果展开仿真实验，对比仅含传统电源（Traditional Frequency Regulation，TFR）调频以及传统电源与储能（TFR-ESS）联合调频两种方案，仿真和计算结果分别如图4-23、图4-24和表4-8所示。图中传统电源和储

能的动作深度均以对应工况下的电网额定容量S_BASE为基准。

图4-23　电网引入储能前后的调频结果（工况1）

图4-24　电网引入储能前后的调频结果（工况2）

表4-8　调频评估指标计算结果

对于工况1和工况2，图4-23a和图4-24a为频率偏差Δf（t）曲线。结合表4-8中的初始频差变化率Δo₀、最大频率偏差Δf_m和准稳态频率偏差Δf_qs指标可知，储能的引入显著改善了调频效果，且两种工况下的调频评估指标计算结果均能较好地与理论分析相吻合，从而达到了参考事故下的频率控制要求。其中工况1的Δo₀从-0.0286puHz/s变为-0.0186puHz/s，工况2的Δo₀从-0.0134puHz/s变为-0.01puHz/s，满足了表4-6所述的频差变化率限值Δo_max要求，同时，Δf_m和Δf_qs指标也满足了相应的最大频率偏差限值Δf_m__max和准稳态频率偏差限值Δf_{qs_max}要求。图4-23b和图4-24b为不同工况下仅TFR和TFR-ESS联合调频的动作深度。结合表4-8中的短时贡献电量G_pm和长时贡献电量G_pqs指标可知，相比仅TFR调频，TFR-ESS联合调频的优势在于t₀～t_m时段的G_pm上，而在G_pqs上差距较小，这表明储能的引入在改善调频效果的同时，并未增加太多额外的调频电量需求。图4-23c和图4-24c为不同工况下TFR-ESS联合调频时传统电源和储能各自的动作深度。由图中可知，相比仅TFR调频，此时传统电源的动作深度相对减小，即引入储能可减轻它的调频负担；同时，理论分析得出的12MW储能可较好地满足各工况需求，其最关键的作用是在扰动瞬间提供了峰值功率，避免了初始频差变化率的突变及低频减载的启动，并将准稳态频率偏差控制在要求范围内。

通过对储能在各调频时段内的动作深度进行积分，可得到两种工况下的容量需求结果（包含额定功率与持续时间），见表4-9。

表4-9　储能的容量需求(www.xing528.com)

由表4-9可知，在对应时段选择两种工况下所需容量的较大值，即在t₀～t_m时段内预留12MW×1s、在t₀～t_qs时段内预留12MW×4.3s就能满足调频要求。为了避免储能的深度充放电影响其使用寿命，且保持其在下一调频任务时处于可充和可放的状态（即控制荷电状态Q_SOC接近于运行参考值Q_SOC，ref）并计及PCS的损耗，可得最终的储能容量需求方案为12MW×9s。由于储能具有高倍率放电能力^[120]，即使按上节所配置的10MW储能电池也能满足这两种工况的要求。

2.电池储能系统参与电网二次调频的运行控制实例

其仿真结果分别如图4-25～图4-27、表4-10和表4-11所示。图4-25为频率偏差Δf和区域控制误差信号S_ACE曲线；图4-26为储能的参与因子α和灵敏度S^ES_α曲线；图4-27为储能的动作深度ΔP_ES、传统电源参与二次调频的动作深度ΔP_S、二次调频总动作深度ΔP_total和传统电源参与一次调频的动作深度ΔP_F曲线；表4-10和表4-11分别为与频率和贡献电量相关的指标计算结果。

针对上节所提策略，图4-25a和表4-10显示其结合了基于ACE信号的控制方式分析（以下统一称“模式一”）在抑制最大频率偏差Δf_m、减小达到峰值的时间t_m和降低频率下滑速度V_m上的优势，及基于ARR信号的控制方式分析（以下统一称“模式二”）在减少达到稳态的时间t_s和提高频率恢复速度V_r上的优势，进而使得频率偏差Δf快速恢复至零。由图4-25b同样能得到此分析结果。由图4-26a可看出，它的储能参与因子α值是变化的，在阶段1和阶段2中分别为0.294和0.2，对应的模式切换时刻为第25s；图4-26b显示其使得灵敏度S_α^ES在调频过程中恒小于0，保留了模式一在阶段1和模式二在阶段2的灵敏度特性，避免了模式一因S_α^ES过零而导致的阻碍作用，也较好地发挥了储能的辅助调频作用，间接证明了图4-25a和表4-6分析结果的合理性。

图4-25　频率偏差和区域控制误差信号曲线

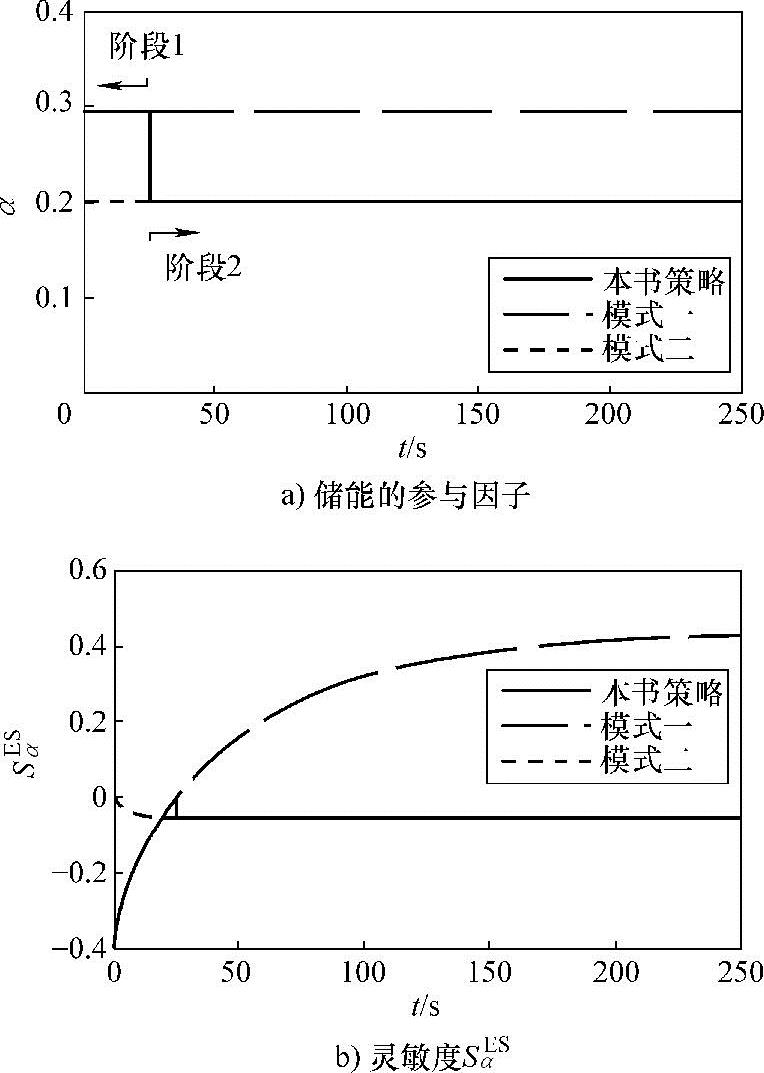
图4-26　储能的参与因子和灵敏度S_α^ES曲线

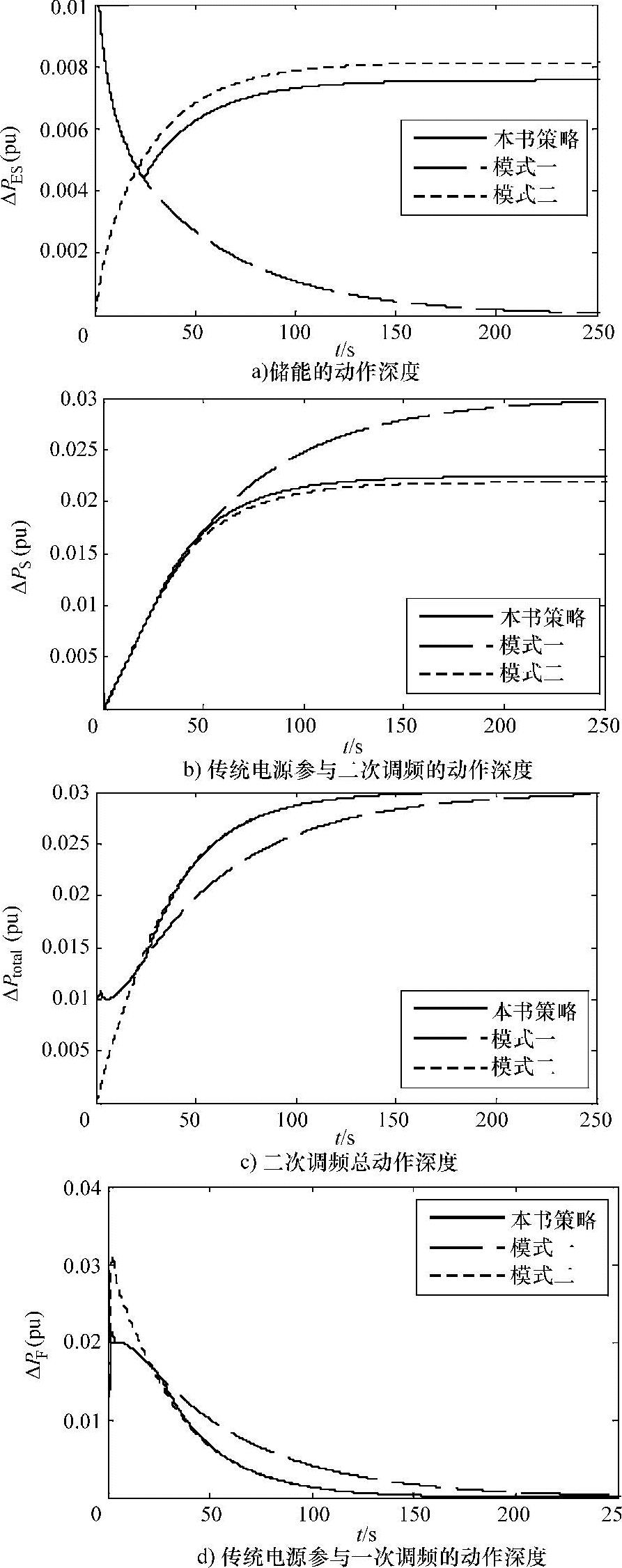
图4-27　ΔP_ES、ΔP_S、ΔP_total和ΔP_F曲线

表4-10　与频率相关指标的计算结果

表4-11　与贡献电量相关指标的计算结果

图4-27a和表4-11中储能的贡献电量G_ES、图4-27b和表4-11的传统电源参与二次调频的贡献电量G_S表明其仅需储能和传统电源释放与模式二相当的能量就能获得更好的调频效果。由图4-27c和表4-11的二次调频总贡献电量G_total指标可看出，它在保证调频效果最佳的前提下，需要的G_total仅稍多于模式二，但明显少于模式一，显著体现了本策略的优越性。由图4-27d和表4-11的传统电源参与一次调频的贡献电量G_F指标可知，它降低了传统电源参与一次调频的贡献电量，减少了相应的调频容量需求。

应当指出，所提策略充分利用了储能的技术优势，使得电网能够更为准确地跟踪调频信号，避免了传统调频中出现的延迟、反向和偏差等现象，能达到有效改善暂/稳态频率质量的目标。同时，它还能提高传统电源的运行效率，节省燃料且减少废气排放，进而带来了更多的间接效益。最后，它还能减少需要购买的调频服务量，避免了由于传统电源对调频信号的不准确响应而导致的高调频容量需求。