电池储能系统在电网调频中的基本控制模式

电网调频又称频率调整或频率控制，是电力系统中维持有功功率供需平衡的主要措施，其根本目的是保证电力系统的频率稳定。电力系统频率调整的主要方法是调整发电功率和进行负荷管理。按照调整范围和调节能力的不同，频率调整可分为一次调频、二次调频和三次调频。其中三次调频就是协调各发电厂之间的负荷经济分配（即有功功率经济分配）；其实质是完成在线经济调度；其目的是在满足电力系统频率稳定和系统安全的前提下合理利用能源和设备，以最低的发电成本或费用获得更多的、优质的电能。三次调频属于电网经济调度问题，本书涉及储能电池参与电网调频控制方法仅就一次调频、二次调频控制策略进行分析，三次调频不做讨论。

1.储能电源参与电力系统一次调频的控制策略

一次调频是指当电力系统频率偏离目标频率时，发电机组通过调速系统的自动反应，调整有功出力以维持电力系统频率稳定。一次调频的特点是响应速度快，但是只能做到有差控制。一次调频主要应对短周期的负荷功率变化导致的电网频率波动，响应迅速，可由储能系统自主完成，实现有差调节。其基本工作原理如图4-13所示。

由图4-13可知，当电网频率值在死区范围（f_d，f_u）内时，默认电网频率正常，PCS不进行调节；当电网频率值在（f_low，f_d）范围内时，PCS根据频率值对应的功率值，对电网补充；当电网频率低于f_low时，PCS以最大功率输出有功功率；当电网频率值在（f_u，f_high）范围内时，PCS根据频率值对应的功率值，对电网吸收有功功率；当电网频率高于f_high时，PCS以最大功率吸收有功功率。具体的出力大小根据对应控制策略进行调整，本书将就几种常规控制策略进行详细介绍。

（1）储能电池参与一次调频下垂控制方法

图4-13　一次调频工作原理图

储能电池参与一次调频的方法如图4-14所示。图中，Δf_db为调频死区，Δf_db_u和Δf_db_d分别为其上、下限值；Δf_u和Δf_d为针对储能电池设置的调频出力上、下限值，频率偏差超过该限值时储能电池以额定功率出力。

由图4-14可知，当负荷突然增加时，负荷频率特性曲线将由L₁（Δf）移至L₂（Δf），由传统电源的功频曲线G（Δf）可知其会自动增加出力，以阻止频率进一步下降，电网运行点将由稳定运行点a移至b点，对应的频率偏差从0下降至Δf₁（其为负值）。此时，利用储能电池模拟传统电源的下垂特性以实现参与一次调频，通过设置储能电池的虚拟单位调节功率K_E，对应储能电池的出力为如图中所示的P_E值。

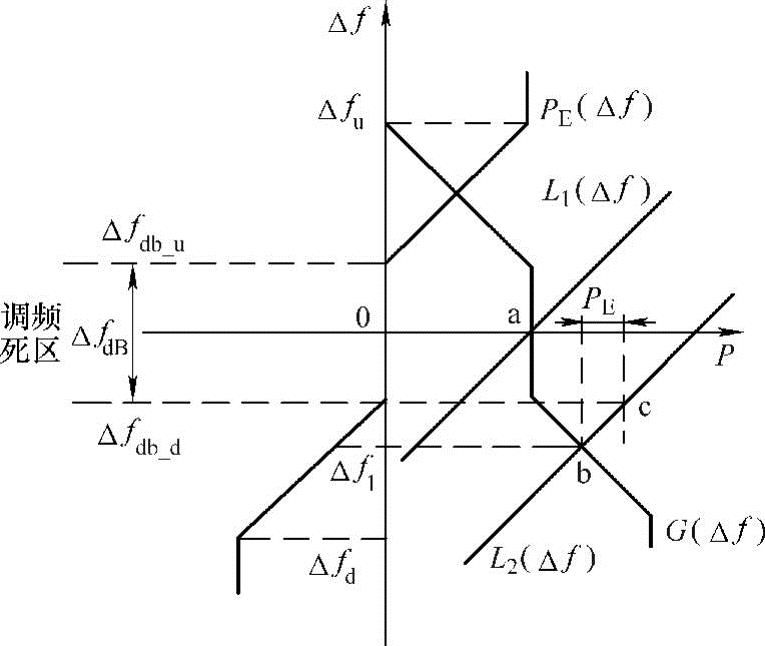
图4-14　储能电池参与一次调频的方法

电网中的传统电源功率或负荷发生变化时，必然会引起电网频率的变化。当电网供电大于负荷需求时，电网频率会上升，此时应控制储能电池从电网吸收功率；当电网供电小于负荷需求时，电网频率会下降，此时应控制储能电池释放功率至电网。

（2）储能电池参与一次调频的改进下垂控制

目前储能电源参与一次调频主要是通过模拟机组的下垂特性，所以需要研究储能电源的功率增量与频率增量之间的内在联系并进行优化控制。根据下垂控制的原理可知，下垂系数的倒数即为单位调节功率。目前大多数文献采用固定的单位调节功率值参与电力一次调频，并取得了一定的效果。但是针对负荷的长时随机小扰动，电池的SOC状态作为储能电源一个非常重要的变量之一，在储能电源控制方法的研究中必须加以考虑。

目前计及储能SOC影响的控制策略的基本思想主要分为两种。一种是如何在调频过程中维持SOC在期望值附近，一般为50%。当储能SOC较高时，储能电源多充电，减少放电；当储能SOC较低时，储能电源多放电，减少充电。另一种则是当储能电源进入调频死区时，如何将SOC恢复到期望值附近。

风险偏好曲线是反映决策者对风险态度的一种曲线。由于调频效果反映了储能电源在技术上的应用效果，而SOC的保持效果反映了储能电源在经济性上的投资风险。正如不同的投资者对风险的态度存在差异，在电力运行过程中，电力系统的不同应用场合同样对调频效果和SOC控制效果存在不同偏好。通过借鉴风险偏好曲线的分类方法，提炼了三种控制策略。按照调频效果和SOC保持效果的偏好，三种控制策略可分为保守型、激进型及混合型。

1）保守型。

图4-15为保守型策略中储能SOC与K_b的关系。图中实线为充电时的单位调节功率，虚线为放电时的单位调节功率。该曲线在SOC限制范围内是下凸的。这意味着，在充电时，一开始K_b将快速下降，随着SOC增加，速度才逐渐减慢。当SOC=0.5时，储能电源处于较低的状态。这种策略更注重对SOC的维持，只有当SOC足够时才允许储能电源充分出力。

为实现负荷功率在分布式储能单元之间的合理分配，提出了基于荷电状态（SOC）改进下垂控制方法。储能电源的保守型控制策略如式（4-17）所示。

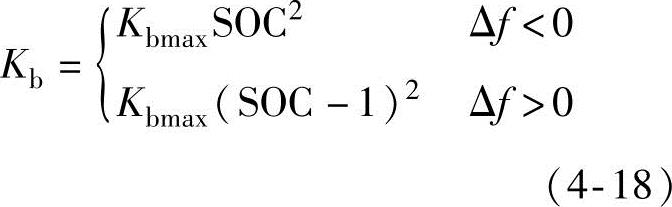
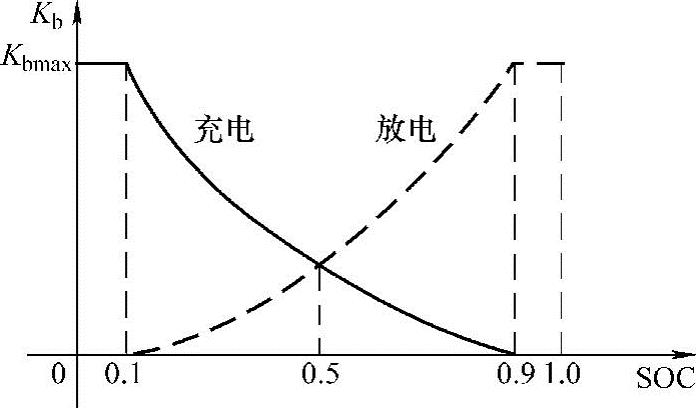
图4-15　保守型控制策略

式中 K_b——电池单位调节功率；

K_bmax——储能电源单位调节功率最大值；

SOC——电池荷电状态实时值；

Δf——频率偏差。

2）激进型。

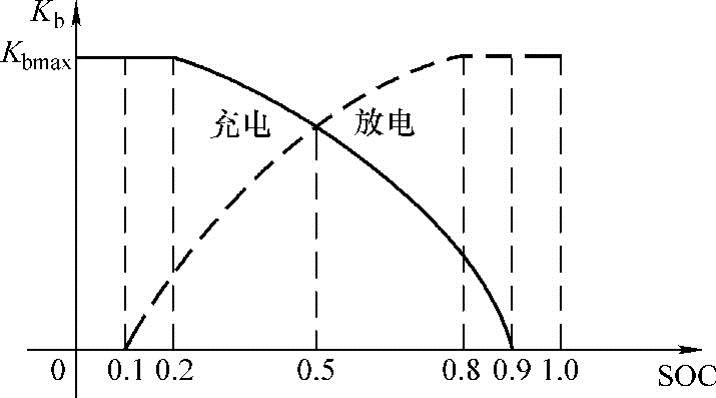
图4-16　激进型控制策略

图4-16中的实线为充电时的单位调节功率，虚线为放电时的单位调节功率。该策略与第一种策略恰恰相反，曲线是上凸的，即在充电期间，当SOC较小时，Kb减少较小且减少速度较慢以提供足够的功率输出。在保证了输出的同时，牺牲了对SOC的保持效果。

根据参考文献[110]提出的一种通过调整充放电功率来保持电池剩余容量的单位调节功率的公式，可得出激进型的控制策略，即

式中　K_b——电池单位调节功率；

K_bmax——储能电源单位调节功率最大值；

SOC——电池荷电状态实时值；

SOC_max、SOC_min、SOC_high、SOC_low——分别为设定的荷电状态的最大值、最小值、

较高值和较低值；

n——方程的幂指数，n可选为2。

K_b按照充电过程和放电过程分为K_c和K_d，其具体控制方式如下

式中

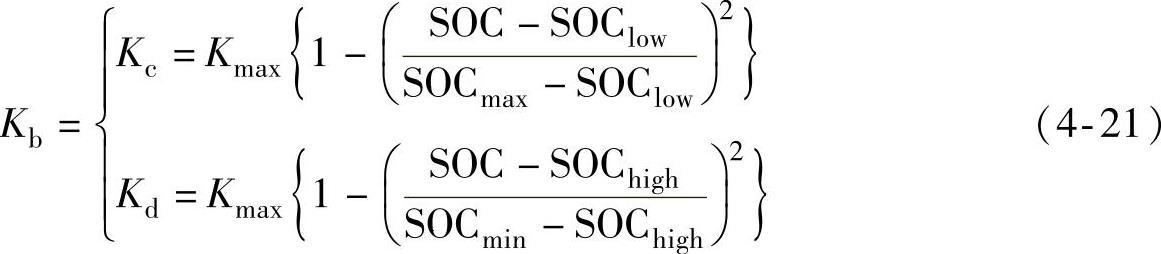(www.xing528.com)

式中　P_V2G——V2G的出力；

K_c——充电时的单位调节功率；

K_d——放电时的单位调节功率。

当期望SOC保持在0.5附近时，SOC_max=0.9、SOC_min=0.1、SOC_high=0.8、SOC_low=0.2。

3）混合型。

在激进型和保守型的基础上，根据参考文献[111]提出的一种新的单位调节功率控制方法可提炼出混合型的控制策略。该策略将SOC进行了分段控制。SOC不同时段的充电单位调节功率和放电单位调节功率不同。

图4-17中的实线为充电时的单位调节功率，虚线为放电时的单位调节功率。粗实线和细实线分别为保持的SOC不同时的单位调节功率曲线。从图中可以看出，该策略结合了以上两种策略。以充电过程为例，当SOC低于期望水平（0.5）时，K_b如激进型策略一样减少以保证输出足够功率；当SOC稍大时，K_b则像保守型一样迅速减小出力以阻止SOC继续增大。

当SOC_i＜SOC₀时，该策略令电池充电时的单位调节功率大于放电时的单位调节功率，从而使电池吸收的功率大于放出的功率，电池的SOC将被迫提升。

同理，SOC_i＞SOC₀时，该策略令电池充电时的单位调节功率小于放电时的单位调节功率，从而使电池吸收的功率小于放出的功率，电池的SOC将被迫下降。

在SOC_min和SOC_max不变时，SOC₀可以随意改变。

图4-17　混合型控制策略

2.储能电池参与二次调频的方法

二次调频也称为自动发电控制（AGC），是指发电机组提供足够的可调整容量及一定的调节速率，在允许的调节偏差下实时跟踪频率，以满足系统频率稳定的要求。二次调频可以做到频率的无差调节，且能够对联络线功率进行监视和调整。二次调频主要应对较长周期的负荷功率变化导致的电网频率波动，通过自动发电量控制（AGC）指令调度储能系统完成，从而实现无差调节，其工作原理如图4-18所示。

由图4-18可知，当电网频率升高时，储能系统通过吸收电网有功功率，给蓄电池充电，使得电网频率恢复到调频死区范围内，调频指令由调度经AGC发送至EMS（能量管理系统），再指派至储能系统及PCS功率变换装置进行控制，而能量则经由电网至PCS在电池储能系统中存储起来。相应地，当电网频率降低时，电池放电，储能系统通过向电网输出有功功率，使得电网频率恢复到调频死区范围内，调频指令由调度经AGC发送至EMS（能量管理系统），再指派至储能系统及PCS功率变换装置进行控制，而能量则经由电池储能系统释放，经PCS功率变换装置进入电网，以维持电网稳定。

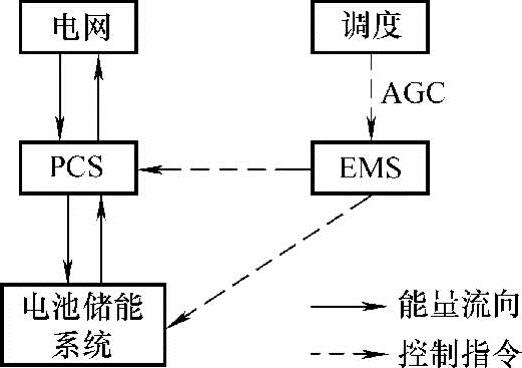
图4-18　二次调频工作原理图

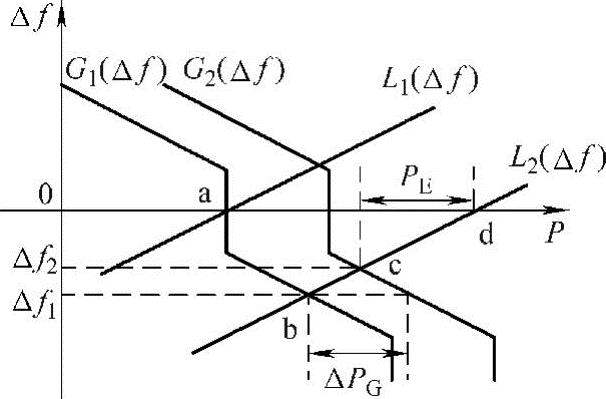
图4-19　储能电池参与二次调频的方法

储能电池参与二次调频的方法如图4-19所示。当负荷突然增加时，负荷频率特性曲线将由L₁（Δf）移至L₂（Δf），当传统电源的一次调频功能启动时，电网运行点将由稳定运行点a移至b点，对应的频率偏差从0下降至Δf₁（其为负值）。当传统电源的二次调频功能启动时，假设其备用容量不足，功率频率曲线将由G₁（Δf）移至G₂（Δf），对应的二次调频出力为ΔP_G，此时电网运行点将由b点移至c点，即频率偏差从Δf₁回升至Δf₂。在此场景下，控制储能电池放电，功率指令为P_E，频率偏差将恢复至0。即传统电源联合储能电池参与二次调频，通过对区域控制误差信号的合理分配，使得传统电源的出力为ΔP_G，储能电池的出力为P_E，最终实现电网频率的无差调节。

（1）基于ARR信号的控制方式分析

在现有研究中，储能电源参与AGC的控制策略为ARR信号的分配方式，相应控制框图如图4-20所示。

图4-20　基于ARR信号分配的控制方式框图

图中，a为储能出力在ARR信号中所占比例系数；1-a为机组二次调频出力在ARR信号中所占比例系数。基于图4-20，可以推导出机组出力、储能电源出力、负荷功率以及系统频率的增量关系如式（4-22）～式（4-24）所示。

频率偏差为

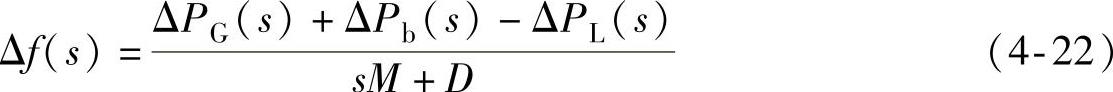
机组出力为

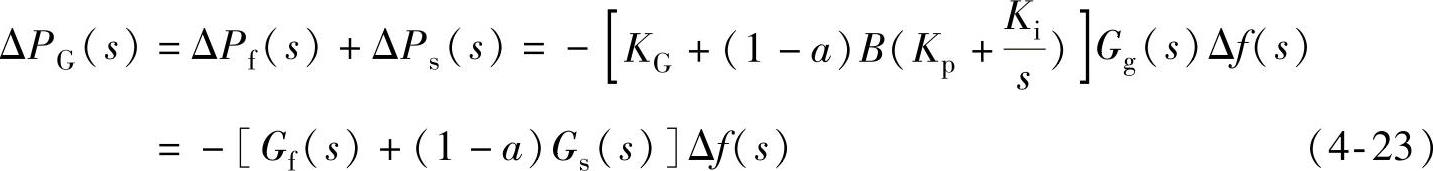
当储能出力不计及SOC影响时，有

式中，G_b（s）——储能电源出力延时。

从式（4-23）和式（4-24）中可看出，在暂态过程中，一次调频量和频率偏差的变化基本一致。由于PI环节的存在，储能电源出力的快速特性被部分抑制，并和机组二次调频量一样保持稳步增长。在稳态时，最终由储能电源和机组二次调频量按比例分担负荷增量，机组一次调频量减小至零。若使用ARR信号作为控制信号，从系统的角度来看，此方法未能很好地利用储能的快速响应能力以优化系统性能。更重要的是，从储能电源容量的角度来看，此方法在保持SOC方面的局限性是显而易见的。

（2）基于ACE信号的控制方式分析

为了克服上节所分析的ARR信号分配方式的缺陷，相对而言的一种基于ACE信号直接分配的控制方式，其控制框图如图4-21所示。

图4-21　基于ACE信号分配的控制方式框图

从图4-21中可以看出，该控制方式与基于ARR信号的控制方式不同之处在于，储能电源的控制信号没有经过PI环节，直接来自于ACE信号，即储能电源出力与ACE信号呈正比关系，可以即时响应ACE的变化。

频率偏差和机组出力的表达式与上节所提表达式一致，但储能电源出力不再经过PI环节，如式（4-25）所示。

ΔP_b（s）=-aBG_b（s）Δf（s） （4-25）

从式（4-25）中可看出，在暂态过程中，储能电源与随着频率偏差变化而增减出力，并避免了PI控制器的延时影响。在发生同一扰动时，相比基于ARR信号的控制方式，储能电源出力减小，机组一次、二次调频量均增加。在稳态时，最终由机组二次调频全部补偿负荷增量，而储能电源出力和一次调频量减小至0。这种控制方式不仅可以保证其快速动作的能力，也可以使储能电源自适应地减小SOC变化。