电池储能系统参与电网调频的容量配置实例

1.面向一次调频的储能电池容量配置实例

本小节以磷酸铁锂储能电池为研究对象，对面向一次调频的储能电池容量配置进行实例分析。表4-1为含有储能区域的电网仿真参数，其中包括区域电网调频动态模型的基本参数以及储能的经济技术参数等，其余与传统电源相关的参数见参考文献[87]。

设调频时段T为30min，采样周期为1s。在实际风电出力P_w的基础上叠加相应时段的负荷功率P_load，则得综合负荷扰动P_c（该调频时段对应的综合负荷扰动是从长时数据中随机选取的非连续样本数据），如图4-6所示（均为以电网额定容量S_BASE为基准的标幺值）。具体仿真步骤如下：

1）设置储能的调频死区与传统电源相同。将综合负荷扰动接入区域电网调频动态模型，经传统电源一次调频后的频率偏差信号Δf如图4-7所示。由图中可知，此时的最大频率偏差为0.55Hz。

表4-1　含储能的区域电网仿真参数

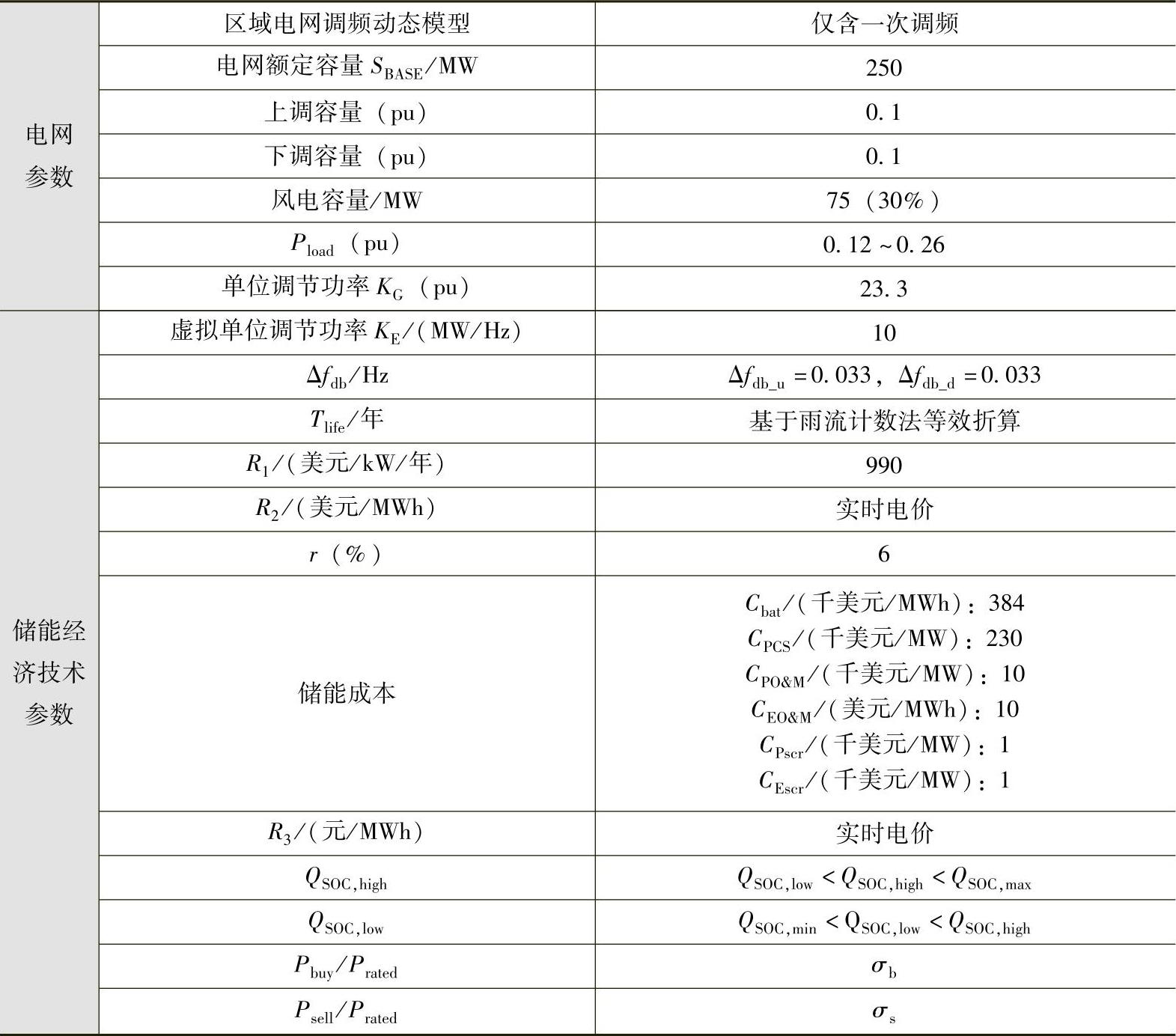
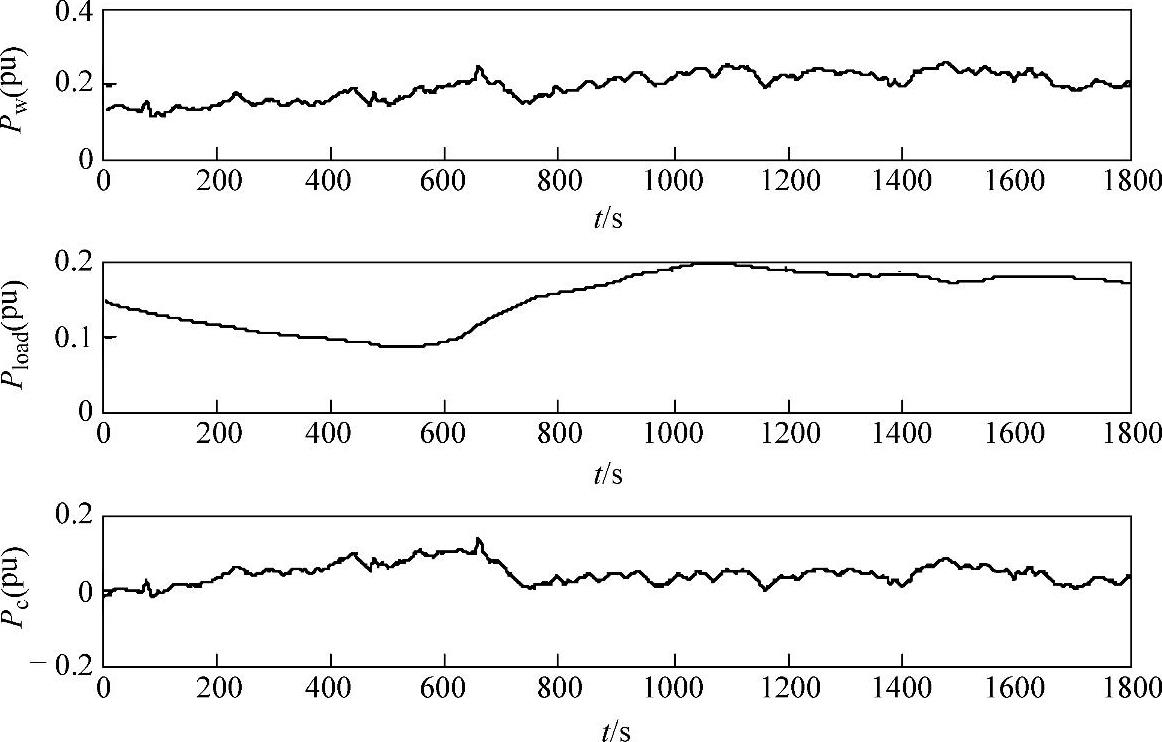
图4-6　风电出力、负荷功率及综合负荷扰动曲线

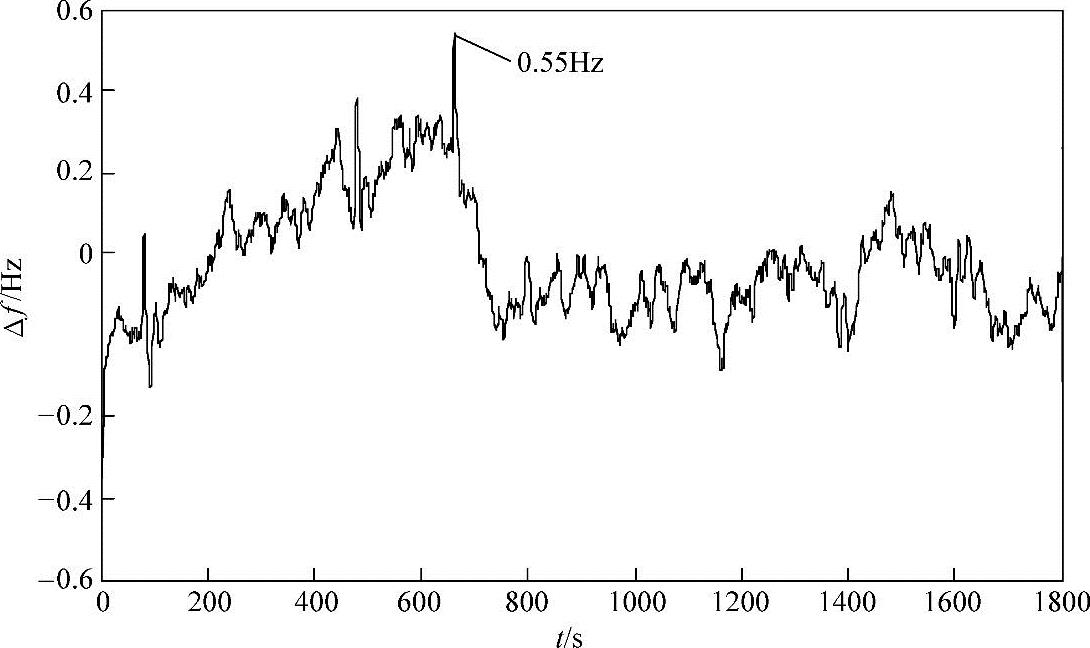
图4-7　电网频率偏差信号

2）基于储能参与一次调频的充放电策略，分别以一次调频效果最优，经济性最优和两者综合最优为目标，对控制变量Q_SOC，high、Q_SOC，low、P_buy（即σ_bP_rated）和P_sell（即σ_sP_rated）进行寻优。

3）根据优化得到的控制变量值，及对应的电网频率偏差，储能在调频死区内有/无额外充放电时的功率指令曲线如图4-8所示。确定储能额定功率P_rated的优化范围的方法如下：因储能在调频过程中需要对频率偏差相对应的储能功率指令进行完全跟踪，故P_rated的取值应考虑最大频率偏差对应的功率指令值，同时还需计及储能本身的运行特性。在本工况下储能的最大出力值对应为5.5MW（最大频率偏差与虚拟单位调节功率之积），同时，考虑到维持储能自身运行一般约需15%P_rated，及一定的功率裕量，故确定其优化范围为5.5～11MW。进而通过寻得的最优控制变量可计算出相应的储能额定容量E_rated、一次调频效果评价指标J₁、成本现值C_LCC、净效益现值P_NET、储能的等效循环寿命T_life等经济评价指标。

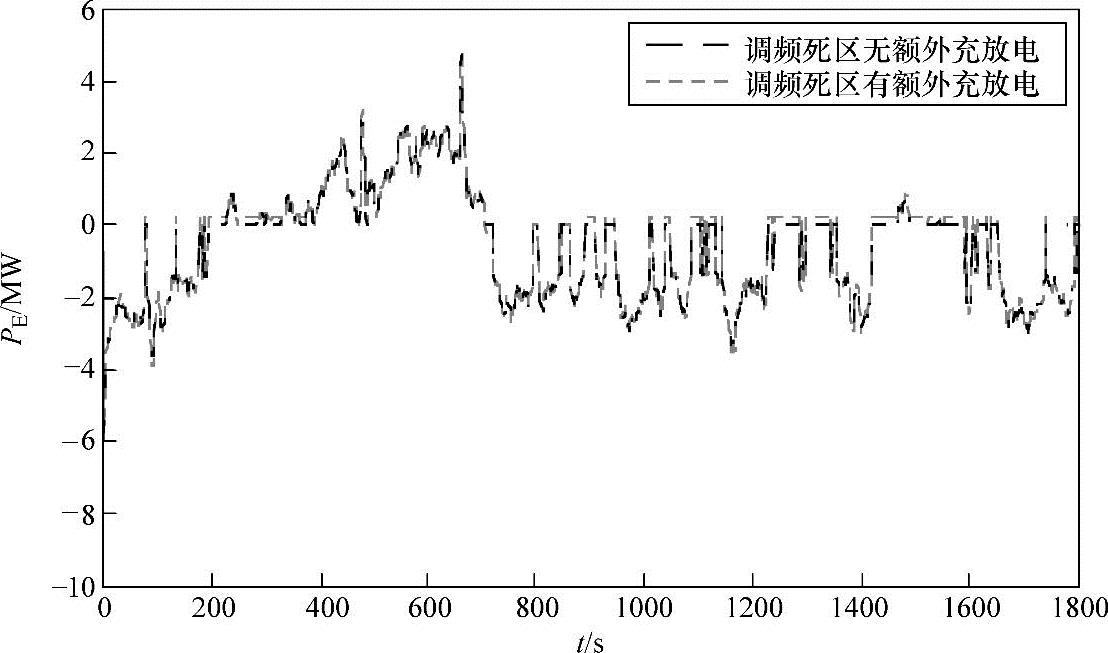
图4-8　储能的功率指令曲线

设置储能荷电状态Q_SOC的允许范围为0.1～0.9，即Q_SOC，min=0.1，Q_SOC，max=0.9，当储能在调频死区内不动作时，其荷电状态Q_SOC及能量E_ESS的变化曲线如图4-9所示。

在图4-9中，由荷电状态Q_SOC曲线可知，在调频时段内，从总体趋势来看储能处于放电模式。当在调频死区范围内储能不进行额外充放电时，可得所需的储能额定容量E_rated为0.32P_rated·h；当为增大一次调频效果或增加调频净效益现值而改变储能的充放电策略时，则会造成相应的储能配置容量发生变化。

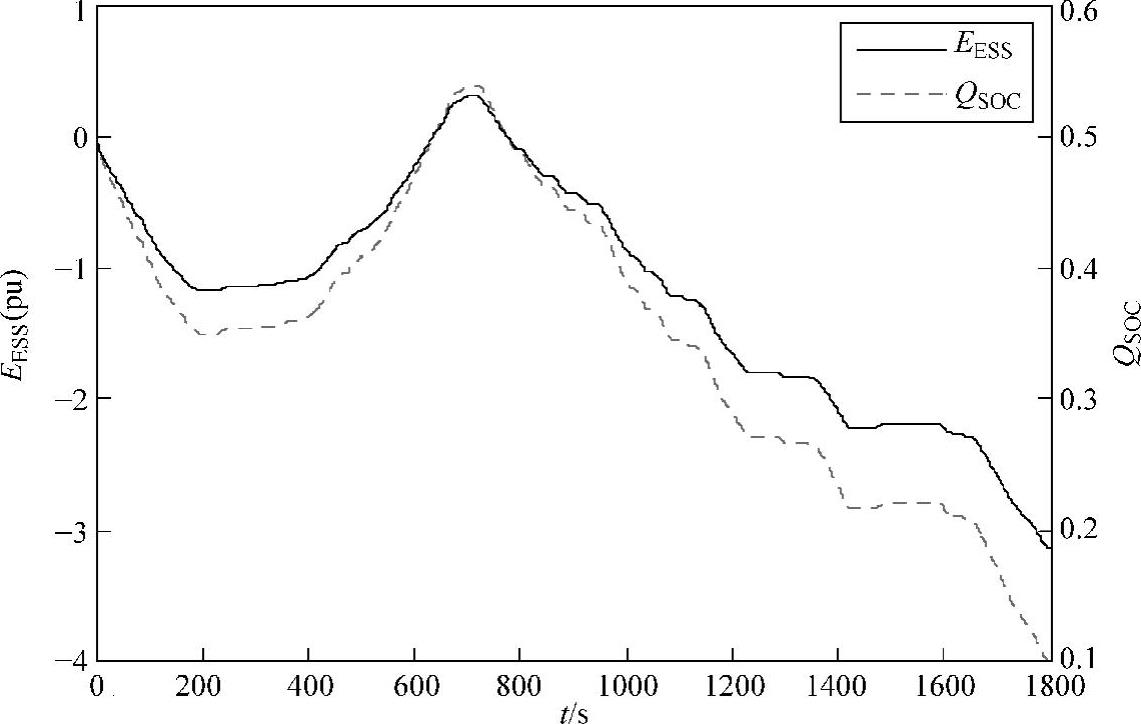
图4-9　调频死区内储能不动作时的荷电状态及能量变化曲线

（1）一次调频效果最优

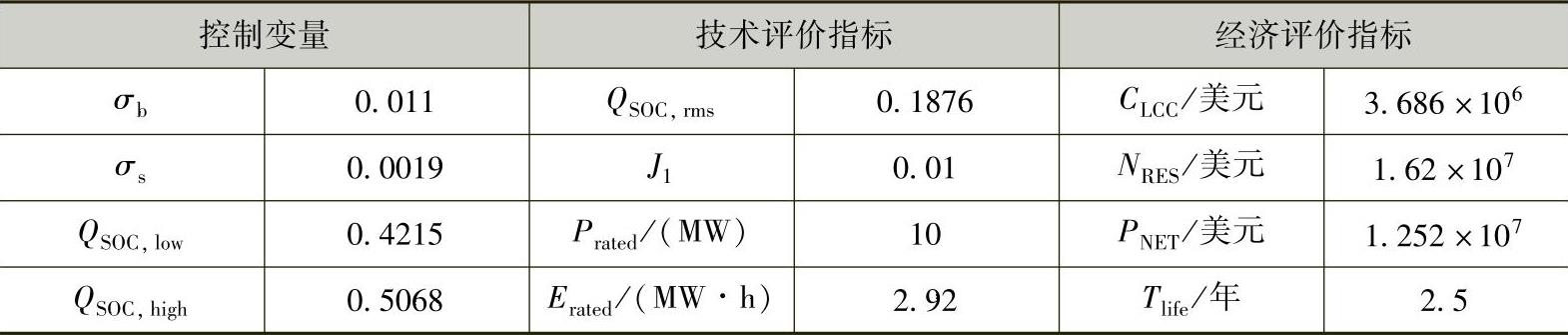
假设全寿命周期T_LCC为20年，依据电网最大频率偏差并考虑储能的运行特性和功率备用，确定储能的额定功率优化范围，再通过寻优得到储能的最优额定功率P_rated为10MW。依据储能在调频过程中的荷电状态Q_SOC变化曲线，利用雨流计数法计算出其等效循环寿命T_life，同时依据经济评估模型计算出全寿命周期内的成本现值C_LCC和效益现值N_RES。以一次调频效果评价指标J₁最小为优化目标，得出的控制变量及技术和经济评价指标结果见表4-2（将储能的额定功率P_rated和额定容量E_rated纳入技术评价指标内）。

表4-2　基于一次调频效果最优的仿真计算结果

（2）经济性最优

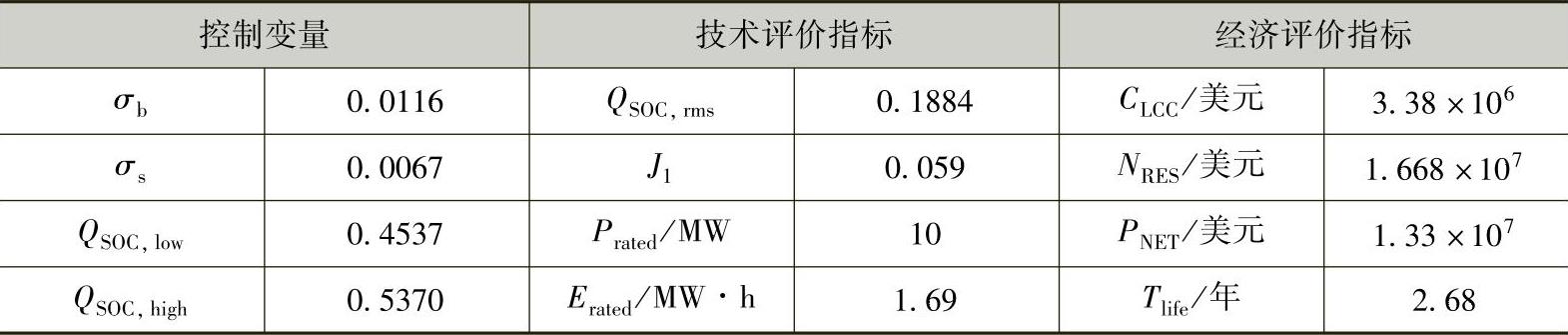
基于同样的储能额定功率P_rated和全寿命周期T_LCC，在满足调频控制要求及储能运行要求约束下，以净效益现值P_NET最大为目标，得出的控制变量及技术和经济评价指标结果见表4-3。

表4-3　基于经济性最优的仿真计算结果

（3）一次调频效果和经济性综合最优

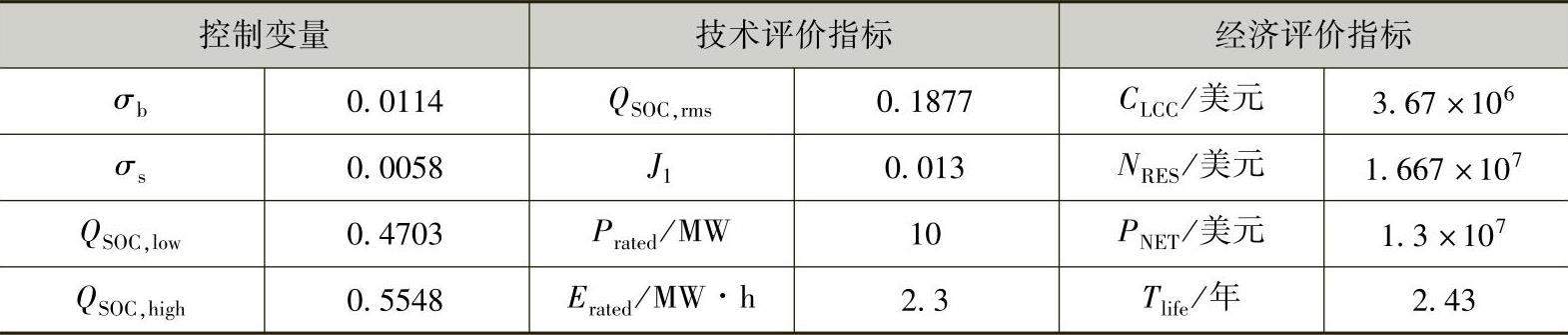
基于同样的储能额定功率P_rated和全寿命周期T_LCC，在满足调频控制要求及储能运行要求约束下，基于一次调频效果评价指标J₁和净效益现值P_NET综合最优的目标，其中把J₁与P_NET折算至同样数量级并赋予相同的权重0.5，优化得到储能的容量配置方案，对应的控制变量及技术和经济评价指标结果见表4-4。

表4-4　双目标综合最优的仿真计算结果

(www.xing528.com)

（4）分析与讨论

1）单目标优化下的技术评价指标对比分析。

当频率偏差处于调频死区-0.033～0.033Hz范围内时，依据储能荷电状态Q_SOC的动作限值（较低值Q_SOC，low和较高值Q_SOC，high）控制储能进行适当的额外充放电，以一次调频效果评价指标J₁最优为目标的充放电策略计算得到的储能容量为0.292P_rated·h，J₁为0.01；以净效益现值P_NET最优为目标的充放电策略计算得到的容量为0.169P_rated·h，J₁为0.059。对比各项参数可知，储能的成本主要由其容量成本决定，基于经济性最优的充放电策略减少了储能的配置容量值，但其会导致调频效果变差。

2）单目标优化下的经济评价指标对比分析。

以20年为储能的全寿命周期，一年以300天工作计算，以一次调频效果评价指标J₁为目标的充放电策略对应的储能的成本现值C_LCC为3.686×10⁶美元，净效益现值P_NET为1.252×10⁷美元；以经济性最优为目标的储能充放电策略，其C_LCC为3.38×10⁶美元，P_NET为1.33×10⁷美元。对比各项参数可知，基于一次调频效果评价指标J₁为优化目标的储能充放电策略所需的容量较大，因而对应的储能成本较高，经济性降低。

3）双目标优化下的评价指标分析。

以一次调频效果评价指标J₁和净效益现值P_NET为双目标的充放电策略计算得到的储能容量为0.23P_rated·h，J₁为0.013，成本现值C_LCC为3.67×10⁶美元，P_NET为1.3×10⁷美元。由表4-4各项优化指标和计算结果可以看出，相比单目标优化得到的目标值，其一次调频效果和经济性得到了一定程度的平衡。

2.面向二次调频的储能电池容量配置实例

基于表4-1中含储能的电网仿真参数，在区域电网调频动态模型中加入二次调频功能模块^[31]，展开相应的仿真实验。其步骤如下：

1）将由风电出力和负荷组成的综合负荷扰动接入区域电网调频动态模型，实时获取的电网区域控制误差信号S_ACE（以电网额定容量为基准值进行标幺化），如图4-10所示。设置调频时长为1天，信号采样周期为1min。

2）利用EMD方法对实时S_ACE信号进行分解，忽略残余分量，可得到信号频率由高至低的不同频段本征模态分量IMF1～IMF9，如图4-11所示。

对S_ACE信号的各频段分量IMF1～IMF9进行傅里叶分析，得到相应分量所属频段的频谱特征如图4-12所示。由图中可知，若以IMF4为分界分量，其波动频率集中于0.5×10^-3Hz，则IMF1～IMF3的频率范围为（0.5×10^-3～8×10^-3Hz）；IMF4～IMF9的频率范围为（0～0.5×10^-3Hz）。

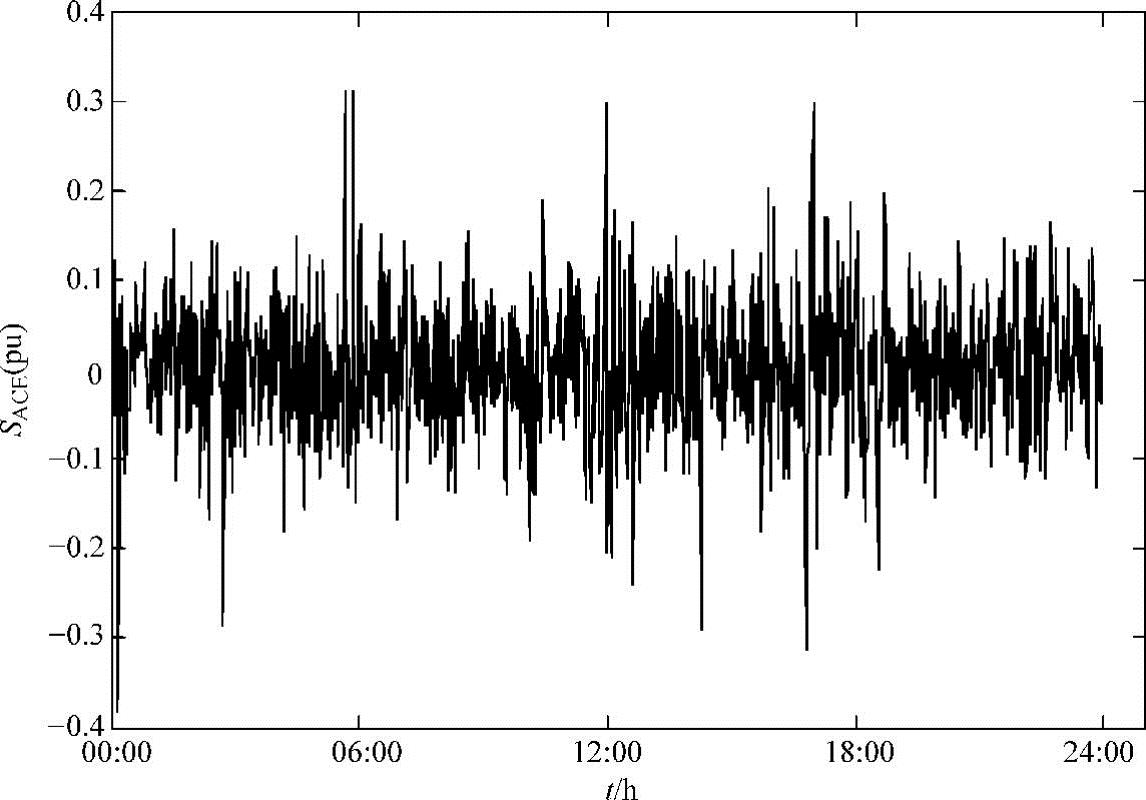
图4-10　实时区域控制误差信号曲线

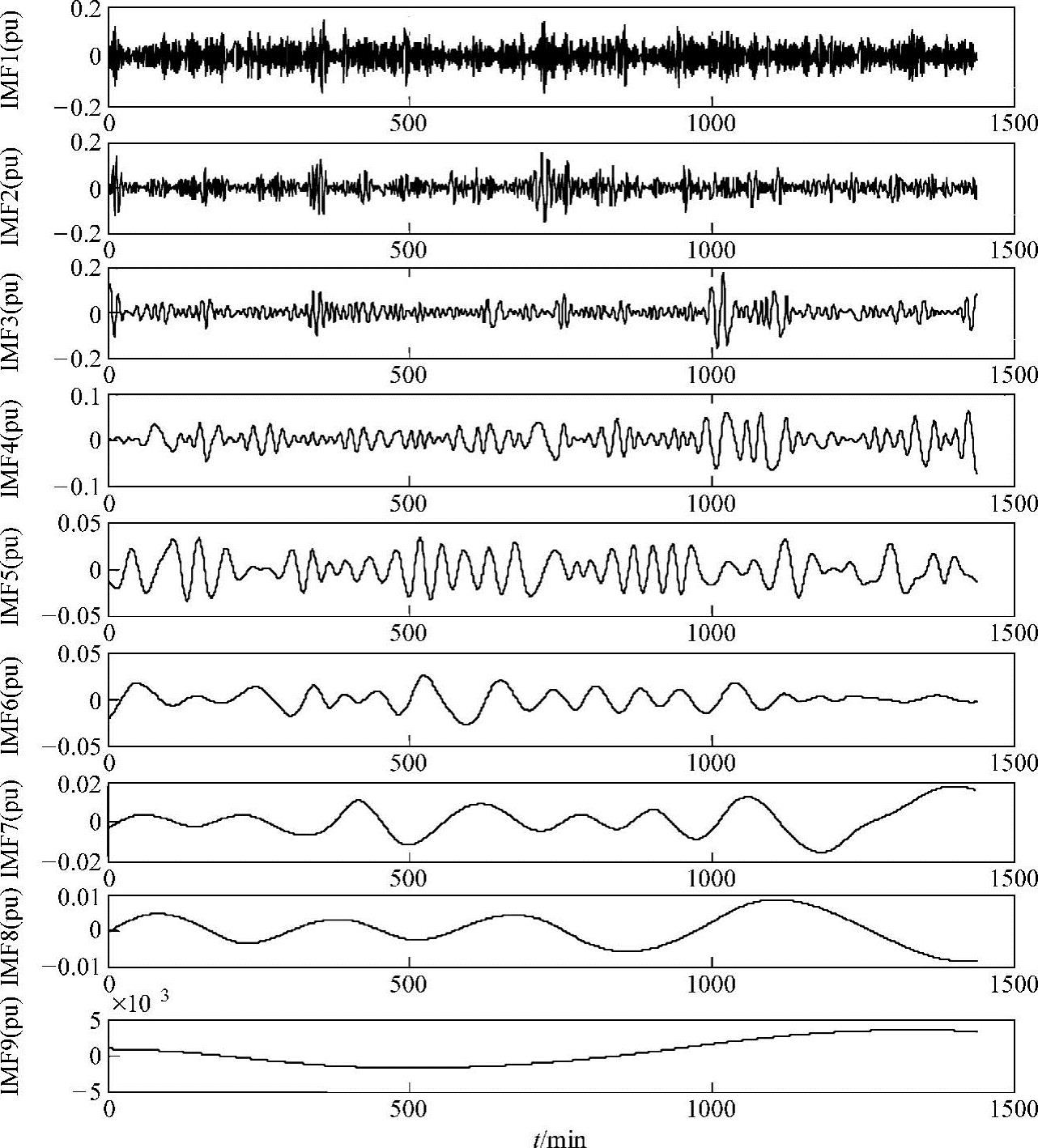
图4-11　经EMD方法分解后的区域控制误差信号各频段分量

3）以二次调频效果最优（即评价指标J₂最小）或净效益现值P_NET最大为优化目标来选择不同分界频率，将分界频率以上频段的区域控制误差信号S_ACE分量分配给储能，分界频率及其以下频段的S_ACE信号分量分配给传统电源，并配置所需的储能容量。

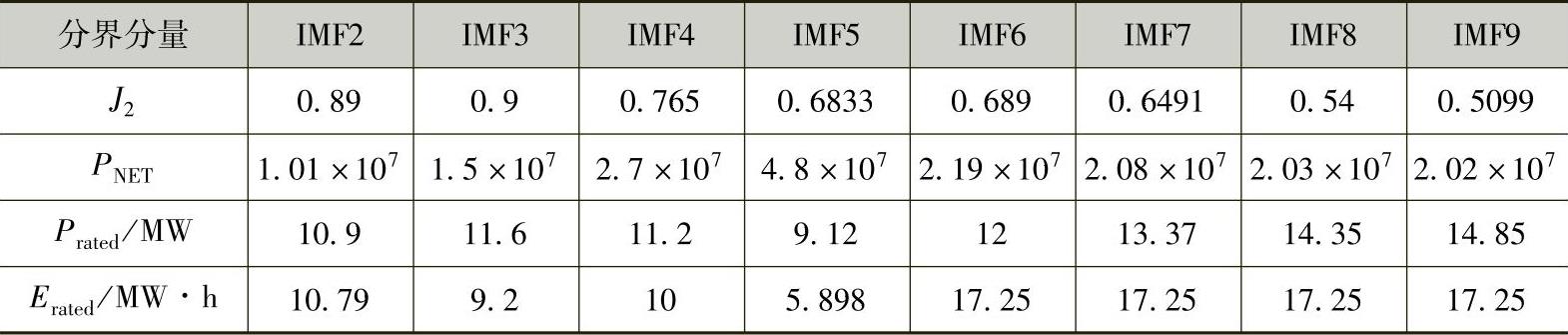
通过以不同本征模态分量作为分界（若采用IMF1，则包括IMF1在内的所有分量均由传统电源承担，储能不参与二次调频，故表中未列出；若以IMF9作为分界分量时，则全部S_ACE信号均由储能承担）计算得到储能的容量配置、二次调频效果评价指标J₂以及净效益现值P_NET，见表4-5。

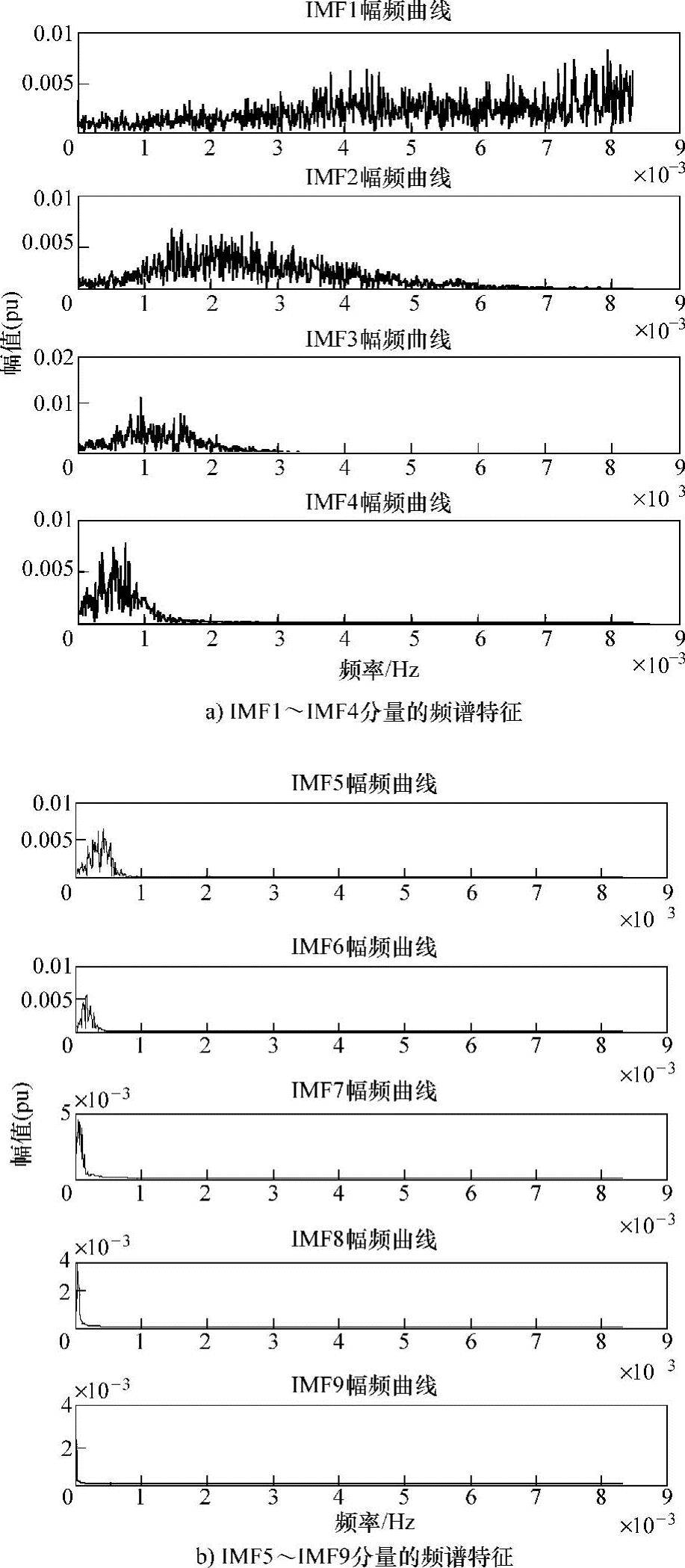
图4-12　区域控制误差信号的各频段分量的傅里叶分析结果

表4-5　不同分界分量下的评价指标及配置方案计算结果

（1）储能分担不同频段区域控制误差信号分量时的二次调频效果评价指标J₂比较

由表4-5可知，以IMF3为分界时，将IMF1～IMF2（1×10^-3～8×10^-3Hz）分配给储能，将IMF3～IMF9（0～1×10^-3Hz）分配给传统电源，计算得到的J₂为0.9，二次调频效果最优，对应的储能额定功率P_rated为11.6MW，额定容量E_rated为0.79P_rated·h。随着储能承担分量的增多及分量频率范围的增大，J₂逐渐降低，这表明容量有限的储能适宜承担S_ACE信号频率较高的分量。

（2）储能分担不同频段区域控制误差信号分量时的调频净效益P_NET比较

以IMF5为分界时，将IMF1～IMF4（0.5×10^-3～8×10^-3Hz）分配给储能，IMF5～IMF9（0～0.5×10^-3Hz）分配给传统电源，得到的P_NET为4.8×10⁷美元，调频经济性最优，对应的储能额定功率为9.12MW，额定容量为0.65P_rated·h。以IMF5为分界，随着储能承担分量的增多及分量频率范围的增大，P_NET逐渐减小。这表明从当前储能的经济性来看，储能也更适宜承担较高频的S_ACE信号分量，因为随着充放电幅值增大，储能的功率和容量成本就会增加，将超过因此带来的经济效益，从而导致经济性降低。

（3）储能分担不同频段S_ACE信号分量时的容量配置方案比较

随着储能承担分量的增多及分量频率范围的增大，储能所需的额定功率和容量基本呈增大趋势（由于存在S_ACE信号的正负叠加，故非完全增大趋势）。以IMF6为分界分量时，储能的容量值将达到稳定，不再变化。这是由于低频分量对应的S_ACE信号幅值较小，各分量累加分配给储能后对其能量影响不大的缘故。