线性分组码的基本原理解析

我们把建立在代数学基础上的编码称为代数码。在代数码中，常见的是线性码。线性码中信息位和监督位是由一些线性代数方程联系着的，或者说，线性码是按一组线性方程构成的。本节将以汉明（Hamming）码为例说明线性分组码的一般原理。

汉明码是一种能够纠正一位错码且编码效率较高的线性分组码。下面介绍汉明码的构造原理。一般说来，若码长为n，信息位数为k，则监督位数r=n-k。如果希望用r个监督位构造出r个监督关系式来指示一位错码的n种可能位置，则要求

2^r-1…n或者2^r…k+r+1 （6-1）

下面通过一个例子来说明如何具体构造这些监督关系式。

设分组码（n，k）中k=4。为了纠正一位错码。由式（6-1）可知，要求监督位数r…3。若取r=3，则n=k+r=7。用a₆，a₅，…，a₀表示这7个码元，用S₁，S₂，S₃表示三个监督关系式中的校正子，则S₁、S₂、S₃的值与错码位置的对应关系可以规定为表6-1所列形式（当然，也可以规定成另一种对应关系，这不影响讨论的一般性）。

表6-1 S₁、S₂、S₃的值与错码位置的对应关系

由表中规定可见，仅当一错码位置在a₂、a₄、a₅或a₆时，校正子S₁为1；否则S₁为0。这就意味着a₂、a₄、a₅和a₆四个码元构成偶数监督关系，即

S₁=a₆⊕a₅⊕a₄⊕a₂ （6-2）

同理，a₁、a₂、a₅和a₆构成偶数监督关系，即

S₂=a₆⊕a₅⊕a₃⊕a₁ （6-3）

以及a₀、a₃、a₄和a₆构成偶数监督关系，即

S₃=a₆⊕a₄⊕a₃⊕a₀ （6-4）

在发送端编码时，信息位a₆、a₅、a₄和a₃的值取决于输入信号，因此它们是随机的。监督位a₂、a₁和a₀应根据信息位的取值按监督关系来确定，即监督位应使以上三式中S₁、S₂和S₃的值为零（表示编成的码组中应无错码）

由上式经移项运算，解出监督位为

给定信息位后，可直接按上式算出监督位，其结果如表6-2所列。

表6-2 信息位与监督位对应表

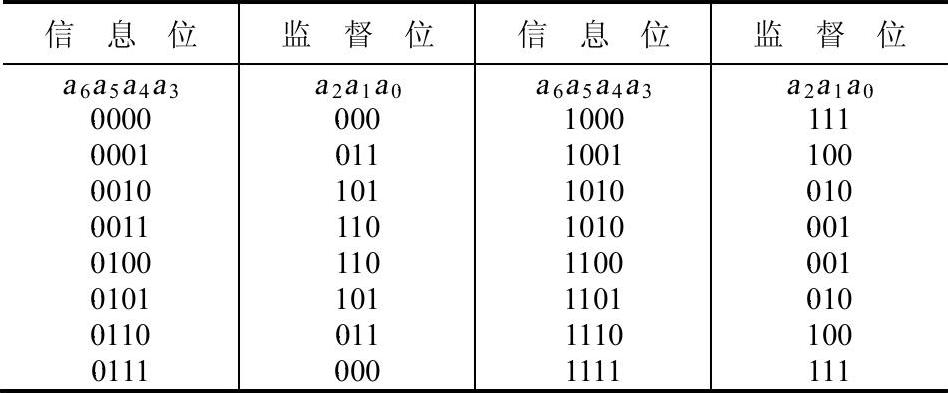
接收端收到每个码组后，先按式（6-2）～式（6-4）计算出S₁、S₂和S₃，再按表6-2判断错码情况。例如，若接收码组为0000011，按式（6-2）～式（6-4）计算可得：S₁=0，S₂=1，S₃=1。由于S₁S₂S₃等于011，故根据表6-1可知在a₃位有一错码。按上述方法构造的码称为汉明码。

现在再来讨论线性分组码的一般原理。上面已经提到，线性码是指信息位和监督位满足一组线性方程的码。式（6-5）就是这样一组线性方程的例子。现在将它改写成

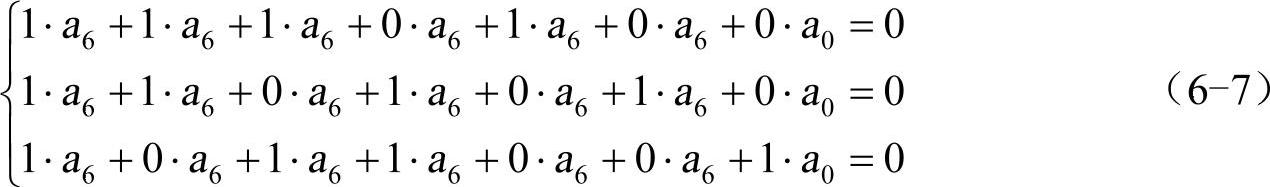
上式中已将“⊕”简写为“+”。在本章后面，除非另加说明，这类式中的“+”都指模2加。式（6-7）可以表示成如下矩阵形式：

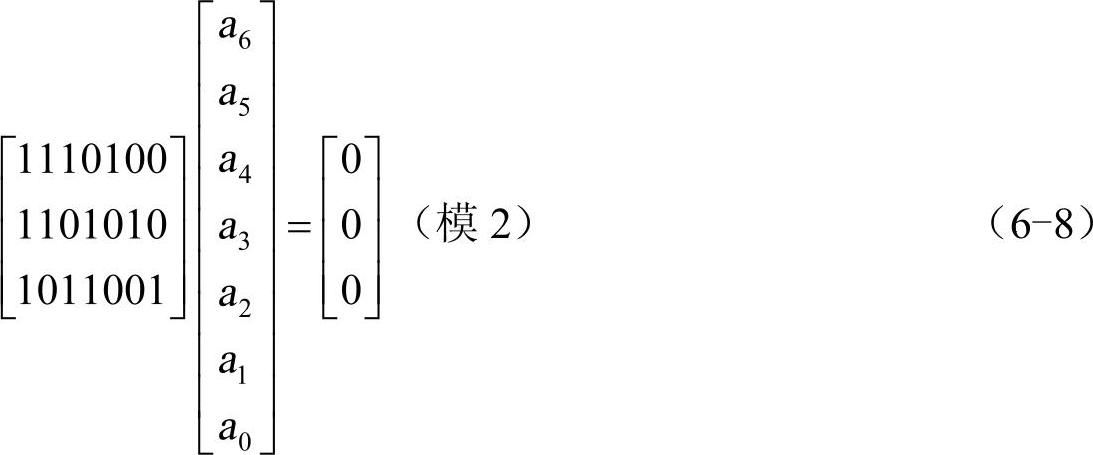
上式还可以简记为

H⋅A^T=O^T或A⋅H^T=O （6-9）

其中

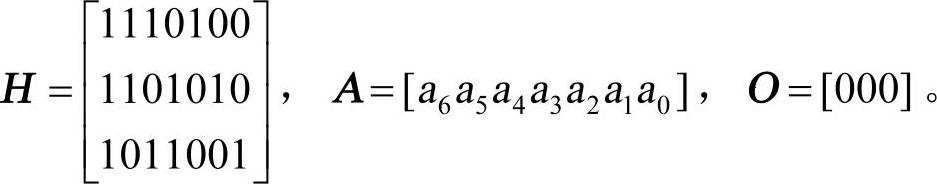
右上标“T”表示将矩阵转置。

将H称为监督矩阵。只要监督矩阵H给定，编码时监督位和信息位的关系就完全确定了。由式（6-7）、式（6-8）都可看出，H的行数就是监督关系式的数目，它等于监督位的数目r。H的每行中“1”的位置表示相应码元之间存在的监督关系。例如H的第一行1110100表示监督位a₂是由信息位a₆a₅a₄之和决定的。式（6-8）中的H矩阵可以分成两部分，即

式中，P为r×k阶矩阵；I_r为r×r阶单位方阵，将具有[PI_r]形式的H矩阵称为典型监督矩阵。

由代数理论可知，H矩阵的各行应该是线性无关的，否则将得不到r个线性无关的监督关系式，也就得不到r个独立的监督位。若一矩阵能写成典型监督矩阵形式[PI_r]，则其各行一定是线性无关的。因为容易验证[I_r]的各行是线性无关的，故[PI_r]的各行也是线性无关的。

类似于将式（6-5）改写成式（6-8）中矩阵形式那样，式（6-14）也可以改写成矩阵形式(www.xing528.com)

或者

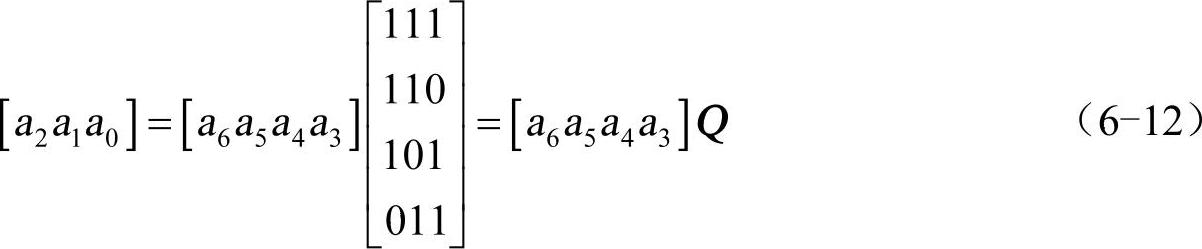
式中，Q为k×r阶矩阵，它为P的转置，即

Q=P^T （6-13）

式（6-12）表明，信息位给定后，用信息位的行矩阵乘以矩阵Q就产生出监督位。

将Q的左边加上一k×k阶单位方阵就构成一矩阵G

G称为生成矩阵，因为由它可以产生整个码组，即

[a₆a₅a₄a₃a₂a₁a₀]=[a₆a₅a₄a₃]⋅G （6-15）

或者

A=[a₆a₅a₄a₃]⋅G （6-16）

一般来说，式（6-16）中A为一n列的行矩阵。此矩阵的n个元素就是码组中的n个码元，所以发送的码组就是A。此码组在传输中可能由于干扰引入差错，故接收码组一般与A不一定相同。若设接收码组为一n列的行矩阵B，即

B=[b_n-1b_n-2L b₀] （6-17）

则发送码组和接收码组之差为

B-A=E（模2） （6-18）

它就是传输中产生的错码行矩阵

E=[e_n-1e_n-2L e₀] （6-19）

其中

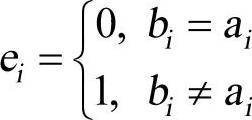
因此，若e_i=0，则表示该位接收码元无错；若e_i=1，则表示该位接收码元有错。式（6-18）也可以改写成

B=A+E （6-20）

例如，若发送码组A=[1000111]，错码矩阵E=[0000100]，则接收码组B=[1000011]。错码矩阵有时也称为错误图样。

接收端译码时，可将接收码组B代入式（6-9）中计算。若接收码组中无错码，即E=0，则B=A+E=A，把它代入式（6-9）后，该式仍成立，即

B⋅H^T=O （6-21）

当接收码组有错时，E≠0，将B代入式（6-9）后，该式不一定成立。在错码较多，已超过这种编码的检错能力时，B变为另一许用码组，则式（6-21）仍能成立。这样的错码是不可检测的。在未超过检错能力时，上式不成立，即其右端不等于零。假设这时式（6-21）的右端为S，即

B⋅H^T=S （6-22）

将B=A+E代入式（6-22）中，可得

S=（A+E）⋅H^T=A⋅H^T+E⋅H^T

由式（6-9）可知

A⋅H^T=0

所以

S=E⋅H^T （6-23）

式中，S称为校正子，有可能利用它来指示错码位置。这一点可以直接从式（6-23）中看出，S只与E有关，而与A无关，这就意味着S与错码E之间有确定的线性变换关系。若S和E之间一一对应，则S将能代表错码的位置。