dsPIC实现载波同步的方法优化为：dsPIC实现载波同步的方法

科斯塔斯环实现的关键是找到本地载波与接收信号载波的相差，由于接收信号被调制过，即每个符号的相位与被调制信息相关，这样为了获得准确的相位差，就需要设法消除信息调制的影响。能否避开这个问题呢？在我们设计的差分调制系统中是可以避开这个问题的。因为差分系统是用相邻符号的相位差来携带调制信息的，因此其载波同步不需要严格的相位同步，只要本地载波与接收信号的载波同频就可以了，它们之间允许存在一个固定的相差。另一方面，接收信号即便是被调制过的，每个符号内载波的相位是不同的，但是其载波频率是固定的。如果前后符号之间的绝对相位不同，按理说由于相位的突变，频率也会发生突变。但是参考图4-12，可以看出如果相邻符号的绝对相位发生了变化，那么过渡点的信号幅度会很小，这样对频率估计的影响就可以忽略了。因此，如果仅对频率进行锁定，而允许一个固定相差的存在，那么载波同步的过程中，就不再需要设法消除调制的影响了。

参见图4-15中解调器的框图，其中载波恢复部分输出的信号采样率是8000采样/s，即恢复的载波信号输出间隔是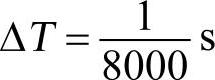，每个采样信号间隔内载波恢复电路令相位增加一个∆ϕ，这样其输出的载波频率就是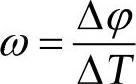。载波恢复电路的功能就是正确地估计出这个∆ϕ，令其输出的载波频率ω与接收信号的载波同频。

根据式（5-1）和式（5-2）的分析，图4-15中低通滤波器B的输出信号可以表示为

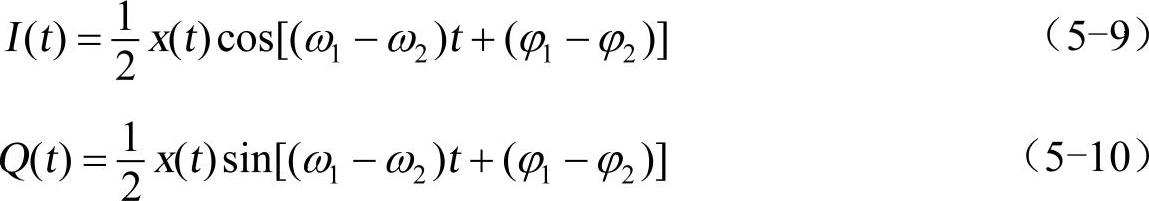
可令Φ表示这个输出信号的相位，即

Φ=（ω₁-ω₂）t+（ϕ₁-ϕ₂） （5-11）

则本地载波与接收信号的频差就可以表示为

根据图4-15中低通滤波器B的输出来计算频差的过程如下：

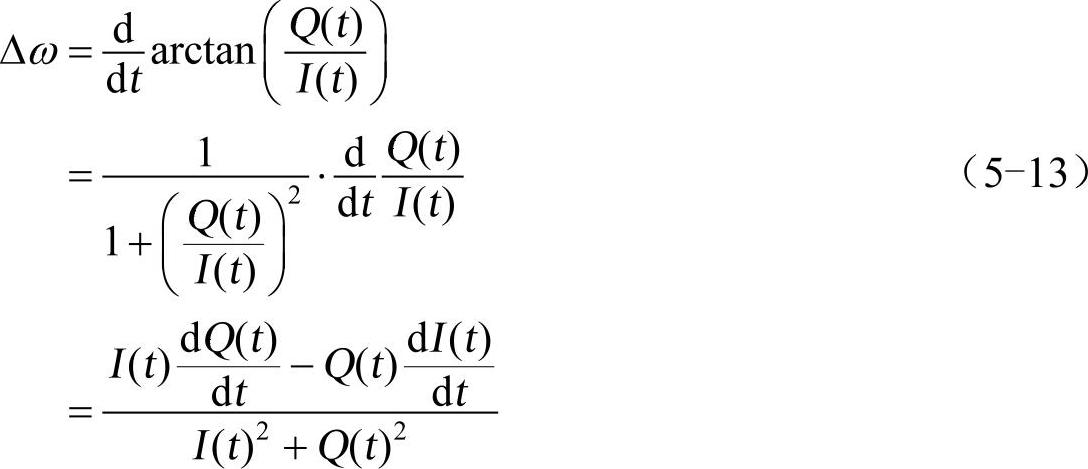
如果用式（5-13）来计算频差，在信号比较小的时候，会得到很大的误差。为了避免这个问题，解调器的AGC电路做了如下处理。当信号幅度比1大时，令信号除以平均幅度，即载波恢复电路的输入的平均幅度接近1，或者说I（t）2+Q（t）2≈1。当信号幅度小于1时，AGC电路不对信号进行处理，这时，如果直接使用式（5-13）来计算∆ω，误差仍然会很大，而且信号幅度小的时候正是绝对相位不同的相邻符号切换的时刻，此时的频差也会出现较大的误差。因此，仍然令I（t）2+Q（t）2≈1，这样计算出来的∆ω就会变得比较小，因而对频率恢复影响就会很小，从而保证了系统的稳定性。综上所述，可以用下面的式子来计算频差：

(www.xing528.com)

载波恢复部分的框图如图5-3所示。

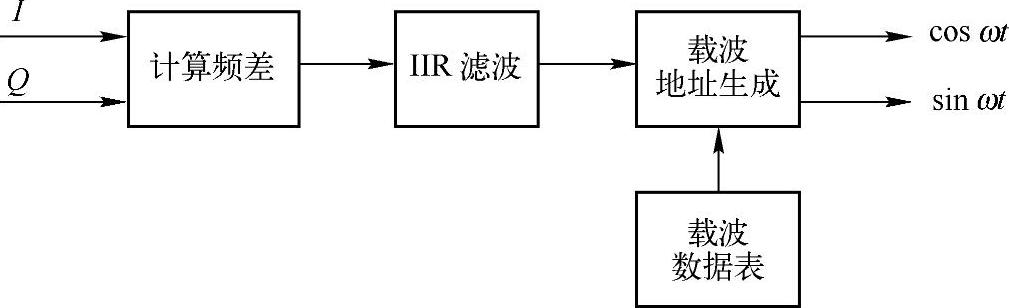
图5-3 载波恢复框图

式（5-14）是模拟信号的计算方法，对于数字系统来说实现方法稍有不同，所采用的公式如下：

∆ω'=I_n（Q_n+1-Q_n-1）-Q_n（I_n+1-I_n-1） （5-15）

用3个相邻的采样点来实现式（5-14），用I_n代替I（t），用Q_n代替Q（t），用（Q_n+1-Q_n-1）代替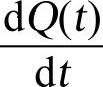，用（I_n+1-I_n-1）代替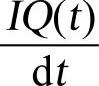，其中dt被忽略了。这是因为在数字系统中，dt是个固定的时间值，即是个常数，而我们需要的频差也只能是个相对值，因此计算结果的一个比例系数是不重要的。而这样还带来额外的好处是计算量减少了。

IIR滤波的具体特性可参考第3章相关内容。

本地载波的生成与第4章中的4.2.3节的部分是基本类似的，也是采用了查表法。唯一的区别是每个采样间隔内载波的相位增量不再是固定的值，而是在用接收频率计算的相位增量基础上用频差修正，即

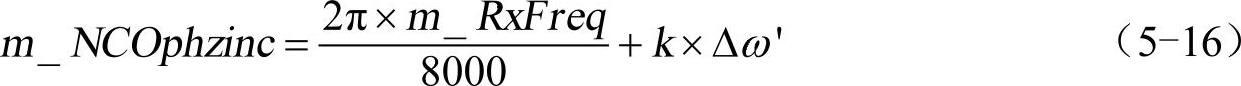
式中，m_RxFreq是接收频率；m_NCOphzinc是相邻采样之间的载波的相位增量；∆ω'是从式（5-15）计算得到并经过IIR滤波的频差估计；k是比例系数。k需要精心选择，这个参数太大了调整幅度就大，同步时间会短一些，会令本地载波在接收信号的载波附近波动过大，这个参数如果太小了，本地载波会比较接近接收信号的载波，但是同步过程会比较长。为此，这个系数在刚开始接收时采用一个较大的值（k=3×10^-6），令系统快速捕获，等接收了16个符号后，采用较小的系数（k=1.5×10^-6），令系统能稳定地跟踪接收信号的载波变化。