dsPIC实现调制器优化方案

调制器的相关参数如下：

●采样速率：8000样点/s。

●符号速率：31.25符号/s。

●载波频率：1500Hz。

●信号带宽：31Hz左右。

为了减少系统的运算量，脉冲成型、载波生成都采用了查表法来实现。调制器的整体框图如图4-9所示。

图4-9 调制器的dsPIC实现框图

因为系统的采样率是8000样点/s，所以在dsPIC系统上首先设计一个定时器，其周期是1/8000s，这样在每个定时中断内计算一次调制器的输出值。

1.脉冲成型

信号的采样率是8000样点/s，符号速率是31.25符号/s，因此每个符号周期内共有8000/31.25=256个采样点。脉冲成型表共有2048个采样点，即占用8个符号宽度。其代码如下：

为了便于理解系统的原理，把这个数据表用MATLAB画出图形来，其图形如图4-10所示。

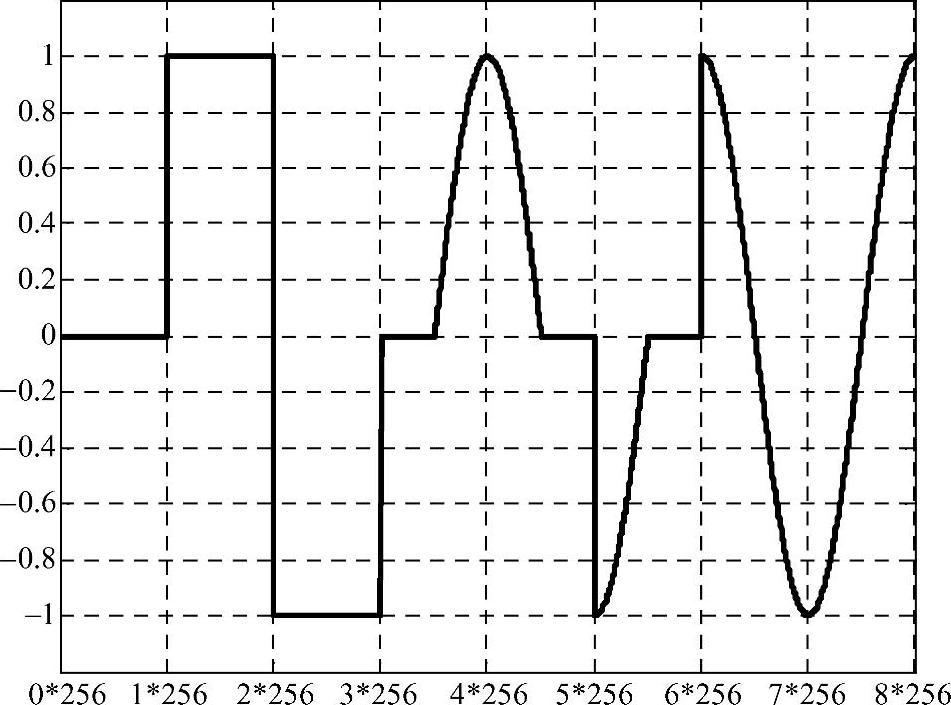
图4-10 调制器的脉冲成型表

为了便于分析，我们把上面的数据分为8组，如表4-3所示。

表4-3 波形成型表

系统每输入一个符号的信息（BPSK是1比特，QPSK是2比特），脉冲成型电路就输出上表中的某一段数据，共256个采样点。但是，要注意的是，上面的表中每段数据并不是正好对应着一个符号，而是对应了前一个符号的后半段和当前符号的前半段。

之所以要这样设计是基于两点考虑。其一是要在波形成型的同时完成差分编码；其二是因为这个数字调制器的波形成型是比较特殊的，当前的信号波形从时间上看虽然被限制在了一个符号周期内，但是其波形形状是跟前、后两个符号的形状相关的。

如果当前符号与前一符号的极性相同，则这个符号的前半周期是+1或-1，如果与前一符号的极性相反，则这个符号的前半周期是以0开始，以+1或-1结束的1/4周期的正弦波。当前符号的后半周期的情况是类似的，其形状是与后一符号的极性相关的。如果当前符号与后一符号的极性相同，则这个符号的后半周期是+1或-1，如果与后一符号的极性相反，则这个符号的后半周期是以+1或-1开始，以0结束的1/4周期的余弦波。

从图4-2b可以看出，调制系统共有4种可能的相位，但是调制器不是一直工作，即有数据要发送的时候才开始发送调制后的载波，如果没有数据要发送，就应该关闭载波的发送。这样做当然可以节约能源，但是更重要的是在时分双工系统中，由于收发双方共用一个载波频点，收发双方任何一个调制器如果始终发送信号，那么系统将无法完成双向通信。这样，除了上述的4种相位状态外，还应该加上一个0载波，或者无信号（载波关闭）状态。我们给这5个状态分别分配一个数字，如图4-11所示。

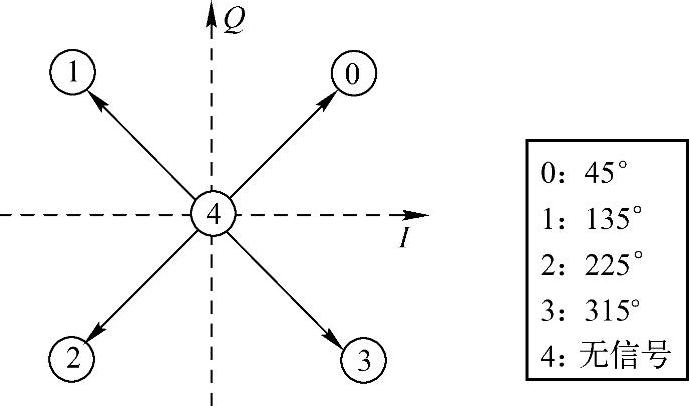
图4-11 绝对相位的对应关系

为了实现差分编码，我们要根据输入的信息比特计算出需要的相位变化值。相位变化状态可以有以下4种：相位不变（增加0°），增加90°，增加180°，减少90°。为了实现载波的关闭和打开，我们还需要再增加两个变化状态：载波关闭，载波打开。

我们用下面的数组来实现脉冲波形地址的生成。

上述的数组由6组数字组成，每组有5个整数，共30个整数。每组内数字的位置代表了前一符号的绝对相位。每个整数使用其低24比特。比特7～0表示当前符号的绝对相位，比特15～8表示Q支路信号波形在波形表中的序号，比特23～16表示I支路信号波形在波形表中的序号。

使用数组PSKPhaseLookupTable[6][5]就可以方便地实现QPSK的调制了。我们用一个例子来说明这个数组的使用。假设要被发送的一组二进制信息是：01110010。调制器的载波刚开始处于关闭状态，而且发送完毕后还需要把载波关闭。这样，整个调制过程说明如下。

这一组信息需要4个符号周期来发送出去，因为调制载波刚开始处于关闭状态，因此还需要两个额外的符号周期，发送之前需要一个符号周期把载波打开，发送结束后需要一个符号周期把载波关闭。对于发送前多出的一个符号，或可这样理解，因为是差分调制系统，需要一个额外的符号来给出最初的绝对相位，这样才能用载波相位差传递信息。下面我们分6步来说明整个调制过程。

1）因为载波关闭对应图4-11中的4号相位（无信号），第一个输入的符号是“载波打开”，所以选用数组PSKPhaseLookupTable中的PSKPhaseLookupTable[5][4]=0x330，用它来生成基带波形。这个数字告诉我们：当前绝对相位是图4-11中0号相位（45°），I、Q支路的波形都选用表4-3中的3号波形。

2）前一符号的绝对相位是图4-11中的0号相位（45°），输入的数字信息是01，根据表4-2，需要发送的符号是“增加90°”，所以选用数组PSKPhaseLookupTable中的PSKPhaseLookupTable[1][0]=0x611，用它来生成基带波形。这个数字告诉我们：当前绝对相位是图4-11中1号相位（135°），I、Q支路的波形分别选用表4-3中的6号和1号波形。(www.xing528.com)

3）前一符号的绝对相位是图4-11中的1号相位（135°），输入的数字信息是11，根据表4-2，需要发送的符号是“增加180°”，所以选用数组PSKPhaseLookupTable中的PSKPhaseLookupTable[2][1]=0x763，用它来生成基带波形。这个数字告诉我们：当前绝对相位是图4-11中的3号相位（315°），I、Q支路的波形分别选用表4-3中的7号和6号波形。

4）前一符号的绝对相位是图4-11中的3号相位（315°），输入的数字信息是00，根据表4-2，需要发送的符号是“相位不变”，所以选用数组PSKPhaseLookupTable中的PSKPhaseLookupTable[0][3]=0x123，用它来生成基带波形。这个数字告诉我们：当前绝对相位是图4-11中的3号相位（315°），I、Q支路的波形分别选用表4-3中的1号和2号波形。

5）前一符号的绝对相位是图4-11中的3号相位（315°），输入的数字信息是10，根据表4-2，需要发送的符号是“减少90°”，所以选用数组PSKPhaseLookupTable中的PSKPhaseLookupTable[3][3]=0x622，用它来生成基带波形。这个数字告诉我们：当前绝对相位是图4-11中的2号相位（225°），I、Q支路的波形分别选用表4-3中的6号和2号波形。

6）前一符号的绝对相位是图4-11中的2号相位（225°），需要发送的符号是“载波关闭”，所以选用数组PSKPhaseLookupTable中的PSKPhaseLookupTable[4][2]=0x554，用它来生成基带波形。这个数字告诉我们：当前绝对相位是图4-11中的4号相位（无信号），I、Q支路的波形都选用表4-3中的5号波形。

至此，这个调制过程就结束了。把这个过程用图4-12来表示。

图4-12 调制脉冲成型示例

需要再次说明的是，图4-12中，每一步的每个支路都要输出256个采样值，每一步占用的时间是1/31.25s，这样输出信号的采样率才能是8000样点/s。再联系到调制器的以1/8000s为周期的定时器，实际的操作就是每256个定时中断计算一次需要输出的符号，然后在下面的256个定时中断中，每次输出一个采样点数据。

2.载波产生

为了简化运算和提高计算速度，载波的生成也采用查表法。这个数据表的代码大致如下：

把这个表用MATLAB画出来，如图所示4-13。

图4-13 载波的生成数据

这些数据实际上是1/4周期正弦波的数据。这样是为了减少存储空间，因为一个正弦波的周期内的其他部分的形状与第一个1/4周期内的部分是基本一样的，在使用载波时，只要稍微用一点小技巧，就可得到一个周期内的几乎任何位置的数据。这个处理函数如下：

有了这个函数只要知道相位值（phase），就可以由此推算出载波的数值了。因为我们的数据表不可能是无限精细的，因此相位值只能是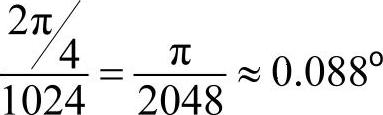的整数倍，即phase的取值范围是0～4095。这样的设计虽然没有实现绝对的准确，但是也能满足要求了。

之所以这样设计数据表，是因为调制器的载波频率很难与8000形成整数倍的关系，因此，每个采样点在一个载波周期内的位置不会是一个很完美的位置，相邻周期内，采样点的位置肯定也不相同。所以，数据表内的取样间隔只有尽量的密，才能保证精度要求。

下面说明一下如何计算每个采样点位置的载波相位。计算公式如下：

其中，是载波数据表内相邻采样值的相位差；TXPhase是当前载波在采样（采样间隔是1/8000s）点的相位；phase是整数，在使用函数Sine_lookup（int phase）之前，需要对4096取余数。

这样I、Q支路载波的计算代码如下：

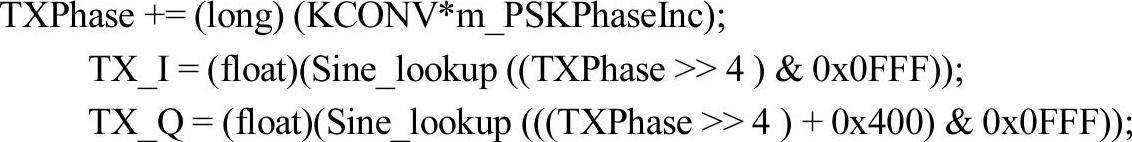
其中，m_PSKPhaseInc是载波在1/8000s的采样间隔内的相位增量。用下面的公式计算：

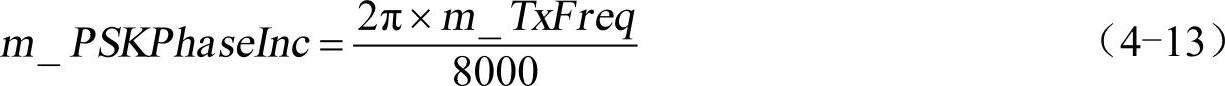
式中，m_TxFreq是载波频率。

代码中KCONV=651.8986469×16，也就是把真实的相位值扩大了16倍，在后面的代码中用右移4位来修正。这样做是为了提高精度，防止直接相乘取整后的四舍五入降低系统精度。

Q支路的相位值就直接在I支路的相位上增加了0x400，这其实正好对应着π4，即把余弦函数转换为正弦函数。

这样得到的TX_I和TX_Q就是载波的数值了，但是数值的取值范围不是一般的0～1之间，而是放大了32767倍，即0～32767。

下面只要在每个定时中断（定时间隔是1/8000s）中计算一下I、Q支路的载波与基带脉冲采样的对应点的乘积并相加就可以得到调制后的信号。不过这时的信号还是数字信号，通过一个D/A转换器件，就得到了真正的模拟的被调制到音频载波的QPSK调制信号了。