脉冲成型设计优化技巧

在上述的调制方案中，I、Q支路的脉冲成型是一样的，为了简化分析，我们将仅讨论一个支路。不失一般性，以I支路为例来分析。

I支路的信号可以表示为

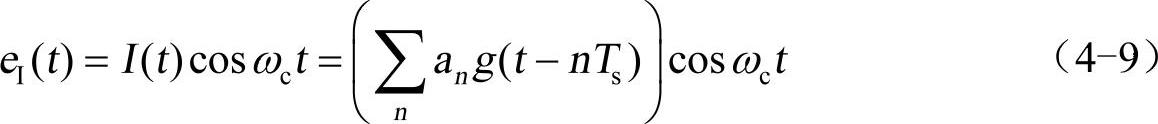
其中，a_n就是被调制的信息，为了简化分析，可以令其取值为+1或-1。g（t）是一段模拟信号，它与a_n、cosω_ct相乘，就完成了调制。g（t）的波形设计，就是这部分内容要重点讨论的脉冲成型问题。

脉冲成型设计，即g（t）的波形设计的基本要求就是要保证调制信息不能丢失。要满足这样的要求，把g（t）设计成矩形脉冲最简单了。这样脉冲成型设计的结果如图4-5所示。

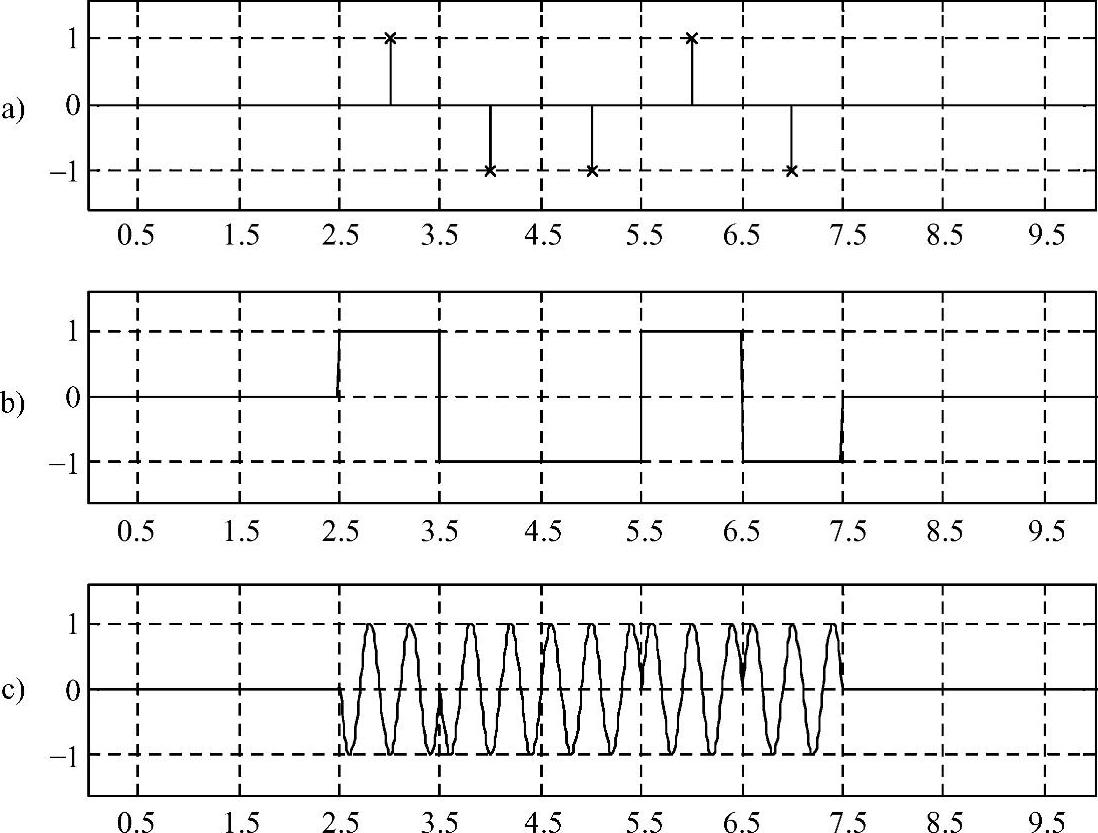
图4-5 矩形脉冲成型设计

a）数字信号波形 b）脉冲成型后的波形 c）调制后的波形

这样的设计存在一个严重的问题，就是在信号相位翻转的位置调制波形出现了不连续的跳变。比如横轴的3.5、5.5和6.5这些位置，就出现了急剧的跳变。这样的跳变带来的问题就是信号带宽的展宽，而展宽后的信号通过带限信道就会有频谱的损失，进而令解调后的基带波形出现严重的失真和码间串扰。

为了克服这个问题，奈奎斯特指出，只要把通信系统（包括发射机、信道和接收机）的整个响应设计成在接收端的每个采样时刻只对当前的符号有响应，而对其他符号的响应全为零，那么码间串扰的影响就能被完全抵消。

根据奈奎斯特准则，人们一般把脉冲成型滤波器设计成余弦滚降滤波器。余弦滚降滤波器的传递函数是

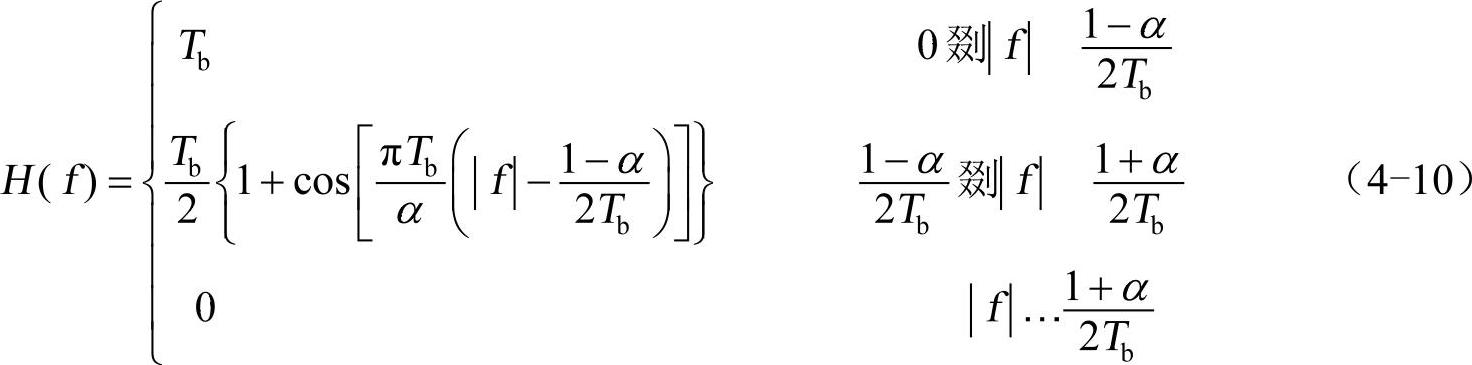
其中，α是滚降因子，取值范围是0～1；T_b是符号周期。与之相对应的滤波器的冲激响应是

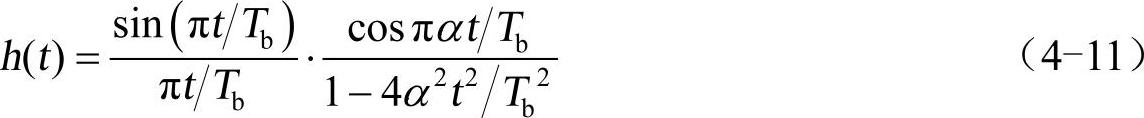
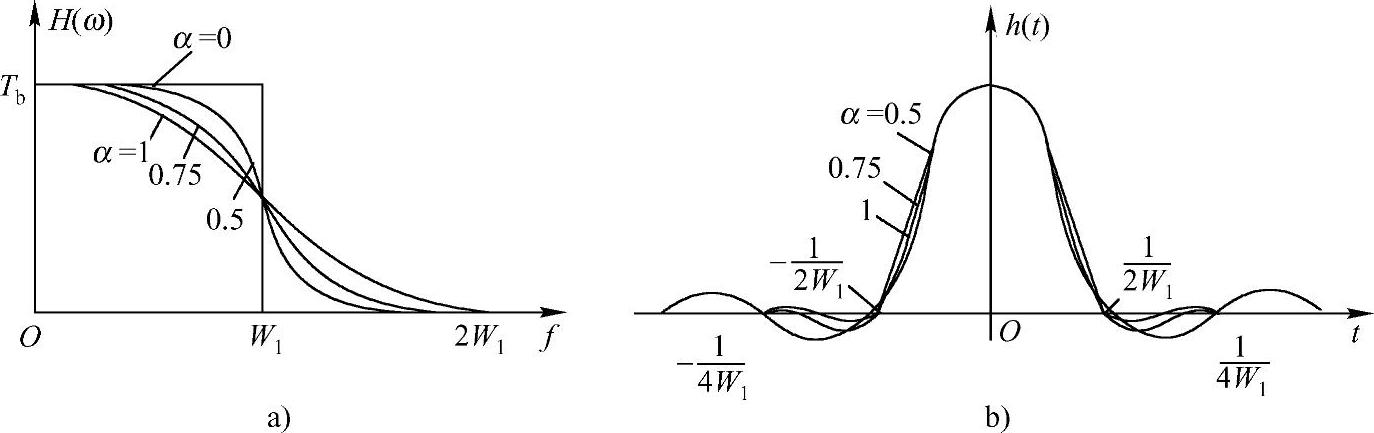
升余弦滚降系统如图4-6所示。其中，W₁为理想低通带宽。

(www.xing528.com)

图4-6 升余弦滚降系统

a）传输函数 b）冲激响应

我们再看这样的脉冲成型设计的波形如图4-7所示。

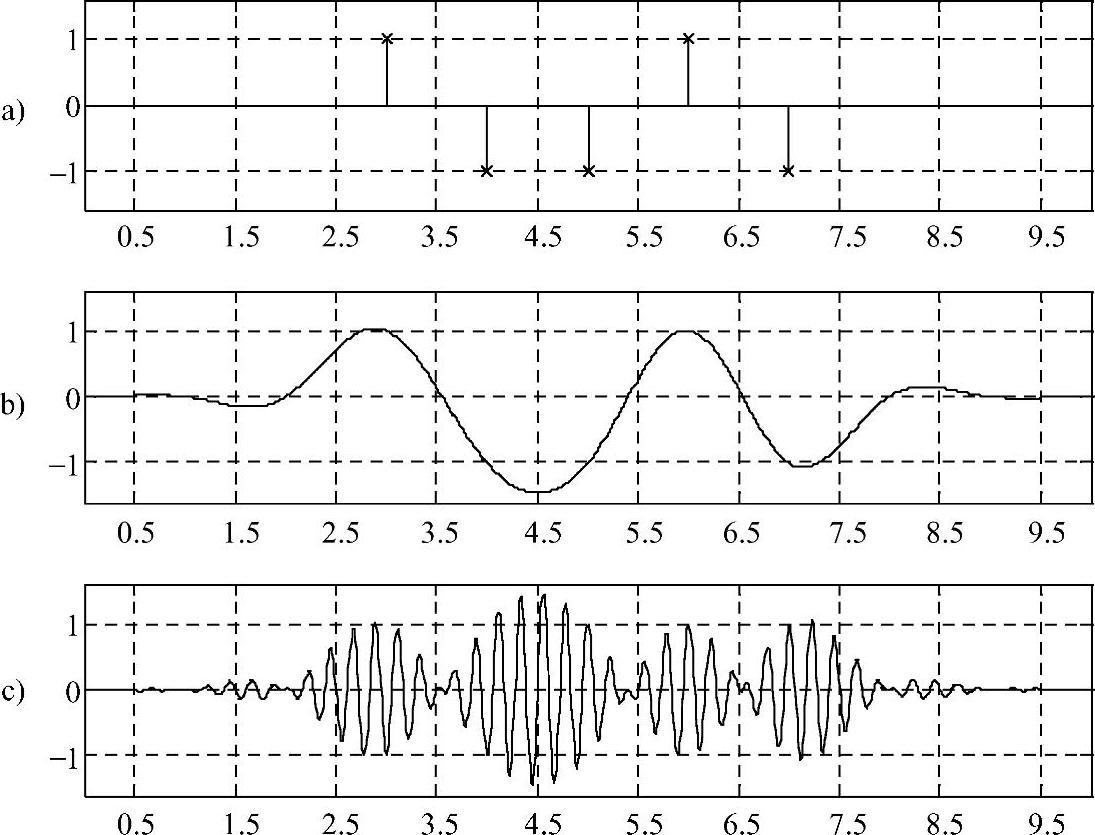
图4-7 奈奎斯特脉冲成型设计

a）数字信号波形 b）脉冲成型后的波形 c）调制后的波形

经过这样的设计，可以看出在信号相位翻转的位置，调制波形虽然相位不连续，但是由于载波在此处的幅度很小，使得不连续的跳变就非常不明显了。也就是说，这样设计的系统的带宽的确变窄了，经过带限信道不会对系统的频谱造成太大的损失。当然，这也可以从图4-6a中的传输函数看出来。

虽然其冲激响应理论上是无限长的，但是其他符号在当前符号的最大值点的贡献是0，因此没有码间串扰。但是，请大家注意，这样的无码间串扰是有条件的，即解调端的采样点必须严格地落在每个符号的中间。否则仍然会产生码间串扰。

为此，本节介绍的调制器所采用的脉冲成型设计采用了一种特殊的设计。其基本规则就是如果发送的数字信号是连1码或连0码，脉冲成型电路输出+1或-1，当前后码元不一样时，从前一码元的中间点开始到后一码元的中间点之间用正弦或余弦函数来过渡，其过渡点要为0，而且这当中只能单调下降或上升一次。采用这样的方式的脉冲成型设计如图4-8所示。

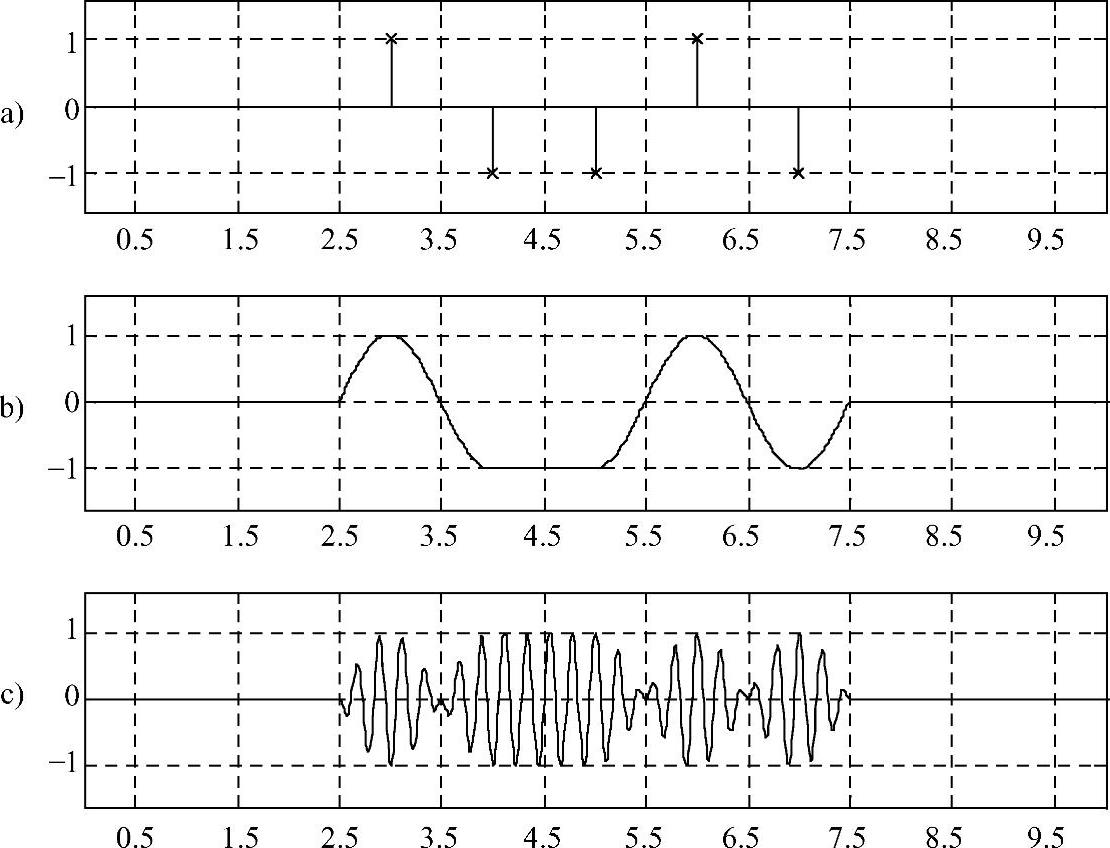
图4-8 正弦脉冲成型设计

a）数字信号波形 b）脉冲成型后的波形 c）调制后的波形

从图4-8可以看出，经过这样的设计，在信号相位翻转的位置调制波形虽然相位不连续，但是由于载波在此处的幅度很小，使得不连续的跳变就非常不明显了。这与奈奎斯特波形成型的结果是一样的。也就是说，这样设计的系统的带宽会很窄，经过带限信道后也就不会令系统的频谱造成太大的损失。接收端的基带波形失真也会小很多。

同时，这样的设计使一个符号的信号波形被限制在了一个符号周期之内，不会拓展到其他符号周期内，自然也就没有了码间串扰的问题。这样的设计还有一个额外的好处，就是接收端采样点不用像奈奎斯特成形方式那样，必须严格对准符号的中点。只要在符号周期内找一个信号比较大的点采样就可了。