MATLAB实现FIR滤波器

1.窗函数法

假设有一个截止频率为ω₀（rad/s）的理想数字低通滤波器，其表达式如下：

故其冲激响应序列h（n）为

这个滤波器是物理不可实现的，因为其冲激响应具有无限性和非因果性。为了产生有限区间长度的冲激响应，可以加窗函数将其截断。通过截断保留冲激响应的中心部分，就可以获得一个线性相位的FIR滤波器。例如，一个长度为51、截止频率ω₀为0.4rad/s的低通滤波器，用MATLAB实现如下：

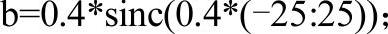
此处使用的窗是一个简单的矩形窗。根据帕塞瓦尔定理，这是在最小平方积分意义上，长度为61的滤波器中，对理想低通滤波器的最佳近似。下面的语句可画出该滤波器的频率响应：

其幅频响应如图3-13所示。

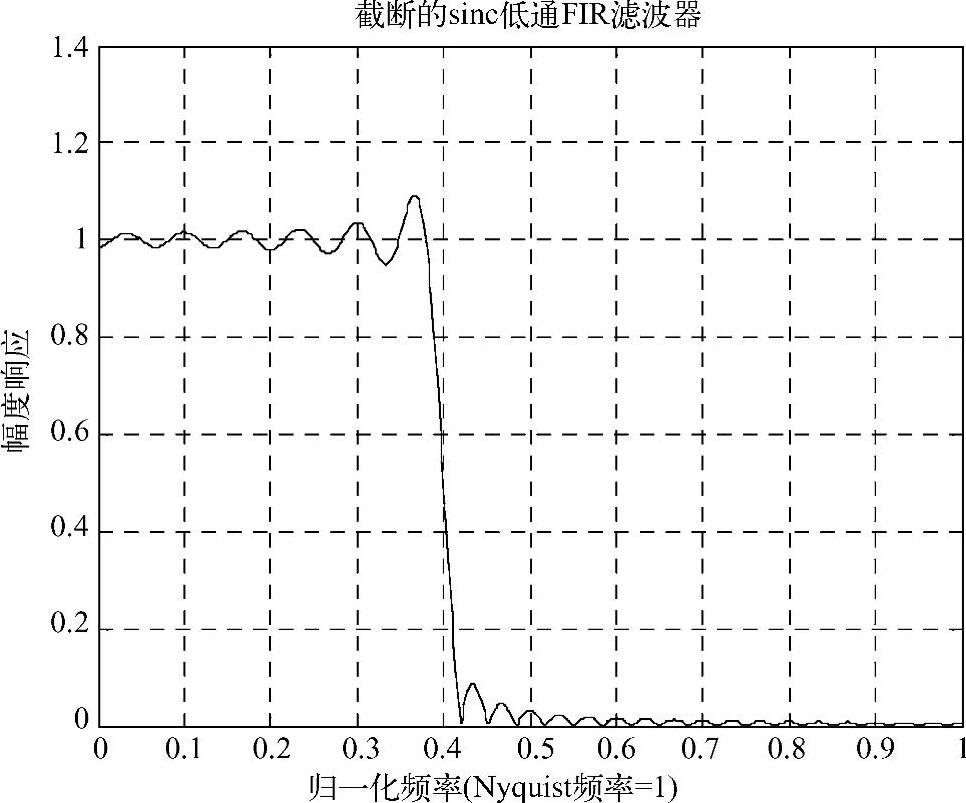
图3-13 截断的sinc低通FIR滤波器

通过图形可以看到响应中出现的波动，尤其是在通带和阻带的边缘，这就是所谓的“吉布斯”效应，通过滤波器长度的增加是不能够消除“吉布斯”效应的。但是若采用非矩形窗就可以减小“吉布斯”效应的幅度。通过在时域内乘以窗函数，就相当于在频域产生卷积或平滑的效果，以减小“吉布斯”效应的幅度。对前面的滤波器使用长度为61的汉明窗：

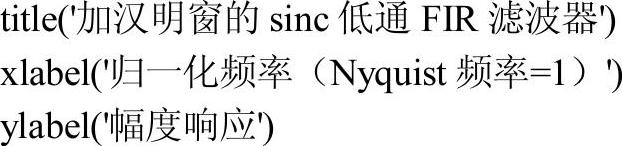
其幅频响应如图3-14所示。(www.xing528.com)

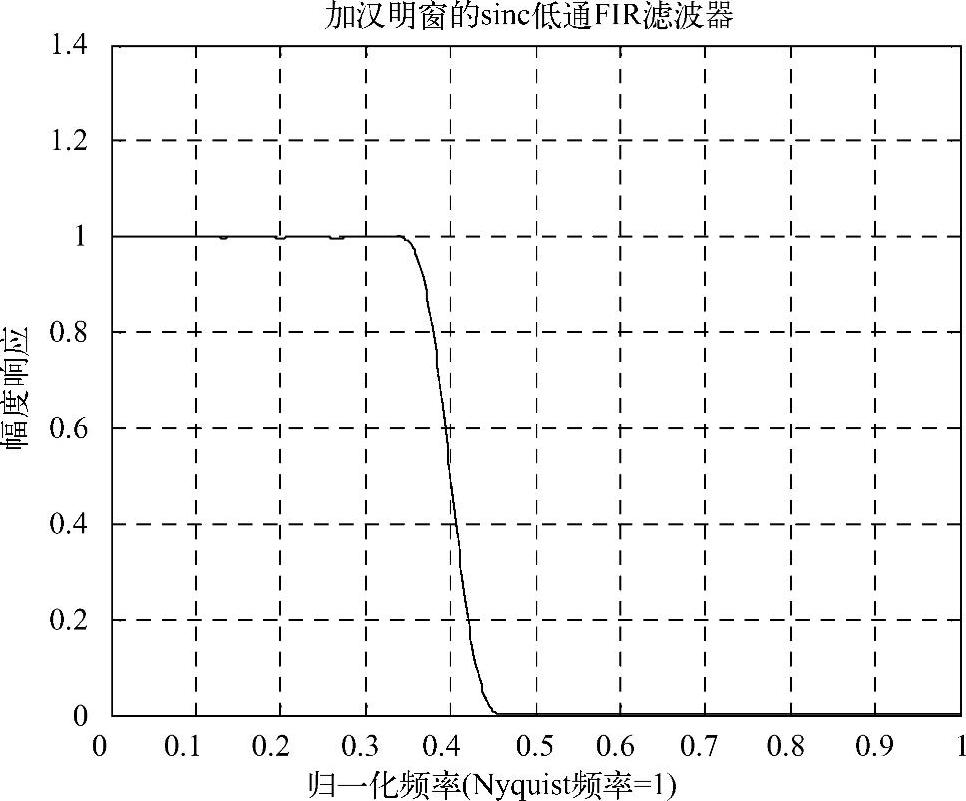
图3-14 加汉明窗的sinc低通FIR滤波器

正如我们所见，这大大减少了“吉布斯”效应的波动，但这种改善是以牺牲过渡带宽度和最优化为代价的（加了非矩形窗后，从通带到阻带的斜坡变长了，且不再是平方积分最小了）。

2.频率采样法

在加窗设计中，从理想滤波器的冲激响应序列着手，用截断法和加窗法就可得到所要求的滤波器频率响应。而根据频率采样法设计FIR滤波器时，则是从要求的滤波器频率响应出发，用内插法和离散傅里叶变换（DFT）获得滤波器的冲激响应。由此可看出，频率采样法可以拥有对任意频率响应波形滤波器的设计，具有多样性的特点，因此有很大的应用价值。

假设待设计的FIR滤波器的传输函数用H_d（e^jω）表示，对它在0～2π区间等间隔采样N点得到

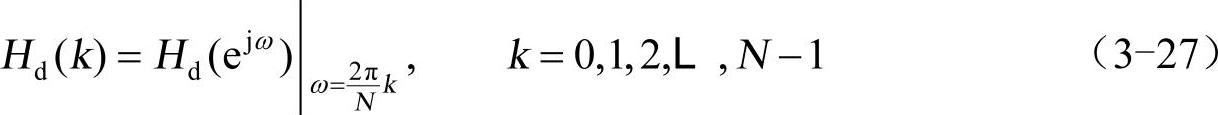
再对N点H_d（k）进行离散傅里叶逆变换（IDFT），得到h（n）

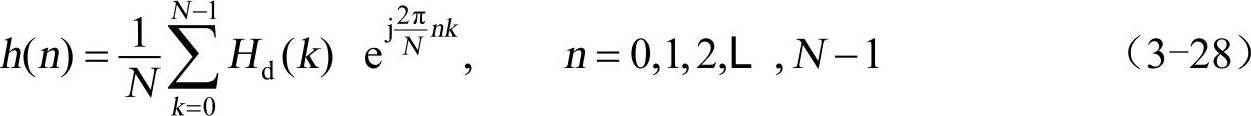
式中，h（n）作为所设计的滤波器的单位取样响应，其系统函数H（z）为

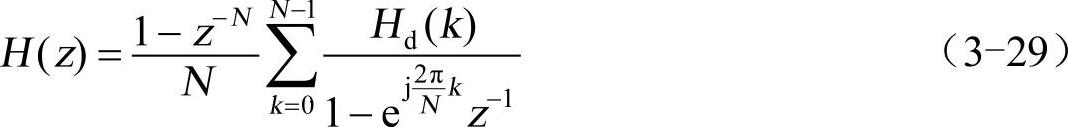
上式就是直接利用频率采样值H_d（k）形成滤波器的系统函数，上面两个式子都是应用频率采样法设计的滤波器，它们分别对应不同的网络结构。

频率采样法设计滤波器最大的优点是直接从频率域进行设计，比较直观，也适合设计具有任意幅度特性的滤波器。但边界频率不易控制，如果增加采样点数N，对确定边界频率有好处，但N加大会增加滤波器的成本，因此，它适合窄带滤波器的设计。

3.等波纹线性相位滤波器的设计

理想滤波器频率响应和实际滤波器频率响应之间的差值，也就是滤波器的逼近误差，在通带或阻带区间并不是均匀分布的，一般来说靠近边缘处误差较大，离开边缘处误差较小。因此将具有误差均匀分布特性的滤波器称为等波纹滤波器。由于它在通带和阻带上的误差是均匀分布的，故需要的多项式阶次比较低。而且对于线性相位FIR滤波器，可以导出一组约束条件，以实现最小化最大逼近误差，也可以是最大误差最小化或Chebyshev最佳逼近。