线性时不变系统的特点与应用

时域离散系统的作用是将输入序列转变为输出序列，系统的功能是将输入x（n）转变为所需输出y（n）的运算，记为

y（n）=T[x（n）] （3-2）

时域离散系统的作用如图3-1所示。

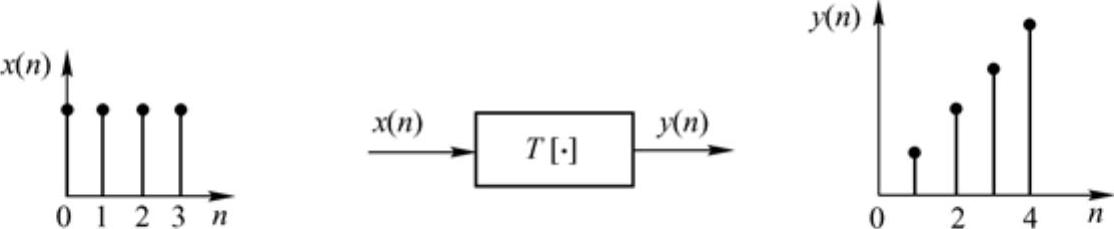
图3-1 时域离散系统的作用示意图

在时域离散系统中，最常用最重要的是线性时不变系统（简称LTI离散系统），很多物理过程都可用这类系统表征，且便于分析。

1.线性系统

满足叠加原理的系统称为线性系统。设x₁（n）和x₂（n）分别作为系统的输入序列，输出分别用y₁（n）和y₂（n）表示，即

y₁（n）=T[x₁（n）]

y₂（n）=T[x₂（n）]

那么，线性系统一定满足下面两个公式：

T[x₁（n）+x₂（n）]=y₁（n）+y₂（n）

T[ax₁（n）]=ay₁（n） （3-3）

满足第一个公式称为线性系统的可加性，满足第二个公式称为线性系统的比例性或齐次性，式中a是常数，将以上两个式子结合起来，可表示为

y（n）=T[ax₁（n）+bx₂（n）]=ay₁（n）+by₂（n） （3-4）

式中，a、b均是常数。

2.时不变系统(www.xing528.com)

如果系统对输入信号的运算关系T[⋅]在整个运算过程中不随时间变化，或者说系统对于输入信号的响应与信号加于系统时间无关，则这种系统称为时不变系统，用公式表示为

y（n）=T[x（n）]

y（n-n₀）=T[x（n-n₀）] （3-5）

式中，n₀为任意整数。检查一个系统是否是时不变系统，就是检查其是否满足上式。

3.线性时不变系统输入与输出之间的关系

设系统的输入x（n）=δ（n），系统的输出y（n）的初始状态为零，定义这种条件下系统输出称为系统的单位取样响应，用h（n）表示。即单位取样响应就是系统对于δ（n）的零状态响应。用公式表示为

h（n）=T[δ（n）] （3-6）

h（n）和模拟系统中的h（t）单位冲激响应类似，都代表系统的时域特征。

设系统的输入用x（n）表示，则将其表示成单位序列移位加权和为

那么系统的输出为

根据线性系统的叠加性质和时不变性质有

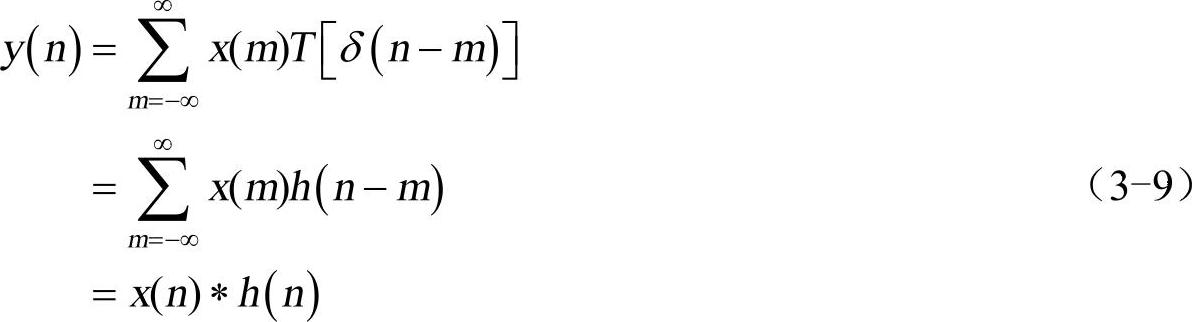
式中，符号“∗”代表卷积运算，即线性时不变系统的输出等于输入序列和该系统的单位取样响应的卷积。