空气冲击波参数的理论分析

2.4.3.1　条件假定

设有球形装药在无限均匀静止的空气介质中爆炸,且满足下列假定条件:

(1)炸药爆轰所释放的能量全部用于形成空气冲击波。

(2)相对空气冲击波所传距离和时间,炸药尺寸、爆轰所用时间及其向空气输入的质量均忽略不计。

(3)受扰动空气介质(即炸点至冲击波波阵面内的空气)满足理想气体绝热等熵流动,绝热指数保持不变。

(4)空气冲击波波阵面前方存在一个状态参量渐变区,但忽略其厚度和时间。

(5)空气冲击波波阵面上的介质状态满足C-J条件,即cm+um=Dm。

因此,可利用球对称散心爆轰研究结果研究空气冲击波参数。

2.4.3.2　空气冲击波压力

球面冲击波示意图如图2.14所示。根据球对称散心爆轰研究结果,可知空气冲击波于tR时刻传播至距炸点R处的初始压力,即峰值压力为

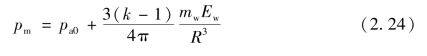
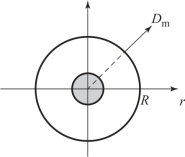
图2.14　球面冲击波示意图

式中,k为空气绝热指数;mw、Ew分别为炸药质量和单位质量爆炸所释放的能量;pa0为空气初始压力。

此时,波阵面后各处压力为

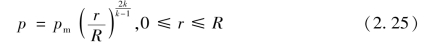
由式(2.25)可知,随着传播距离R的增加,空气冲击波峰值压力呈三次方关系衰减直至与空气初始压力相等,其内各处压力与距离r的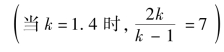次方呈正比。由式(2.25)还可知,对固定测压点即r一定时,当冲击波传播距离R<r时,该点压力为空气初始压力;当冲击波传播距离R=r时,该点压力突升为峰值压力;当冲击波传播距离R>r时,该点压力随R的增大而降低。由此得出的扰动空气的压力曲线与图2.9相同。当冲击波传播距离R和测压位置r满足一定条件时,可能出现p<p0即负压情形,但波阵面上不会出现负压。

2.4.3.3　空气冲击波正压区作用时间

在pm≫p0的前提下,有

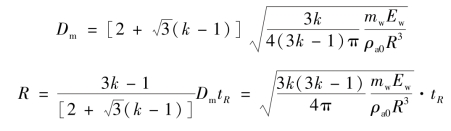(www.xing528.com)

式中,Dm为传播至R处时的冲击波波速;ρa0为空气初始密度。

由此可得空气冲击波传播至r处的时间为

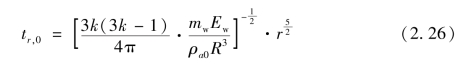
空气冲击波继续向前传播,该处压力不断下降直至与空气初始压力相等。记在tR时刻空气冲击波传播至距炸点R处时该处压力与空气初始压力相等,则由式(2.24)和式(2.25)可得

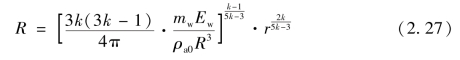
代入式(2.26),可得与此对应的时间即正压区结束时间,即

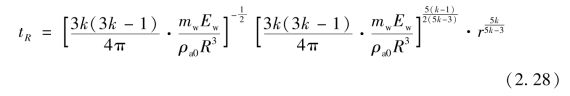
式(2.28)减去式(2.26)即为正压区持续时间,即

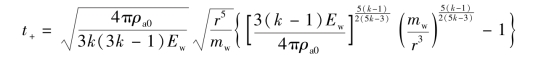
由此可得

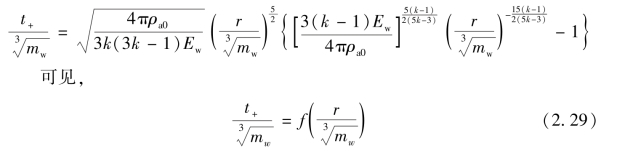
2.4.3.4　空气冲击波正压区作用比冲

同样在pm≫p0的前提下,有正压区比冲

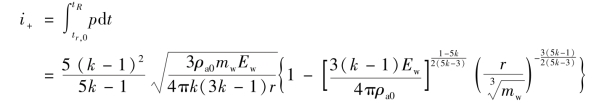
由此可得

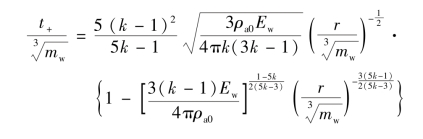
故有

上述理论分析均以pm≫p0为前提,亦即对比距离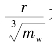不能过大。同样,由于接近炸点时爆轰产物对空气的作用比较复杂,有关假定未必合适,故上述有关公式要求对比距离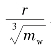不能过小。虽然适用范围受到局限,但对有关实验仍然具有一定的指导意义。