2.3.5.1 空气冲击波的形成
1.形成过程
为了便于理解冲击波的形成过程,我们以一维平面流动为例。爆轰波到达炸药与空气的分界面之前及其初始阶段的压力分布如图2.4所示。

图2.4 爆轰波到达介质时的压力分布
(a)爆轰波到达前;(b)爆轰波到达的初始阶段
图2.4中,p0为未经扰动时的空气压力;p为空气冲击波波阵面的压力;px为爆轰产物和压缩空气层界面处的压力;pH为爆轰波压力。
图2.4(a)表示炸药爆轰尚未结束。此时的介质分界面是指尚未受到爆轰波作用前的空气初始界面,即炸药端面的空气层。
图2.4(b)表示爆轰波到达空气初始界面后的初始阶段。此时,整个爆轰已经结束,爆轰波不复存在,初始爆轰产物最先与空气接触。由于初始爆轰产物的流速uj=D/4远大于一般空气中的声速(常温下约为340 m/s),因而以超声速方式强烈压缩空气(强扰动),必将在空气中形成初始空气冲击波,并以Ds的速度向前传播,波阵面处空气压力由p0上升为p;同时,空气形成稀疏波向爆轰产物中传播,使爆轰产物压力由pH下降,爆轰产物与空气的分界面以ux的速度向前运动,压力为px。
由于受冲击波扰动后的空气声速大于Ds,而爆轰产物后续的膨胀速度要小于最初的膨胀速度和受扰动空气介质的当地声速,所以,后续爆轰产物的膨胀不会产生新的空气冲击波(在受到空气反向压缩以前)。同时,随着空气冲击波传播距离的增大,消耗爆源能量增多,表现为冲击波传播速度Ds不断减小,直至衰减为未受扰动空气的声速,之后呈声波传播。需要注意的是,除了初始瞬间外,空气冲击波的波阵面不是空气与爆轰产物的分界面,波阵面前后都是空气,分界面前是空气、后是爆轰产物。
因此,空气冲击波的形成,直接原因是爆轰产物高压和高速流动产生的膨胀,根本原因是炸药爆炸能量在空气中的释放。
2.爆轰产物的膨胀
假设装药在无限空气介质中爆炸,在爆轰产物膨胀的最初阶段,压力下降很快。对中等威力的炸药,压力p≥pk≈200 MPa时,爆轰产物的膨胀规律近似为
![]()
或
![]()
式中,![]() 为爆轰产物的平均初始压力,按瞬时爆轰估算;V0为装药的初始体积;K表示某个中间状态,pK、VK为该状态时的爆轰产物的压力和体积。
为爆轰产物的平均初始压力,按瞬时爆轰估算;V0为装药的初始体积;K表示某个中间状态,pK、VK为该状态时的爆轰产物的压力和体积。
若装药为球形,则V∝r3或p∝r-9。假如爆轰产物的半径r膨胀到1.5 r0(r0为装药半径),那么,压力变化为

当爆轰产物膨胀至原半径的1.5倍时,则有

式中,![]() 。对中等威力炸药,有ρ0=1.60×103 kg/m3,D=7 000 m/s,则
。对中等威力炸药,有ρ0=1.60×103 kg/m3,D=7 000 m/s,则![]() MPa,故
MPa,故

可见,爆轰产物膨胀的最初阶段压力下降很快。在r≥1.5 r0以后,由于爆轰产物内的压力仍很高,它还将继续膨胀,一直到其运动惯性被空气介质阻力耗尽为止。通常把爆轰产物压力下降为p0时的体积称为爆轰产物的极限体积V1,可以用下面的方法粗略估算。由于爆轰产物的压力p<pK,爆轰产物的膨胀规律不能再用多方指数的等熵方程,而应采用理想气体绝热等熵方程:
![]()
式中,k为爆轰产物的绝热指数,一般取1.2~1.4。则

将![]() 代入式(2.4c)得
代入式(2.4c)得
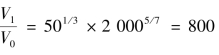 ,膨胀比
,膨胀比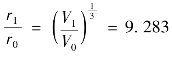 ;
;
当 ,膨胀比
,膨胀比 。
。
因此,对中等威力炸药,爆轰产物膨胀到p0时的极限体积约为原体积的800~1 600倍,此时爆轰产物的半径约为原来半径的10倍(球形装药)或30倍(柱形装药)。但是,爆轰产物最初膨胀到p0时并没有立即停止运动,由于惯性将继续运动,即继续膨胀(又称过度膨胀)。这种膨胀一直延续到惯性消失为止。这时,爆轰产物膨胀的体积达到最大(比极限体积大30%~40%),其平均压力低于未经扰动介质的压力p0。由于爆轰产物内部压力低于p0,就出现周围介质反过来对爆轰产物进行第一次压缩,使其压力不断回升。同样,惯性运动的结果,产生过度压缩,爆轰产物的压力又稍大于p0,并开始第二次膨胀和压缩的脉动过程。如此反复,直至爆轰产物的再次膨胀速度小于空气声速。
图2.5为球形装药爆炸后,某固定时刻在不同位置处测得的空气压力。中心为炸药爆炸前的位置,中间是爆轰产物,其外是空气介质,最外面为空气冲击波波阵面,其压力最大,又称峰值压力。波阵面后压缩区压力衰减很快,在压缩空气层的后面有一负压区(又称稀疏区),其压力低于未经扰动介质的压力p0。

图2.5 冲击波波阵面后压力分布示意图
如果我们在距炸心r处(注意:此r不是爆轰产物半径)进行压力测定,冲击波通过后可测得该点空气冲击波超压随时间变化的Δp(t)曲线。对1 kg梯恩梯(TNT)的爆炸,在5 m远处得到实验结果如图2.6所示。空气冲击波到达该点的瞬间,介质压力由p0突跃到p1,随后压力很快衰减,经过t+时间后压力低于未扰动介质的压力。通常把这种冲击波称为理想空气冲击波,其中AB经过t+时间后压力低于未扰动介质的压力。通常将AB段称为正压区,BC段称为负压区。对于带壳装药来说虽然空气冲击波曲线存在细节不同,但变化规律基本与无壳装药相同。
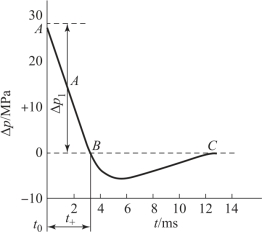
图2.6 1 kg梯恩梯爆炸后在5 m远处的Δp(t)曲线
3.炸药爆炸传给冲击波的能量
炸药爆炸时,传给空气冲击波的能量可以根据热力学的结果进行简单估算。爆轰产物膨胀到极限体积V1时所具有的内能E1为

炸药爆炸释放出的初始能量E为
![]()
式中,m为炸药的质量;Qv为单位质量炸药的爆热;ρ0为炸药密度;V0为爆炸前炸药的体积。
注意:式(2.5)隐含表示产物内部压力处处相等,这种前提将产生问题。
如果忽略爆轰产物剩余动能和其他能量损耗,则炸药爆炸传给冲击波的能量Es为
![]()
将式(2.5)和式(2.6)代入得
![]()
将式(2.6)代入式(2.7)可改写为
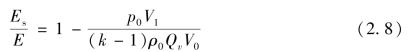
对中等威力的炸药,取Qv≈4 200 kJ/kg,ρ0=1.60×103 kg/m3,若![]() ,则代入式(2.8)可得
,则代入式(2.8)可得

若k=1.4时,则![]() 。
。
由上述估算可知,裸露装药爆炸时大约有90%以上的能量传给了冲击波,而留在爆轰产物中的能量不到10%。实际上传给冲击波的能量要少得多,这是由于爆轰产物膨胀过程的不稳定性和炸药爆炸时不能释放全部能量(以标准条件下的定容爆热衡量)所致。一般来说,传给冲击波的能量大约占炸药总能量的70%。在空气中进行核爆炸时,大约有50%的总能量是以空气冲击波形式传出的。
2.3.5.2 空气冲击波的传播
为简化起见,把弹丸装药看成球形装药,从中心起爆。如图2.7所示,弹丸爆炸后,炸药变为一团高温高压气体——爆轰产物。在爆轰波传至装药表面以前,空气不受扰动。装药全部爆轰完毕后,区域1内的爆轰产物开始向外膨胀,并压缩与之邻接的空气层。爆轰完成瞬间,爆轰产物外层的流动速度![]() (在γ=3、D=7 000 m/s时,高达1 750 m/s),远大于初始空气声速,故被压缩的空气层(区域2)在未被压缩的空气(区域3)中产生冲击波,形成一个介质状态突变的界面,这个突变界面即为空气冲击波波阵面。这时各区域内的压力分布见图2.8。
(在γ=3、D=7 000 m/s时,高达1 750 m/s),远大于初始空气声速,故被压缩的空气层(区域2)在未被压缩的空气(区域3)中产生冲击波,形成一个介质状态突变的界面,这个突变界面即为空气冲击波波阵面。这时各区域内的压力分布见图2.8。
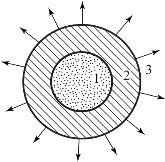
图2.7 空气冲击波产生示意图
1—爆轰产物区域;2—空气冲击波区域;3—未扰动的空气区域
图2.8(a)表示:在炸药爆轰完毕瞬间,爆轰产物初始压力极大,强烈压缩与其接触的空气,在空气中形成初始冲击波,使空气压力跃升一个超压Δp。图中Δp的宽度等于装药半径。

图2.8 爆轰产物的膨胀
图2.8(b)表示:空气冲击波波阵面脱离爆轰产物向前传播,空气冲击波波阵面不断地向已受扰动的空气(图中阴影部分)传入膨胀波。同时,空气稀疏波传入爆轰产物,使爆轰产物与空气分界面上的压力下降,表现为爆轰产物的膨胀。
图2.8(c)表示:爆轰产物继续膨胀,空气冲击波继续前传,爆轰产物与空气(已受扰动)分界面上的压力继续下降。
图2.8(d)表示:当爆轰产物分界面超压下降为0时(等于空气初始压力),由于惯性继续膨胀,直至惯性耗尽、停止膨胀。此时,爆轰产物外层一定区域内形成负压区,出现受扰动空气反向压缩爆轰产物。当这种压缩“过度”时,受扰动空气尾部也会出现一个负压区。
上述空气冲击波的形成和传播过程,还可以用图2.9表示。图中分别画出了在爆炸以后不同瞬间(t1,t2,…)冲击波的压力、位置与厚度,在t4时刻出现爆轰产物过度膨胀,t5时刻因过度膨胀出现负压区。

图2.9 空气冲击波的传播过程
对于某个确定位置(如固定目标)来说,它所遭受冲击波作用的超压-时间曲线Δp(t)如图2.6所示。由图2.6可见,冲击波波阵面在时刻t0到达此点,经历t+的时间称为正压作用时间。此阶段的压力冲量为
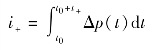
在中等距离上还存在负压阶段。当距离较大时,负压阶段不明显甚至消失。
2.3.5.3 空气冲击波在刚性壁面上的反射(https://www.xing528.com)
1.正反射
当空气冲击波遇到刚性壁面时,质点速度骤然降为零,壁面处质点不断聚集,使压力和密度增加,于是形成反射冲击波。平面定常冲击波在无限刚壁上的正反射如图2.10所示。

图2.10 平面定常冲击波在刚壁表面上的正反射
(a)入射波;(b)反射波
令Δp1=p1-p0,Δp2=p2-p0。
对入射波,有质量守恒方程
![]()
由于u0=0,故有ρ0 D1=ρ1(D1-u1),由此可得

由动量方程得
![]()
代入式(a)后得

由能量方程可得

整理后得


对反射波,有质量守恒方程
ρ1(-D2-u1)=ρ2(-D2-u2)
此处D2取负号,表示其运动方向与D1或u1相反。
由于u2=0,故有

由动量方程可得
p2-p1=(-ρ2D2)(u2-u1)=ρ2 D2 u1
代入式(d)得

由能量方程可得

比较式(b)式和式(e)可得

由式(c)可得

由式(f)可得

将式(h)及式(i)代入式(g),可得反射冲击波的峰值超压为
![]()
对空气来说,取绝热指数k=1.4,代入式(2.9)后得

由式(2.10)可知,对于弱冲击波,即Δp1≪p0时,有![]() ,这种情况与声波反射一致;对于很强的冲击波,即Δp1≫p0时,有
,这种情况与声波反射一致;对于很强的冲击波,即Δp1≫p0时,有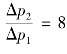 。
。
2.斜反射
当空气冲击波传播方向与障壁表面成φ0角时,就会发生冲击波的斜反射,如图2.11所示。

图2.11 空中爆炸时不同位置的p(t)曲线
1—入射波;2—正反射;3—正规反射;4—马赫反射
裸装药在空中爆炸时,不同位置空气冲击波超压变化情况如图2.11所示。空气冲击波通过B点时不发生反射,通过压电传感器测得一条典型的p(t)曲线如图2.11中1所示。地表面C、E、F、G、K各点与爆炸中心构成不同的入射角φ0,得到不同的p(t)曲线。对于C点,φ0=0°时,产生正反射,记录的p(t)曲线如图2.11中2所示,反射压力要比B点的高很多。E和F点由于入射波阵面的φ0<φ0c,只发生正规反射。其上面各点的反射压力与时间的关系如3所示。G和K点φ0>φ0c时,产生马赫反射波。马赫反射的p(t)曲线如4所示,反射压力比入射的更高。因此,装药在空中爆炸时,地表面不同位置处发生各种反射,而且使压力提高很多,这一点已为实验所证实。
空气冲击波反射后的压力与冲量计算如下:
正反射(φ0=0°)时:

式中,ΔpmG为爆炸时空气冲击波在地面的峰值超压,即入射波压力;p0为空气压力。
对于正规反射(0°<φ0≤φ0c),由实验可知,入射冲击波压力小于0.294 3 MPa时,反射波的压力与入射角无关,仍可用式(2.11)计算。
马赫反射(φ0c<φ0≤90°)时:
![]()
冲量的实验结果为

式中,i+G为地面爆炸时的冲量,N·s/m2。
爆炸高度对地面的反射波压力有显著的影响。从图2.11可以看到,爆炸高度对地面反射波压力产生双重影响。高度增加,离爆炸中心越远,入射波压力减小,但是又引起入射角的减小,反而使反射波压力增高。因此,要获得预定的反射波压力(如破坏目标所需压力),存在一个最有利的爆炸高度。即

式中,Hur为产生一定反射波压力Δp2时的最有利高度,m;Δp2为预定的反射波压力,MPa;m为装药质量,kg。
在最有利高度爆炸时,与产生Δp2所对应的水平距离为

2.3.5.4 空气冲击波的环流作用
冲击波在传播时遇到的目标往往是有限尺寸,这时除了有反射冲击波外,还发生冲击波的环流作用,又称绕流作用,如图2.12、图2.13所示。

图2.12 冲击波与障壁下反射的初始情况(用AUTODYN计算结果代替)
1—入射冲击波;2—反射冲击波

图2.13 冲击波绕过障壁物后的环流(用AUTODYN计算结果代替)
1—反射冲击波;2—入射冲击波;3—环流
假设平面冲击波垂直作用于一面很坚固的墙,这时就发生正反射,反射结果壁面压力增高为Δp2。与此同时,入射冲击波沿着墙顶部传播,显然,并不发生反射,其波阵面上压力为Δp1。由于Δp1<Δp2,因此稀疏波向高压区内传播。在稀疏波的作用下,壁面处空气向上运动,但在其运动过程中,由于受到墙顶部入射波后运动的空气影响而改变了运动方向,形成顺时针方向运动的旋风。旋风形成后,一方面使反射波后面的压力急剧下降,另一方面又和相邻的入射波一起作用,变成环流向前传播。
环流进一步发展,绕过墙顶部沿着墙后壁向下运动,这时墙后壁受到的压力逐渐增加,而墙的正面则由于稀疏波的作用,压力逐渐下降。即使如此,降低后的压力还要比墙后壁的大。环流波继续沿着墙后壁向下运动,经某一时刻到达地面,并从地面反射,使压力升高,这和空中爆炸时的冲击波从地面反射的情况相似。环流沿地面运动,大约在离墙后壁2倍墙高处的地面形成马赫反射,这时的冲击波压力大为增强。如果冲击波对高而不宽的障碍物(如烟囱等建筑物)作用,则在墙的两侧同时产生环流,当两个环流绕到墙后继续运动时就发生相互碰撞现象,碰撞区的压力骤然升高。高宽都不大的墙壁受到冲击波作用后,环流同时产生于墙的顶端和两侧。这时在墙后壁某处会出现三个环流波汇聚作用的合成区域,该区域压力很高。因此,在利用墙作防护时,必须注意到墙后某处冲击波的破坏作用可能比无墙时更加厉害。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




