Dirichlet 自由变形算法的优化方案

1.自由变形算法的基本原理

1986年，杨伯翰大学（Brigham Young University）的Sederberg和Parry提出了一种崭新的自由变形（Free From Deformation，FFD）算法。

变形在数学上可以看作一个由R³到R³的映射X=F（x），其定义域是待变形物体表面所包围的实体，其值域是变形后的实体。所以，关键问题是如何构造此映射，使模型的构造具有较好的直观性、交互性和透明性。

Sederberg和Parry使用了三变量张量积Bernstein多项式和一个控制框架来构造映射F（x），其算法如下：

1）在一个包围待变形物体的长方体中，构造局部坐标系O′-STU，如图11-21所示。

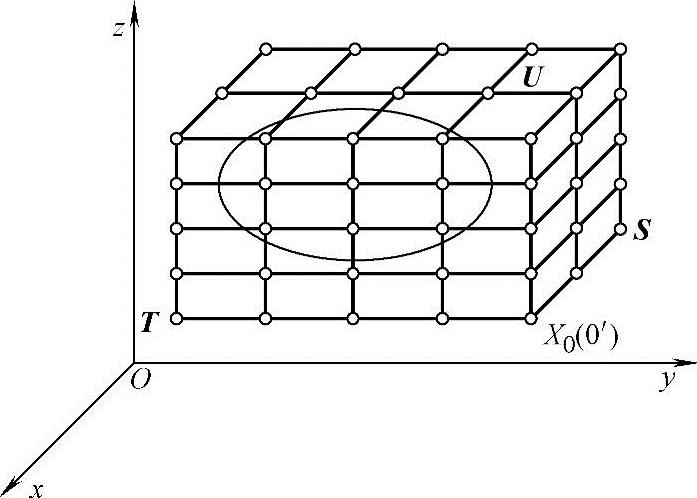
图11-21 构造局部坐标系和控制框架

图中，X₀（O′）是局部坐标系的原点；S、T、U是轴向量。笛卡儿坐标O-XYZ中任意一点X在局部坐标系中具有坐标（s，t，u）。

X=X₀+sS+tT+uU （11-17）

式中，X₀为局部坐标系的原点。

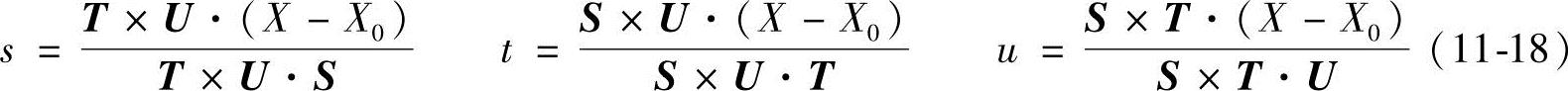
显然，对控制框架内的任意点，其局部坐标满足：0≤（s，t，u）≤1。

2）在长方体上构造控制顶点网格P_i，j，k，分别沿S、T和U三个方向用平行于O′TU、O′SU和O′ST坐标面的等距截面，将O′S、O′T和O′U等分为l、m和n个区间，则P_i，j，k可以表示为

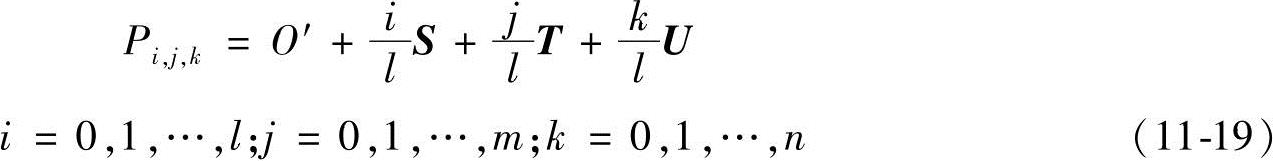
框架内任意一点的笛卡儿坐标X可表示为

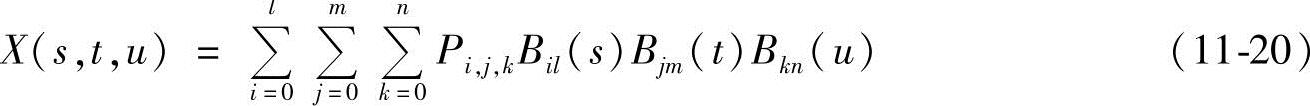
式中，B_il（s）、B_jm（t）和B_kn（u）分别为l、m和n次Bernstein多项式。

在建立了物体与框架的相互关系之后，用户可通过改变P_i，j，k的位置得到新的控制顶点P′_i，j，k和变形后的控制框架。若原控制框架的任一点X所对应的局部坐标为（s，t，u），则该点在框架变形后所对应的笛卡儿坐标X_ffd变形规则确定为

式（11-21）表明，由新的控制顶点计算变形后的物体时，应首先确定原控点框架内任意一点X所对应的局部坐标（s，t，u）。一般地说，此过程应根据原控制顶点和式（11-20）来解非线性方程组。在用Bernstein多项式来表示变形映射时，若原控制顶点满足式（11-19），则其局部坐标可用式（11-18）确定。

控制顶点P_i，j，k实际上就是Bernstein多项式的系数，与Bezier曲线、曲面一样，变形与控制顶点存在非常密切的关系。由于Bernstein多项式的性质，移动一个控制顶点将影响框架内的整个空间。因此，变形区域为框架内所有的点。实际上，变形只施加于框架内待变形物体上的点，即需要计算的仅是框架内变形物体上的点。当整个物体都位于框架内时，移动一个控制顶点将影响整个物体的形状。为使变形局部化，可采用较小的框架。当物体的一部分位于某个较小框架内时，将获得局部变形。此时框架与物体相交，为保持物体表面的连续性，框架与物体相交面上的框架顶点应保持不变，为保持切向向量或曲率连续，需对框架控制顶点的位置提出更严格的要求。因为物体的变形是由框架控制顶点的移动产生的，要求精确移动物体上的一个给定的点将是非常困难的，需要反复试验才能获得所期望的效果。

2.Dirichlet自由变形算法

FFD算法的优点是：可与任何实体造型系统一起使用；可对任何形式、任何幂次的曲面进行变形，可整体也可局部使用；可应用曲面或多边形模型；可估计体积变化的程度，并存在一类保持体积不变的变换；参数曲线、曲面经FFD变换后仍是曲线、曲面；可应用于大多数功能性曲面。

尽管FFD算法有许多优点，但是FFD算法仅用长方体作为框架，严重地束缚了FFD算法的应用范围。因此，研究人员相继提出了许多扩展自由变形算法，从不同的角度来继承FFD算法的优点，克服其缺点，扩展FFD算法的应用范围。

Coquillart提出的扩展FFD算法^[17]可以使用非长方体控制框架，从而扩展了可能产生的变形。Kalar等提出的有理FFD算法^[18]给每个控制顶点都附加了权值，用户可以通过移动控制顶点或者修改权值来控制变形，与FFD相比，权因子提供了另一个控制变形的自由度。FFD通过移动控制顶点使控制框架产生变形，从而使物体产生变形，是一种间接变形的方法，难以准确控制物体的形状。Hsu等提出的直接FFD算法^[19]，可以让用户直接操作物体上的点，而不是控制顶点，由物体上点的位置变化，再计算物体上其他点的变化。控制顶点是非均匀分布的，因此可以在变化较复杂的区域应用较多的控制顶点。以上各种改进的FFD算法都对FFD算法的功能进行了某种扩展，但是并没有在本质上有所突破。FFD用了长方体局部坐标系，因此控制框架也必须是长方体的，这显然与要变形物体的多样性相违背。

Dirichlet（狄里克斯）自由变形算法（DFFD）^[20]是Moccozet在1997年提出的，是FFD算法的各种改进算法中非常成功的一种，也是目前应用最广泛的一种算法。该算法抛弃了对控制框架拓扑结构的限制，采用更为一般的Sibson局部坐标系，从根本上克服了FFD算法的局限性，使用更灵活通用。Dirichlet自由变形算法首次结合计算几何知识（Delaunay三角划分和Voronoi图）来实现。本小节将结合这两个计算几何知识来详细介绍Dirichlet自由变形算法的思想及实现。

（1）Voronoi图的基本概念 设p₁、p₂是平面上两点，L是线段p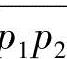的垂直平分线，L将平面分成L_L和L_R两部分，位于L_L内的点p_L具有特性：d（p_L，p₁）＜d（p_L，p₂），其中d（p_L，p_i）表示p_L与p_i（i=1，2）之间的欧几里得距离。这意味着，位于L_L内的点比平面上其他点更接近p₁，换句话说，L_L内的点比平面上其他点更接近于p₁的点的轨迹，记为V（p₁），如图11-22所示。如果用H（p₁，p₂）表示半平面L_L，而L_R=H（p₂，p₁），则有V（p₁）=H（p₁，p₂），V（p₂）=H（p₂，p₁）。

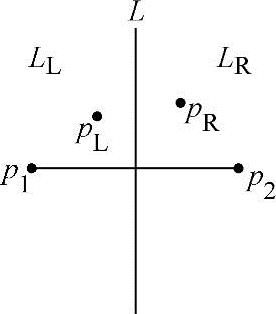
图11-22 V（p₁），V（p₂）的图示

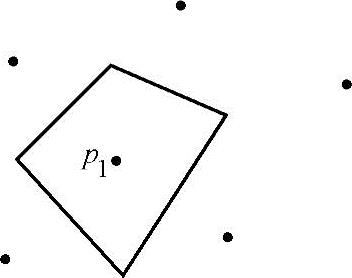
图11-23 n=6的一种V（p₁）

给定平面上的n个点的点集S，S={p₁，p₂，…，p_n}。定义V（p_i）=∩H（p_i，p_j），（i≠j），即V（p_i）表示比其他点更接近p_i的点的轨迹是n-1个半平面的交，它是一个不多于n-1条边的凸多边形域，称为关联于p_i的Voronoi多边形或关联于p_i的Voronoi域。图11-23中表示关联于p_i的Voronoi多边形，它是一个四边形，而n=6。

对于S中的每个点都可以做一个Voronoi多边形，这样的n个Voronoi多边形组成的图称为Voronoi图，记为Vor（S），如图11-24所示。该图中的顶点和边分别成为Voronoi顶点和Voronoi边。显然，|S|=n时，Vor（S）划分平面成n个多边形域，每个多边形域V（p_i）包含S中的一个点，而且只包含S中的一个点。Vor（S）的边是S中某点的垂直平分线上的一条线段或者半条直线，从而为该点所在的两个多边形域所共有。Vor（S）中有的多边形域是无界的。

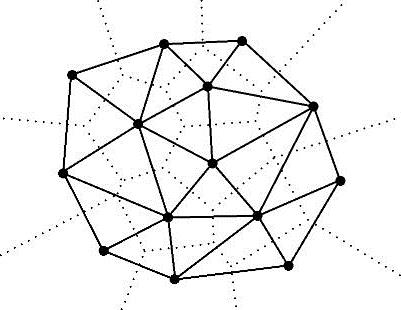
图11-24 Voronoi图及其对偶图

下面介绍几个重要Voronoi图的定理：

[定理11-1] 每个Voronoi点恰好是三条Voronoi边的交点，如图11-24所示。(www.xing528.com)

[定理11-2] 设v是Vor（S）的顶点，则圆C（v）内不含其他的点。

[定理11-3] Voronoi图的直线对偶图是S的一个三角剖分。

结论：点集S的最近意义下的Voronoi图，其Voronoi点的数目等于点集S三角剖分的三角形数目，而Voronoi多边形的数目等于点集S点的数目。如果点集S存在最远意义下的Voronoi图，那么Voronoi点的数目等于点集凸壳的三角剖分的三角形数目，而Voronoi多边形的数目等于凸壳顶点数目。在本节所述的算法的实现中，采用最近意义的Voronoi图，则其对偶图为网格点三角剖分的结果。因此，可以根据点集三角划分的结果来反过来求Voronoi图。

（2）Delaunay三角剖分 在Dirichlet自由变形算法中，需要应用到散乱点的Delaunay三角剖分算法。它是由俄国数学家Delauany于1934年提出的。可以用Delaunay三角剖分求其对偶Voronoi图，进而求Sibson坐标。所以Delaunay三角剖分是整个算法的基础，它的优劣将直接影响到整个算法的质量。本节将详细介绍本书所应用的三维数据点的Delaunay三角剖分算法。

Delaunay三角网格可以定义为：有公共边的Voronoi多边形称为相邻的Voronoi多边形，连接所有相邻的Voronoi多边形的生长中心所形成的三角网格称为Delaunay三角网格。

由图11-24可以知道，无论是最近意义下的Voronoi图，还是最远意义下的Voronoi图，都与点集的三角剖分有着密切的关系。最近意义下Voronoi图的对偶图就是点集的一种三角剖分，因而由点集的三角剖分可以计算Voronoi图；最远意义下Voronoi图的对偶图是点集凸壳（凸多边形）的一种三角剖分，由点集凸壳三角剖分不仅仅是构造Voronoi图的准备工作，而且它本身有许多应用。在本书的应用中采用前者，首先对点集进行三角剖分，然后由三角剖分的结果再生成Voronoi图。

Delaunay三角网格的外边界是一个凸多边形，它由节点集中的凸集形成，通常称为凸壳。它具有以下两个非常重要的性质：

1）空外接圆性质：在由点集S所形成的Delaunay三角网格中，其每个三角形的外接圆均不包含点集S中的其他任意点。扩展到三维空间，每个四面体的外接球体均不包含点集S中的其他任意点。

2）最大最小角准则：在由点集S所能形成的三角网格中，Delaunay三角网格中三角形的最小角度是最大的，即对任意相邻的两个三角形所构成的四边形来说，三角剖分要求该四边形的一条对角线所分成的两个三角形的六个内角中的最小值将大于另外一条对角线所构成的两个三角形的六个内角中的最小值，此准则使得三角剖分尽可能避免产生那种狭长的、具有尖锐内角的病态三角形。但是到了三维（及更高维）空间，最大最小角准则不再成立，这时会生成拓扑质量非常差的Sliver单元，即体积相当薄的单元。

无论是在理论上还是在应用上，平面凸域内散乱数据点的Delaunay三角剖分算法都已非常成熟，不少学者对此作出了贡献：Sibson从Delaunay三角剖分定义出发，提出了依据Thiessen区域准则进行优化的三角剖分方法^[21]；Cline与Renka等提出的方法^[22]是：首先对散乱数据点进行排序，再依次对散乱数据点进行三角剖分处理，以最小内角最大准则进行优化。对散乱数据点实行预排序，可大大缩短三角剖分的时间。Lawson和Cline-Renka三角剖分方法在具体算法及数据结构上不尽相同，但它们的运行效率都比较高，故获得了广泛的应用。

二维空间的Delaunay三角剖分算法有很多种，但是扩展到三维空间，相应的算法和研究文献比较少。本书采用广泛应用的Bowyer-Watson算法^[23]，它可以应用于多维空间。Bow-yer-Watson算法是通过顺序添加点到已经存在的Delaunay三角剖分来实现的，通常它从一个简单的包括将要进行剖分的所有点的超三角形开始。其算法实现如下：

步骤1：加入一个新的节点，找出所有外接圆包含新加入节点的三角形（见图11-25），并将这些三角形删除，形成一个空腔。

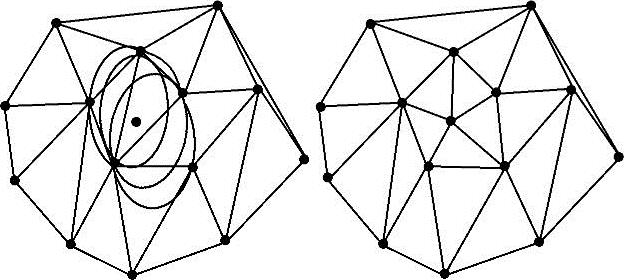
图11-25 Bowyer-Watson算法

步骤2：将空腔的节点与新加入的节点连接，形成新的Delaunay三角网格，如图11-25所示。

步骤3：调整数据结构，用新生成的三角形的数据填充被删除三角形的数据，余者添加在数组的尾部。

步骤4：返回步骤1，直至所有的节点都加入为止。

（3）Sibson局部坐标 DFFD算法中，待变形物体表面上的点只受其Sibson邻居的控制点控制，所以在三维的Sibson局部坐标系下，假设P为控制点集合，并记V（P）是P的Voronoi图，p是点集P的凸壳中的一点，P′=PU{p}，V（P′）是P′的Voronoi图。

设P的子集P_n={p_i|i=0，1，2，…，n，且p_i∈P′}，P_n称为p相对于P的Sibson邻居（自然邻居）集合，又记P_n′=P_nU{p}。

由于Sibson坐标既反映了空间点的Sibson邻居与该点之间的空间位置关系，也反映了Sibson邻居之间的空间位置关系，具有良好的空间插值特性。因此，把Sibson坐标作为Sib-son邻居对点p的运动影响系数，用（U₀，U₁，…，U_n）表示Sibson坐标。根据P_n和P_n′，n+1维向量U=（U₀，U₁，…，U_n）可唯一地确定物体表面上的点p，由p₀，p₁，…，p_n的线形组合可得

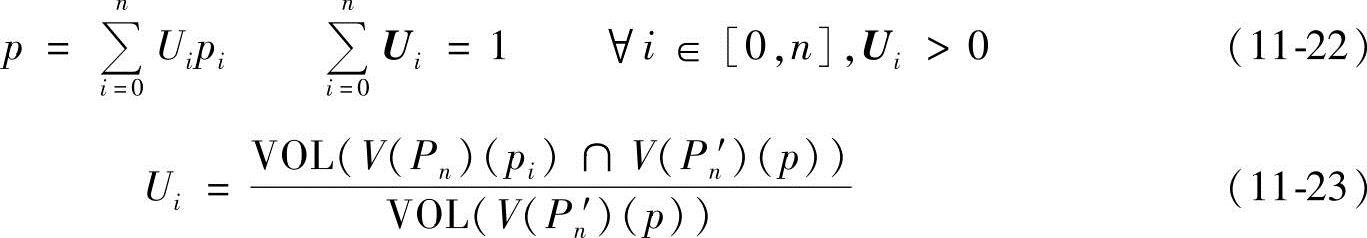
式中，VOL（）为返回给定Voronoi元的体积；V（P）（p）表示在Voronoi图V（P）中点p所在的Voronoi元。向量U_i是构造点p的Sibson坐标。当移动控制点时，物体上的点p也会发生位移，使物体产生变形。发生变形后，p点的新的空间位置由DFFD算法计算，得

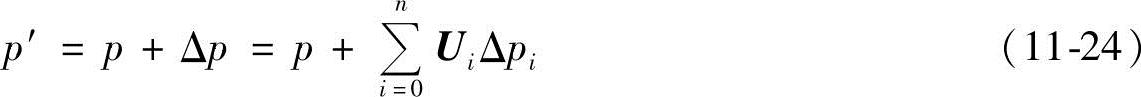
式中，p和p′分别是点p在变形前后的空间位置；Δp和Δp_i分别是点p及其Sibson邻居p_i的位移，Δp_i可等于0。

下面以二维的情况为例来说明如何计算点的Sibson局部坐标。图11-26是点集P={p₁，p₂，p₃，p₄}的Voronoi图，p是点集P的凸包内任意一点；图11-27是加入点p后的Voronoi单元，由于p₁、p₂、p₃、p₄所在的Voronoi单元都与p所在的Voronoi单元相邻，所以它们都是Sibson的邻居；图11-28是图11-26和图11-27的叠加，表示加入点p之后Voronoi图的变化，阴影部分为p₂对点p所在的Voronoi单元的贡献，该贡献在点p所在Voronoi单元中的比例就是p₂相对于点p的Sibson局部坐标值。

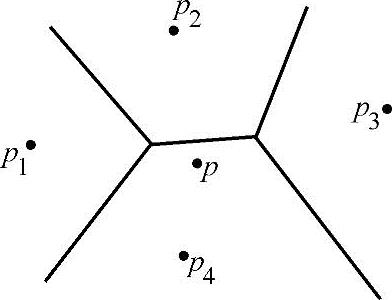
图11-26 由p₁～p₄生成的Voronoi图

图11-27 由p、p₁～p₄生成的Voronoi图

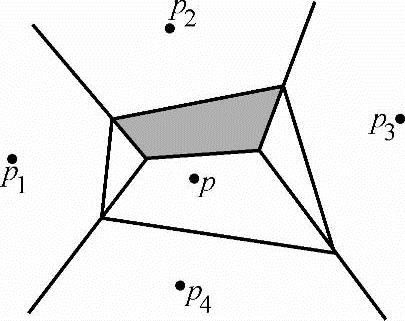
图11-28 点p₂对点p的Voronoi图做的贡献

（4）使用DFFD算法对物体进行变形的基本步骤

1）设计控制点集合。控制点集合是一些点的集合，不需要在控制点的集合上定义特殊拓扑结构。控制点可以在待变物体的表面上，也可以在待变物体的内部，但是物体需要变形的部分必须在控制点集合的凸包内。

2）计算控制点的Sibson局部坐标。针对物体上的每个点确定其Sibson邻居集合，利用式（11-22）和式（11-23）计算其Sibson局部坐标值。

3）对物体进行变形。移动控制点，可以使用任意方法移动一个或一组控制点，可见有多种实现途径。然后根据式（11-24）可以计算出物体上点变化的位移和新位置，从而得到物体变形结果。