纹理映射技术在三维人脸模型中的应用

1.纹理拼接图的产生

在计算机图像合成、计算机视觉以及三维人脸模型中，需要将多视角图像拼接融合后的静态纹理图像映射到三维模型上，生成栩栩如生的三维实体。由于设备的机械限制，广角的场景需要不同角度的成像进行平滑无缝的拼接融合，从显微镜、望远镜、手提摄像机到卫星成像系统也都需要图像融合技术来构造一幅图片所不能表现的全景图。对于这些图像的拼接融合，目前普遍的研究方法是通过两幅图像间的匹配特征点估计图像间的点变换关系，然后分别通过对两幅图像重采样注册到一幅更大的空白图像中形成合成图像，并在注册的过程中对两幅图像的交接边界处进行颜色平滑过渡，最后形成一张采样融合的包含两幅图像信息的图像。

整个算法主要包含三步：特征点的提取和匹配；图像间点变换的估计；交接边界处的颜色无缝过渡。对每步算法的研究虽然取得了一些成果，但还没有形成一种稳健的完全自动的拼接融合技术。Richard Szeliski以手动确定不少于4对特征点^[8]，并以特征点像素的亮度误差构造优化函数来估计图像间的点变换关系，取得了比较好的平面和深度场景融合效果，但此算法以亮度误差来做点变换估计，这对图像的光照变化非常敏感，而且整个算法的自动化程度不够。Pollefey详细研究了特征点自动提取和匹配问题^[9]，但没有针对图像处理做更深入的研究。Peter J分别运用多分辨率样条技术和单调函数插值技术对图像的交接处进行了有效的颜色平滑过渡^[10]，不过这是在特征点匹配和点变换的准确估计基础上完成的。

纹理映射能赋予三维人脸模型以真实感。由于采用的人脸模型是360°整体头部模型，所以需要可以构成环视效果的头部纹理图片与之对应。这就要先对正面图像和侧面图像进行无缝拼接，生成视点无关纹理图。输入的是三幅图像，需经过组合才能得到高分辨率的纹理拼接图。由于正向视图能提供高精度的脸部特征，所以要求正向视图保持不变，对侧向视图，首先沿预定义的脸部变形特征线进行变形，由于眼睛是人脸视图的关键，我们沿眼角裁剪图像，并加以拼接，沿眼角点垂线裁剪图像，并与正视图的对应左右眼角点垂线相互拼接。在侧面图像中定义了对应的脸部变形特征线。图11-12中，图a是正向视图中眼角及沿眼角点垂线的示意，图b、c给出了裁剪线在侧向视图中的对应位置。

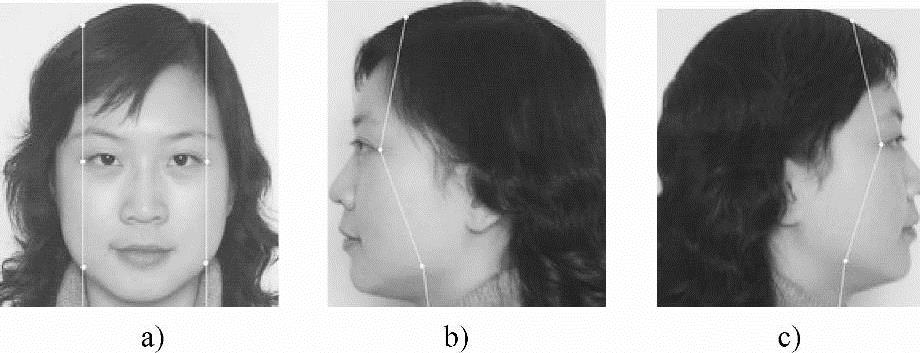
图11-12 不同方向视图的特征线对应关系

a）正向视图 b）左侧视图 c）右侧视图

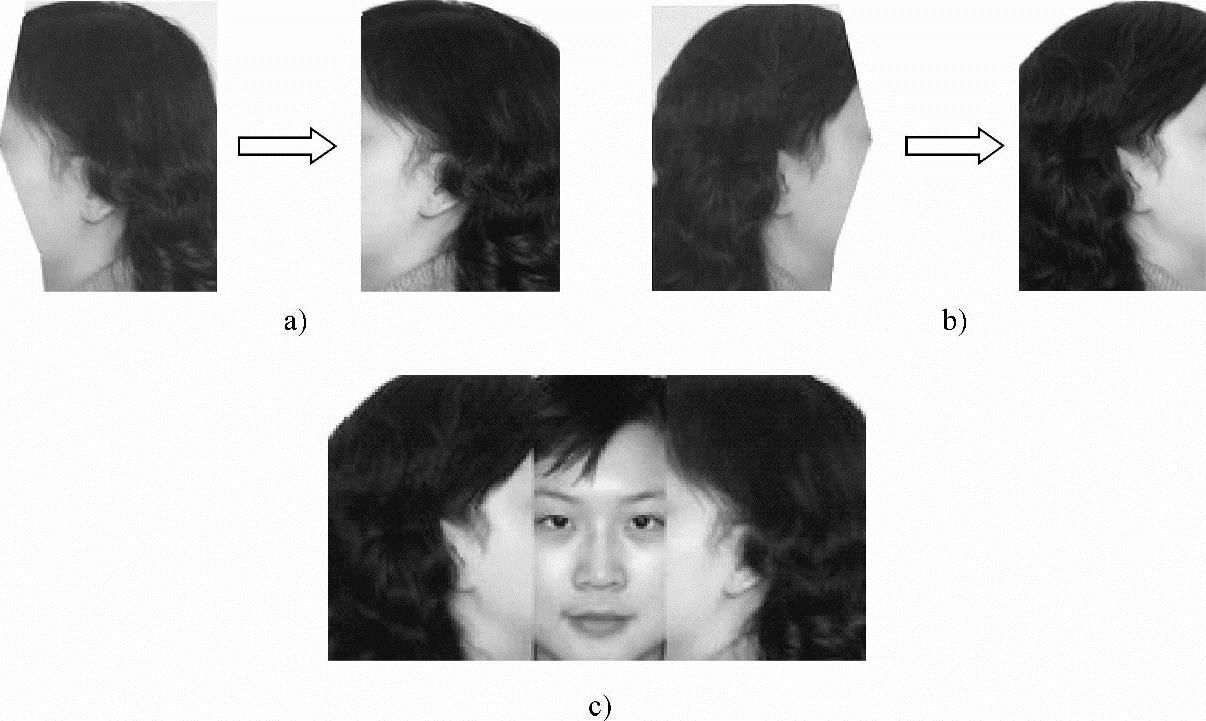
对侧面图像进行变形的准则是，将侧向视图中定义的变形特征线变换到正视图中对应变形特征线的位置，即沿左右图像的每一条扫描线作横向压缩或拉伸，使其变形后的脸部变形特征线与正向视图中的脸部变形特征线相重合。因此需对脸部变形特征线的两侧的图像像素进行重采样变换。左右视图的变形准则是将侧向视图中定义的变形特征线变换到正视图中对应变形特征线的位置，即沿左右图像的每一条扫描线作横向压缩或拉伸。图11-13是侧向视图的变换示意及初步得到的纹理拼接图。

正侧视图都只在一定视角范围内给出较好的人脸纹理。由于正面和侧面图像的光照条件和拍摄角度不同，简单的拼接会使皮肤颜色在拼接边界的变化很大，出现裂缝，如图11-13c所示。为了消除裂缝，一般采用多分辨率样条技术，实现图像之间的光滑拼接，该方法又叫图像金字塔法。图像金字塔可以看作代表原始图像的不同分辨率的一组图像的集合，高层的图像来自底层图像，底层的图像就是原始图像。高斯金字塔的第n层通过低通滤波和缩小，从第n-1层中产生，拉普拉斯金字塔的第n层是把高斯金字塔的第n+1层扩大，再和高斯金字塔的第n层求差得到。递归建立高斯和拉氏金字塔后，在返回过程中，求和重建图像得到了无缝拼接的图像。这里对分段特征线执行分段线性变换。而使用更高阶的特征曲线能对侧向视图执行更光滑的变形。最后遵循上面的图像变形规则，进而用多分辨率样条技术进行光滑，形成一张较大的无缝的纹理拼接图，正确给出特定人脸网格顶点的纹理坐标，如图11-14所示。

(www.xing528.com)

图11-13 侧向视图的变换及初步纹理拼接图的产生

a）左侧视图变换 b）右侧视图变换 c）纹理拼接图

图11-14 经光滑处理的最终纹理拼接图

2.纹理坐标

计算纹理坐标时，将每一个网格顶点（x，y，z）在正面、右侧、左侧图像上投影，记投影点位置分别为（x_f，y_f）、（z_r，y_r）、（z_l，y_l）。正视图中左右眼角点的x坐标分别为f₁、f₂，右侧图中的后脑勺边界和右眼角的x坐标分别为r₁、r₂，左侧面图中的左眼角和后脑勺边界的x坐标分别为l₁、l₂，并且记正面、右侧图像在纹理拼接图中裁剪的宽度分别为w₁、w₂。我们容易计算网格顶点在未实施图像变形前在纹理拼接图中的纹理坐标，具体是

然后遵循图像的变形特征线的变形，计算出网格顶点在变形纹理图像上的纹理坐标。程序中使用二维数组来定义纹理坐标textures[225][2]，其类型为GLfloat。由于绘制网格模型时选择了三角形，在进行纹理贴图时，使用glTexCoord2f（）函数把纹理图中的坐标映射到对应的三角形顶点的坐标。实验结果表明，纹理映射的结果比较理想。