从标准人脸模型到特定人脸模型的变换方法

1.特征点的变换

（1）全局变换 三维人脸模型上的任意一点P（X，Y，Z）以无穷小的欧拉角向其目标点P′（X′，Y′，Z′）作刚性运动，可以描述为

式中，θ_X、θ_Y和θ_Z是围绕X、Y和Z轴的旋转角度；S_X、S_Y和S_Z分别是比例因子；（T_X，T_Y，T_Z）^T是平移向量。全局变换可以等价地看成是对这9个刚性运动参数的估计。进行垂直影射后，可以通过计算三维人脸模型到二维人脸中心的距离来得到平移向量。让P_l、P_r、P_c、P_m分别代表左眼中心点、右眼中心点、两眼的中点以及嘴部的中心点，P_l′、P_r′、P′_c、P_m′是三维人脸模型中二维投影的相关特征。对比例因子S_X和S_Y进行了如下的定义：S_X=||P_l-P_r||/||P_l′-P_r′||，S_Y=||P_c-P_m||/||P_c′-P′_m||。在平面帧中，脸的深度是不可见的，为了确保自动性，S_Z将应用线性膨胀性取S_X和S_Y的平均值。头部的倾斜角度θ_Z可以通过测量线段P_lP_r和二维水平轴之间的夹角获得。θ_Y可以应用基于横截面的方法来获得。至于θ_X，由于缺少深度信息，所以我们假设头部与X轴是平行的，即θ_X=0。

（2）局部变换 4个脸部特征，如本系统中的眉毛、下巴、眼睛和嘴，将分别得到变换，如图11-3所示。8个眉毛节点（黑色圆点）用来代替提取出的8个眉毛特征点。在下巴替换中，三维人脸模型的5个下巴节点（黑色圆点）通过伸缩运动与提取出的二维下巴轮廓相吻合。通过对人体测量学和肌肉运动的研究，中间的三个圆点是与上面的两个方形节点相连的，而另外两个圆点也和对角的方形节点相连。嘴部变换包括仿射转换（Affine Transformation）和轮廓转换。所有的嘴部节点包括在一个矩形内（见图11-3），通过二维仿射转换得到，这需要计算已经提取的平面嘴部和二维嘴部对于三维人脸模型投射之间的差别，其中投射是在平移、比例和旋转三方面进行的。

仿射转换不能保证嘴部轮廓的匹配，为了保证上半嘴唇的自然形状，所有轮廓上的节点需要通过一个常数转换成提取的二维轮廓，该参数是通过估计平面人脸上半嘴唇外部轮廓线中间点和投射到三维人脸模型的二维中相应点之间的距离得到的。眼部转换的原则与嘴部转换的原则一致。对人脸模型处于两个椭圆中的眼部各节点进行仿射转换，然后根据已经提取的眼部轮廓来调整人脸模型的眼皮。然而，眼睛必须作为两个独立的物体来处理，即用两组独立的参数集合。另外，这里应用了线性插值来调试这些非边界节点。

图11-3 Candide模型的特征点示意图

2.非特征点的变换

在完成对特征点的三维坐标调整之后，模型调整即为确定非特征点的位置。我们利用适当的插值算法来计算非特征点的三维坐标。非特征点调整可采用的方法有自由变形、径向基函数内插、弹性匹配等。其中，自由变形算法较为复杂，径向基函数内插具有良好的平滑性，但需注意保证内插的平稳性。(www.xing528.com)

本系统利用径向基插值算法计算非特征点的三维坐标。这样，问题就转化为已知特征点x_i的位移f_i，s（x_i）=f（x_i），i=1，2，…，N，求径向基函数（RBF），即

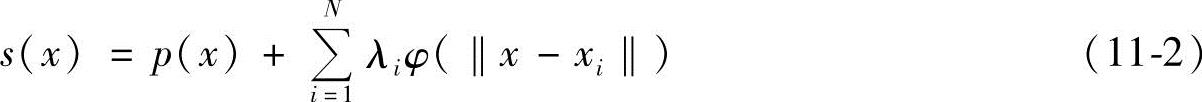
式中，s为径向基函数；自变量x为对应网格顶点的三维坐标，因变量为此点的位移量；p为低阶多项式；λ_i为RBF系数，即网格调整需要确定的模型参数；基函数φ（）为一个实函数。x_i是RBF中心，一般为与模型特征点对应的空间坐标。

令低阶多项式p的基为p={p₁，…，p_l}，对应的系数为c={c₁，…，c_l}，则式（11-2）以矩阵形式表示为

式中，A=[A_ij]；A_ij=φ（||x_i-x_j||）；p_ij=p_j（x_i）；i，j=1，2，…，N。

由此，线性方程可解得λ、c，从而确定了模型所有网格点的径向基函数s（x）。对于RBF的选取，在我们的实验中，选用了高斯函数，α取为1/64，即