基于改进MMI的HMM算法的面部表情识别技术

隐马尔可夫模型（HMM）是由Baum等人在19世纪60年代提出的，目前在模式识别与图像处理等领域得到了广泛的应用。由于HMM具有很强的动态时间序列建模能力，因此在处理时间序列问题上，HMM得到广泛的关注。传统的HMM参数估计方法采用Baum-Welch算法，它实际上是一种最大似然法（ML）。此外，人们还提出了其他训练算法，如最大互信息（Maximum Mutual Information）法、最小分类误差（Minimum Classification Error）法、校正训练（Corrective Training）法、最大模型距离（Maximum model distance）法等，各种方法都具有其自身的优点和缺点。参考文献[22，23]中提出的基于MMI训练算法将所有训练样本等同考虑，而实际上在整个训练过程中，不同训练样本对HMM参数估计的贡献是不相同的，基于这种情况，本小节定义了一个更为合理的MMI准则函数，称之为改进的最大互信息准则（Improved Maximum Mutual Information Estimation，IMMIE）函数，推导了HMM参数重估公式，并结合改进的光流算法，把它应用于面部表情识别。实验结果表明，该方法比MMI和Baum-Welch法性能更好。

1.IMMIE函数

本小节考虑的HMM均指连续隐马尔可夫模型（CHMM）。

设HMM表示为

λ=（π，A，B） （10-63）

式中，π为初始状态概率，π={π_i}，本小节只考虑左右结构的HMM，因此有π₁=1，π_i=0（i≠1）；A为状态转移概率，A={a_ij}；B为观察向量的混合高斯概率密度函数，B={b_j（o）}。

设Λ为HMM模型集，Λ={λ₁，λ₂，…，λ_V}，V为HMM个数；N_v和M_v分别为模型λv的状态数和每个状态所包含的高斯混合元个数，则训练样本集为

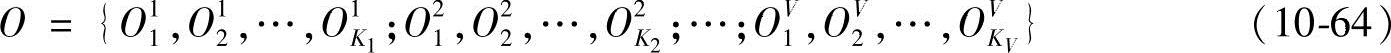
式中，O^v_k为模型λ_v的第k个训练样本；K_v为模型λ_v的训练样本数，且有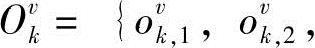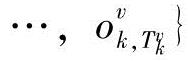；T_k^v为观察序列O^v_k的长度（v=1，…，V；k=1，…max（K₁，…，K_V））。最大互信息准则可以表示为

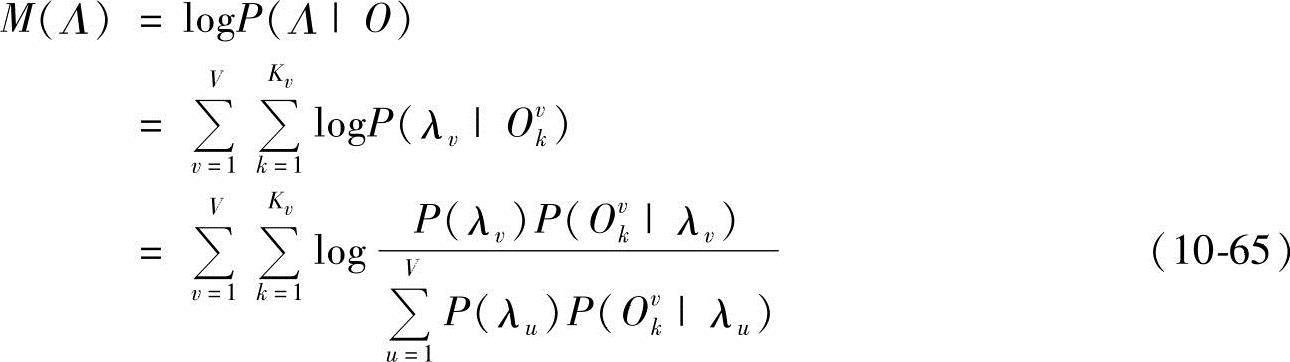
假定P（λ_v）=1/V，即每个HMM等概率出现，则式（10-65）可进一步写成

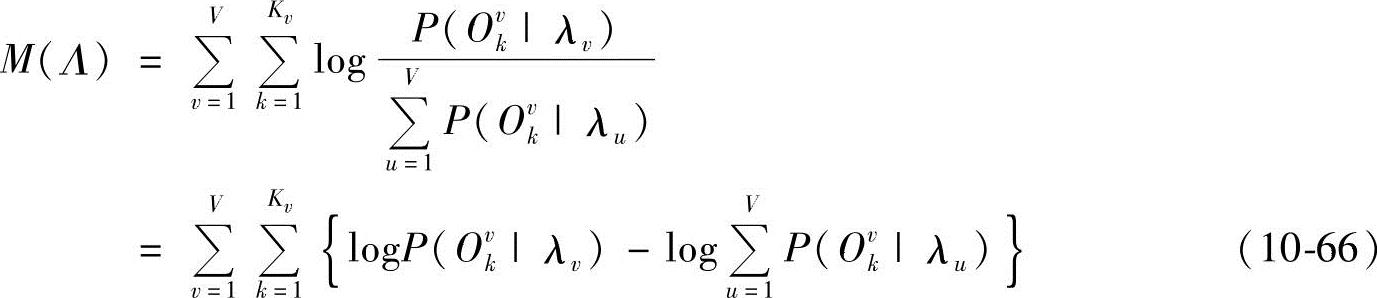
式（10-66）把每个模型对某一模型λ_v的影响同等对待，而实际上在各个训练样本下，每个模型对某一模型λ_v的参数估计的贡献是不同的，因此本小节引入加权而得到改进MMI准则函数为

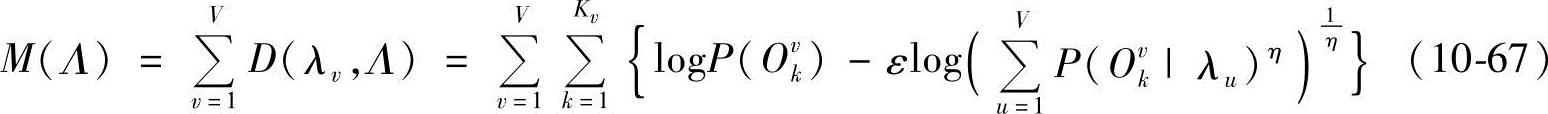
式中，0＜ε＜1，η＞0。

对比式（10-66）、式（10-67）式可知，参数η的引入可以有效控制不同样本作用下每个模型对当前模型的影响程度，使得不同样本对模型参数训练的贡献不同；当η=1、ε=1时，式（10-66）和式（10-67）等同，改变η值，各个模型对某个模型λ_v影响程度也发生变化，其中P（O^v_k|λ_u）越大，则在该样本下，模型λ_u对模型λ_v的参数估计影响越大，η值越大，这种影响就进一步加强，反之亦然；参数ε引入则可以有效控制所有模型对当前模型λ_v参数估计的综合影响程度，特别是，当ε=0时，式（10-67）退化成最大似然准则，此时基于式（10-67）的HMM模型参数估计算法等同于标准的Baum-Welch算法。

2.基于IMMIE的HMM参数估计算法

为了估计HMM参数，下面讨论有约束优化问题。

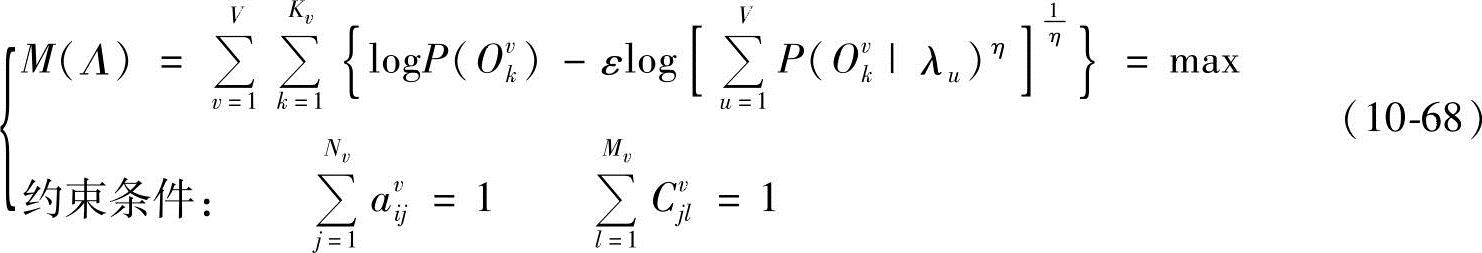
为求解优化问题式（10-68），构造拉格朗日函数为

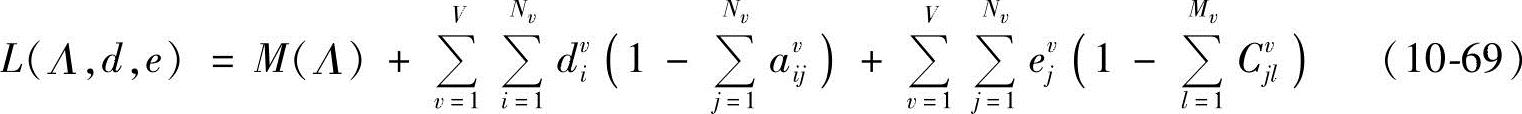
式中，d^v_i、e^v_i为拉格朗日乘子；a^v_ij为模型λ_v状态i转移到状态j的概率；C^v_jl为模型λ_v时状态j中第l个高斯混合元的混合系数；μ^v_jl和Σ^v_jl分别为与模型λ_v时状态j中第l个高斯混合密度函数N（o，μ^v_jl，Σ^v_jl）对应的均值向量和协方差矩阵（取对角型）。

令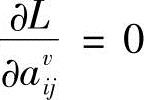、、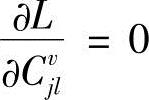、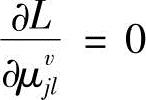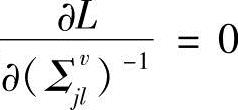，得到

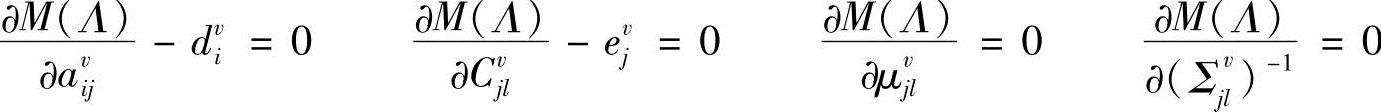
即

而

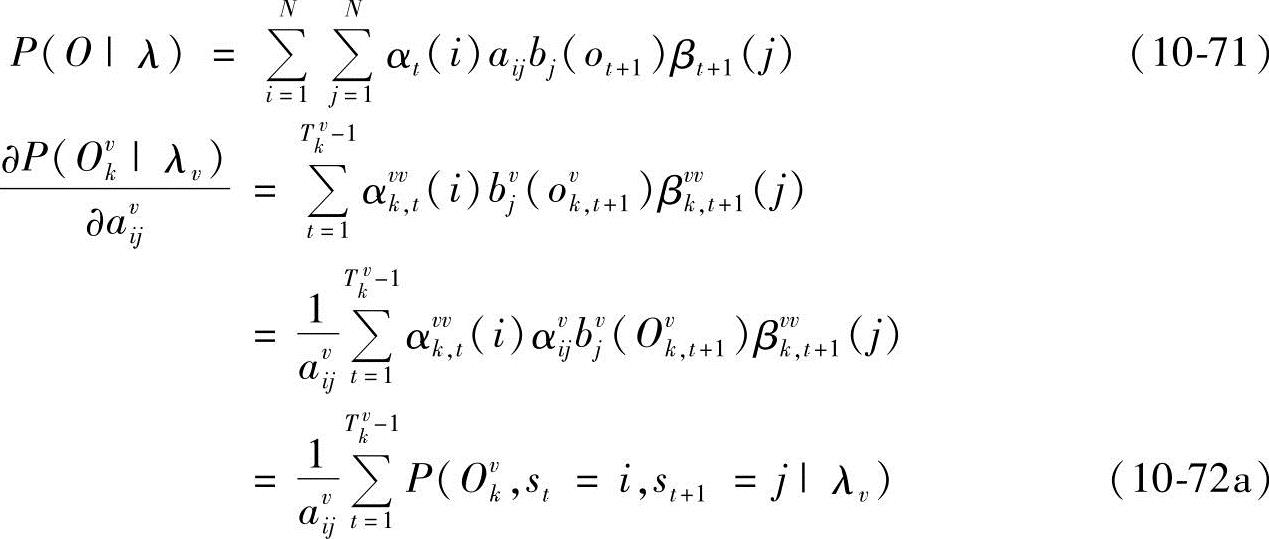
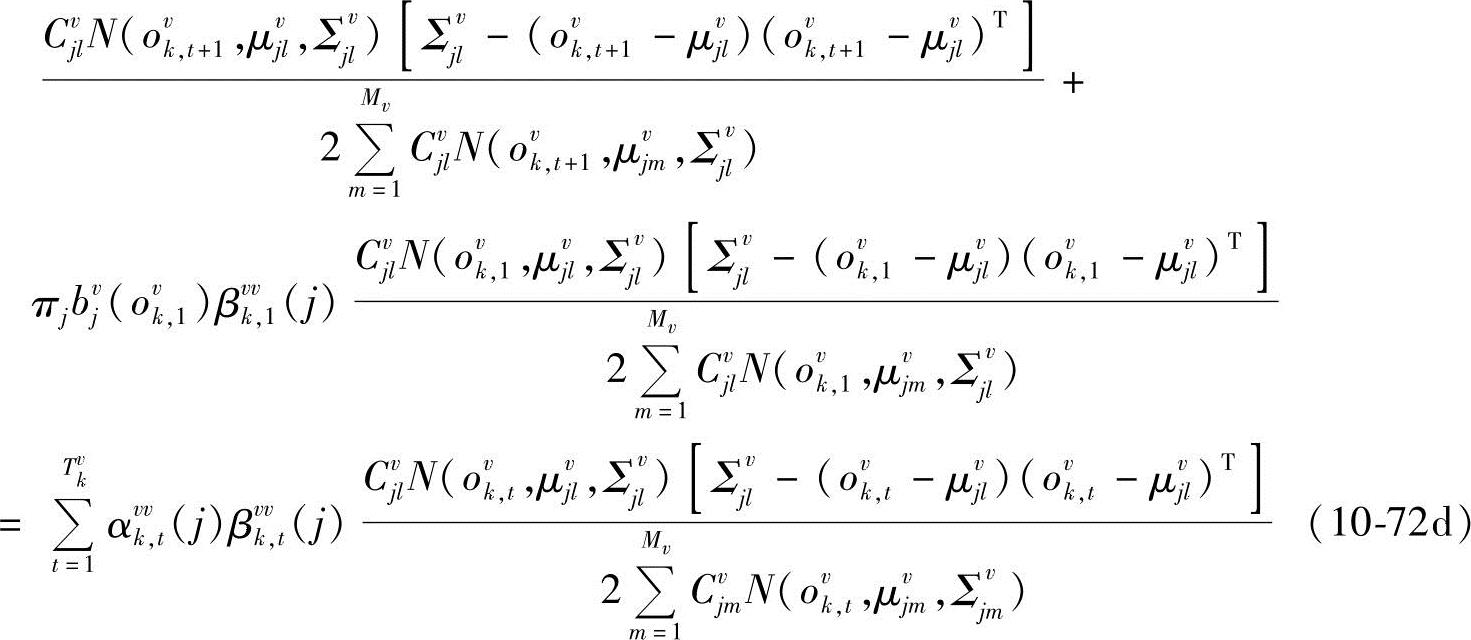
同理有

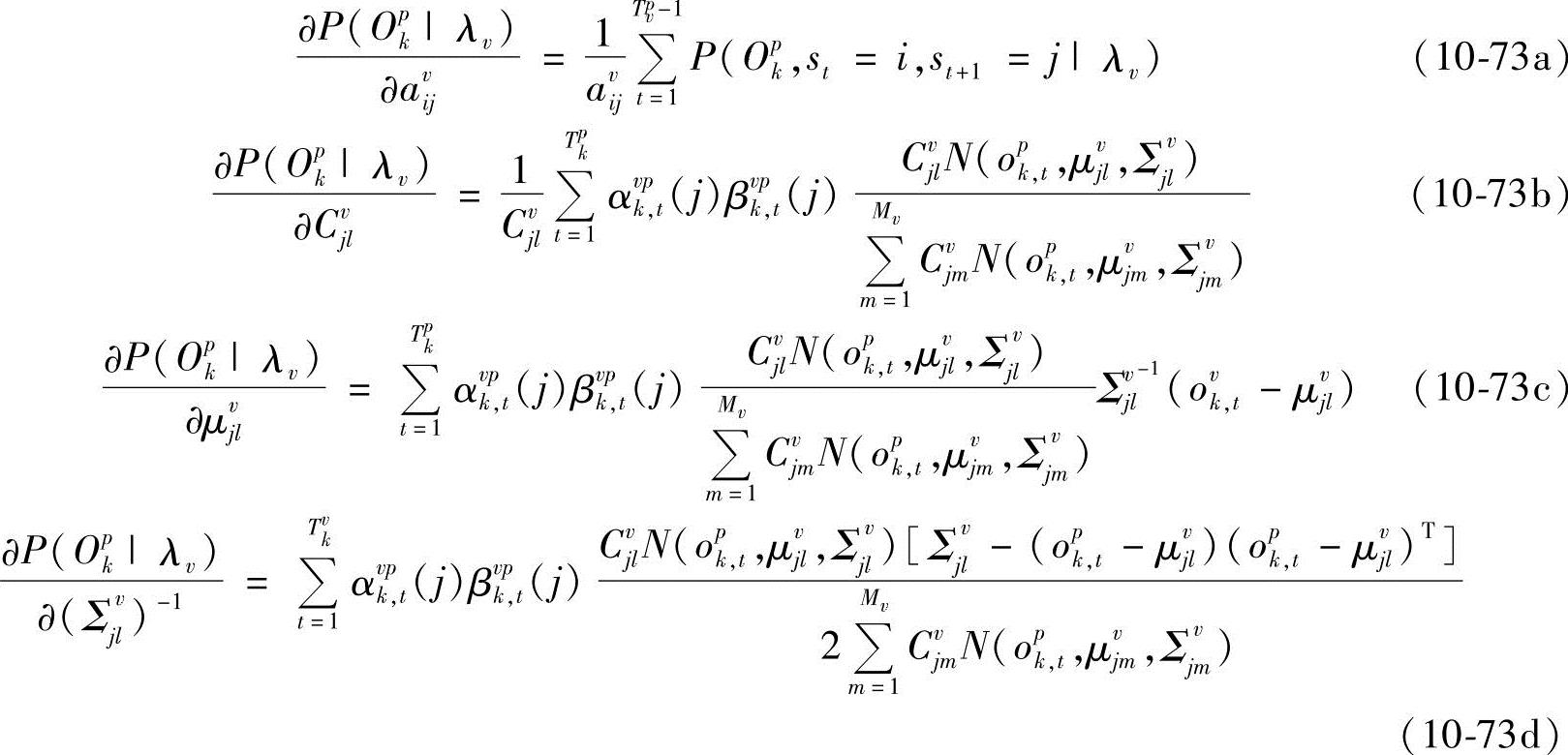
式中，α^vv_k，t（i）和β^vv_k，t（i）分别为给定第v类中第k个样本在模型为λ_v时，t时刻处于状态i的前向概率和后向概率；α^vp_k，t（i）和β^vp_k，t（i）分别为给定第p类中第k个样本在模型为λ_v时，t时刻处于状态i的前向概率和后向概率。由∂M（Λ）/∂a^v_ij-d^v_i=0得

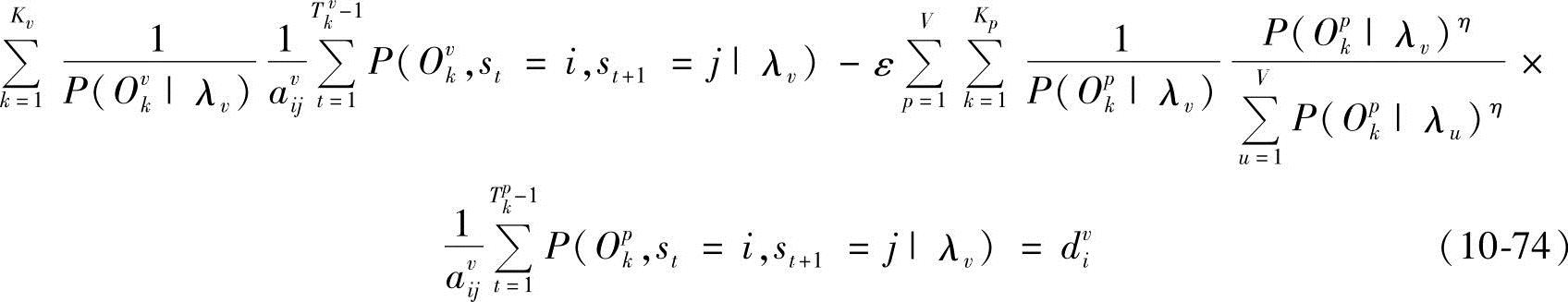
从而有

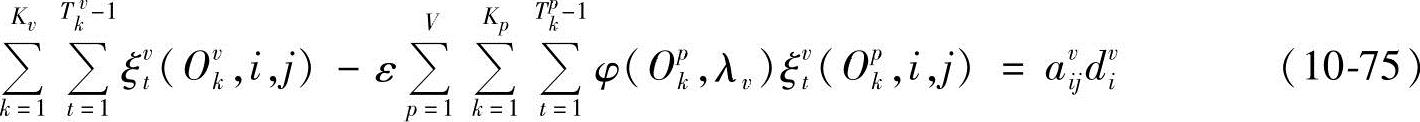
式中，ξ^v_t（O^v_k，i，j）和ξ^v_t（O^p_k，i，j）为过渡概率，ξ^v_t（O^v_k，i，j）=P（s_t=i，s_t+1=j|O^v_k，λ_v），ξ^v_t（O^p_k，i，j）=P（s_t=i，s_t+1=j|O^p_k，λ_v）；φ（O^p_k，λ_v）为相对输出概率，。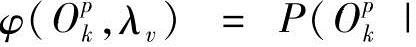

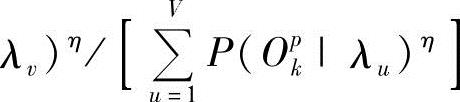将式（10-67）两边对j求和，并注意到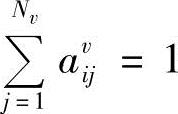，可得

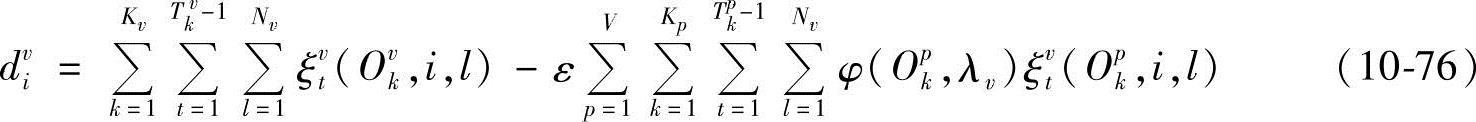
把上式代入式（10-75），可得

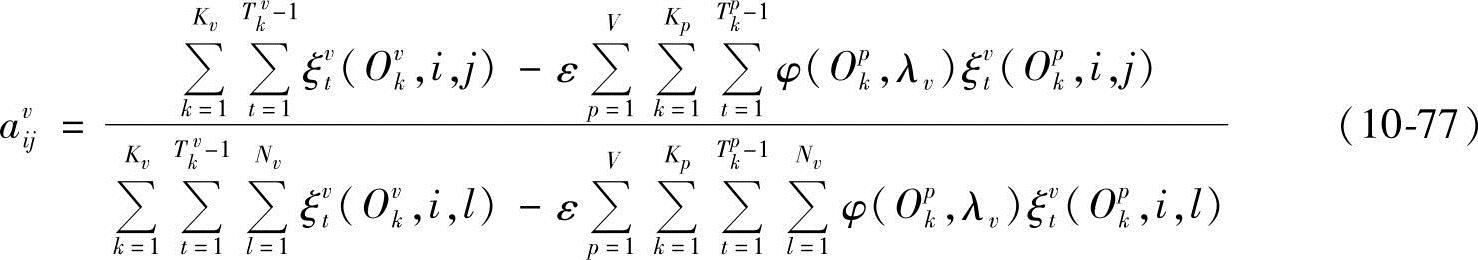
由∂M（Λ）/∂C^v_jl-e_j^v=0，得

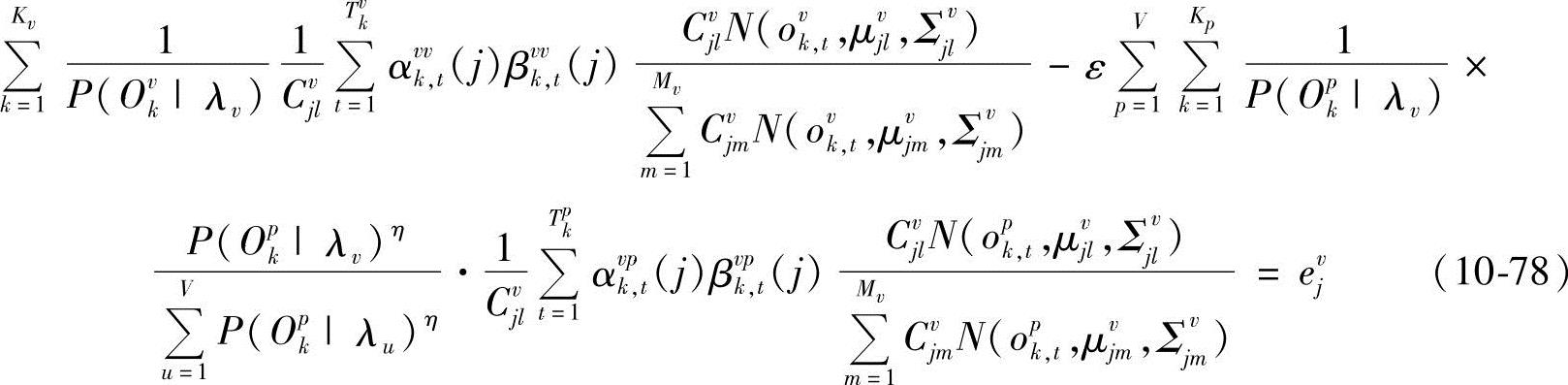
从而

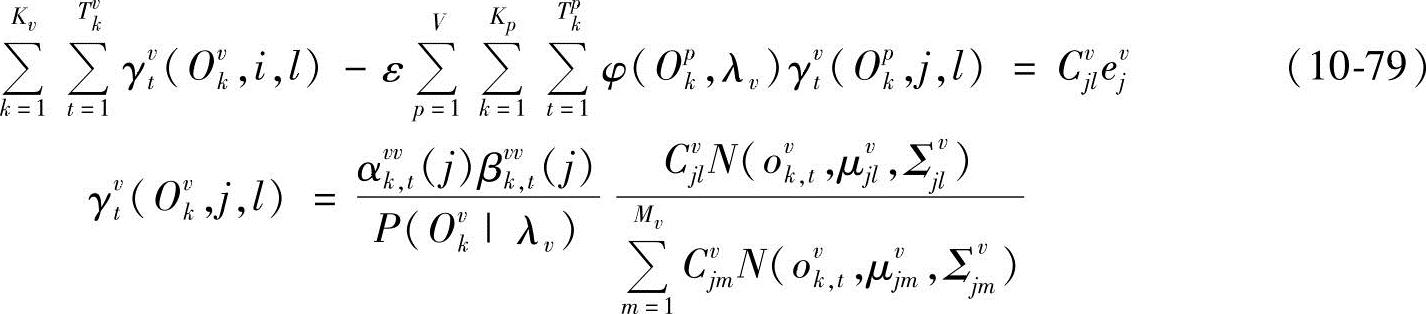
式中，γ^v_t（O^p_k，j，l）为混合输出概率。

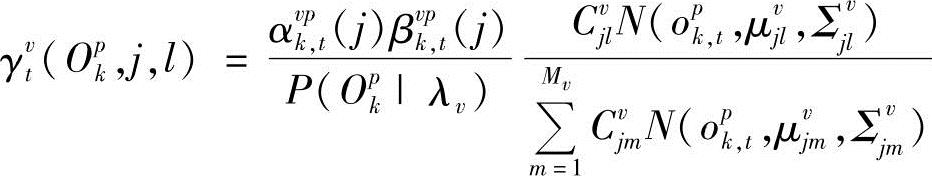
将式（10-79）两边同时对l求和，并注意到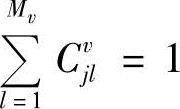，得

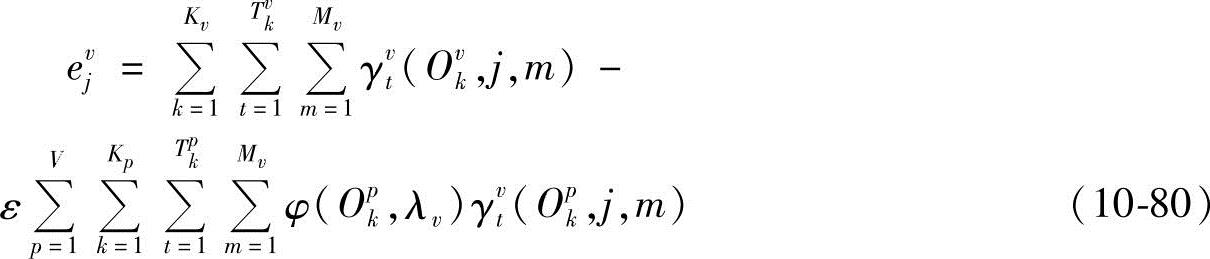
把式（10-80）代入式（10-79），得

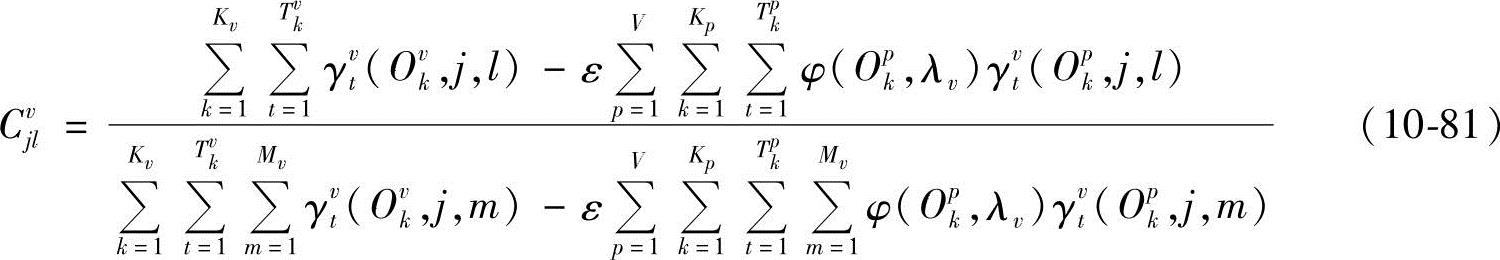
由∂M（Λ）/∂_μj^vl=0得

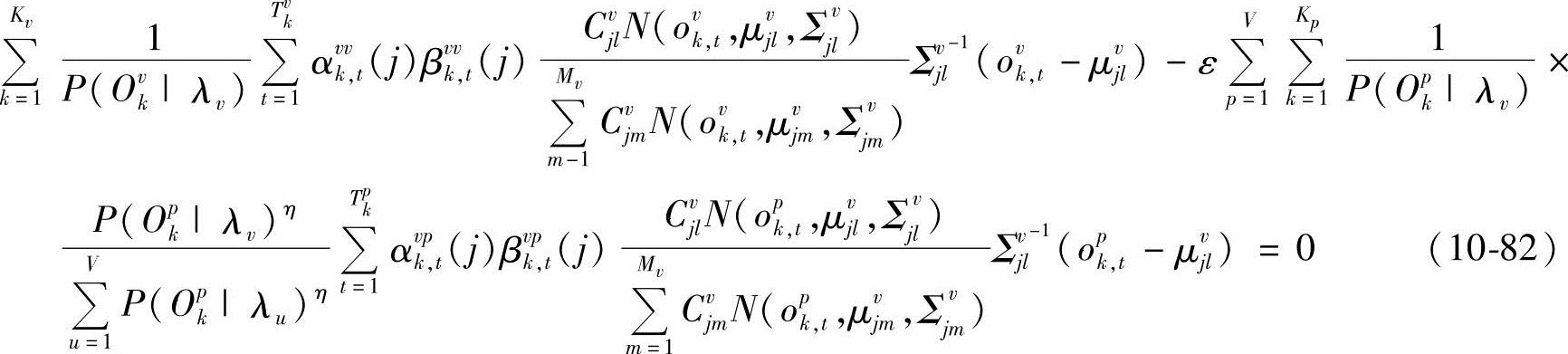
也即

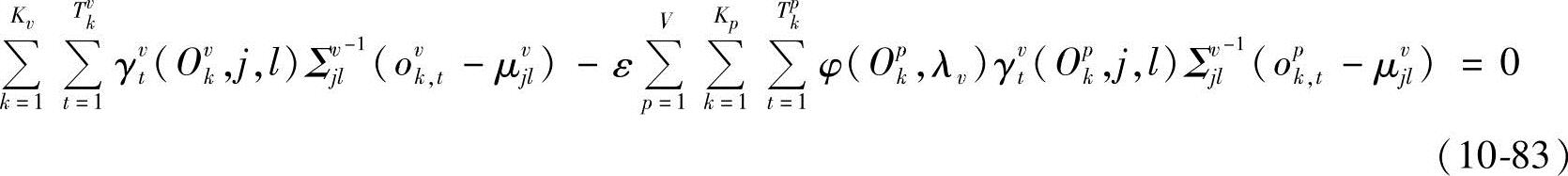
所以

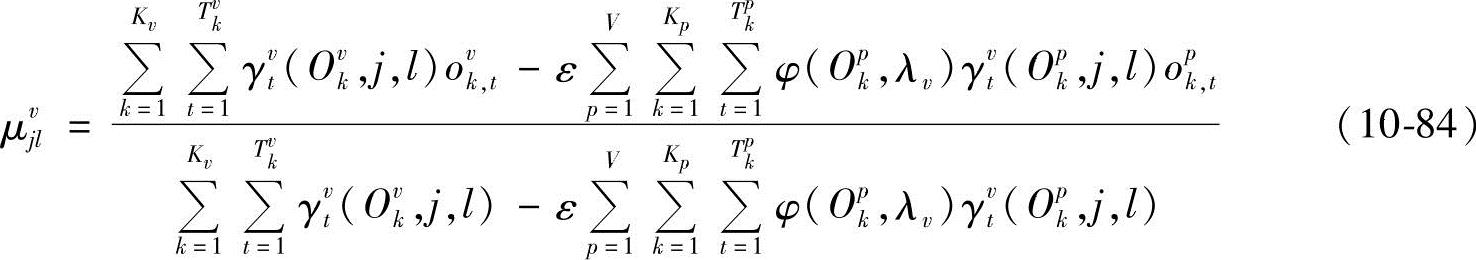
由∂M（Λ）/∂（Σ^v_jl）^-1=0得(www.xing528.com)

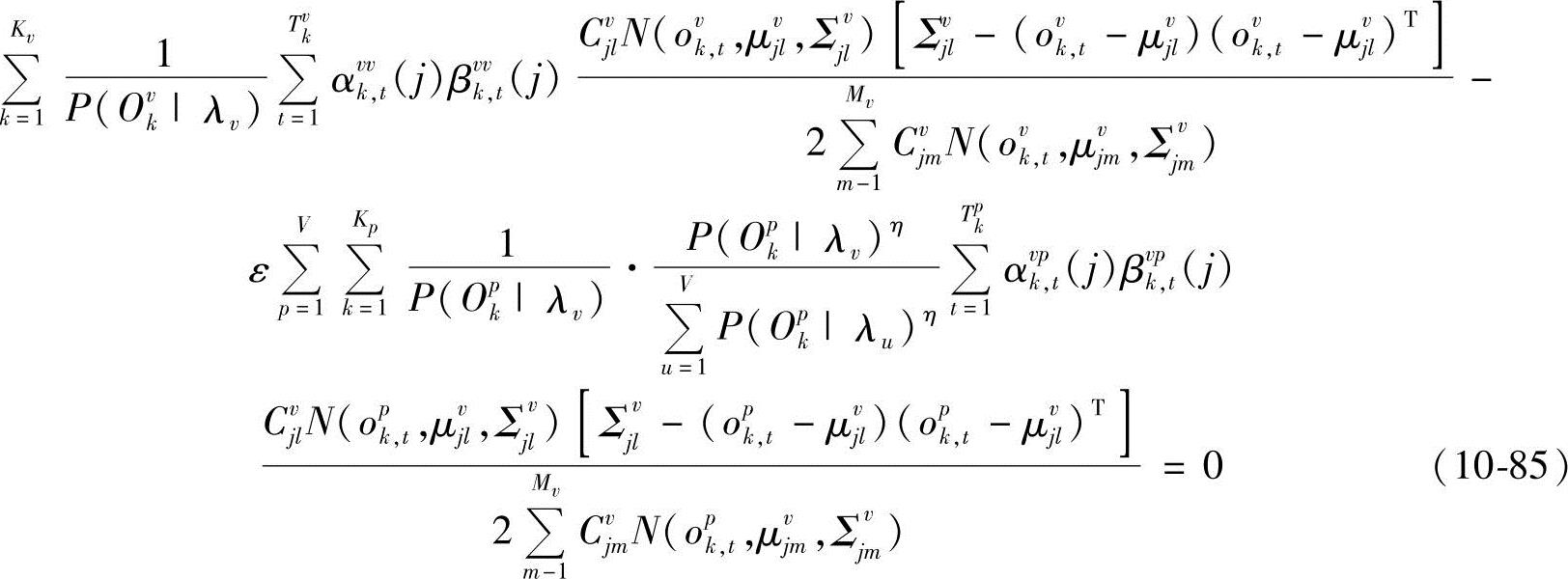
也即

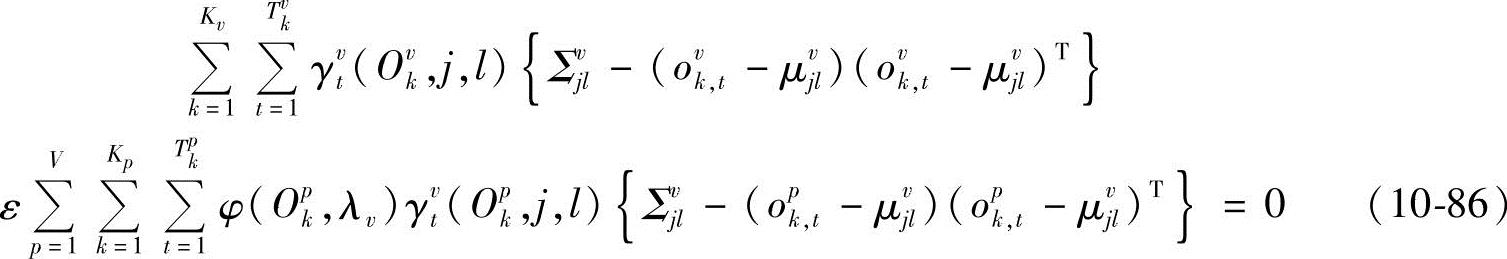
因此

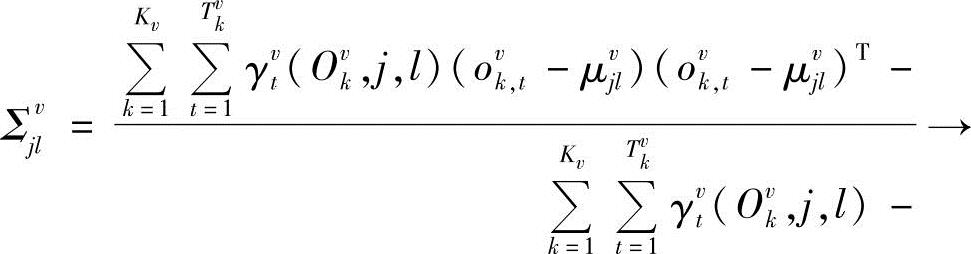
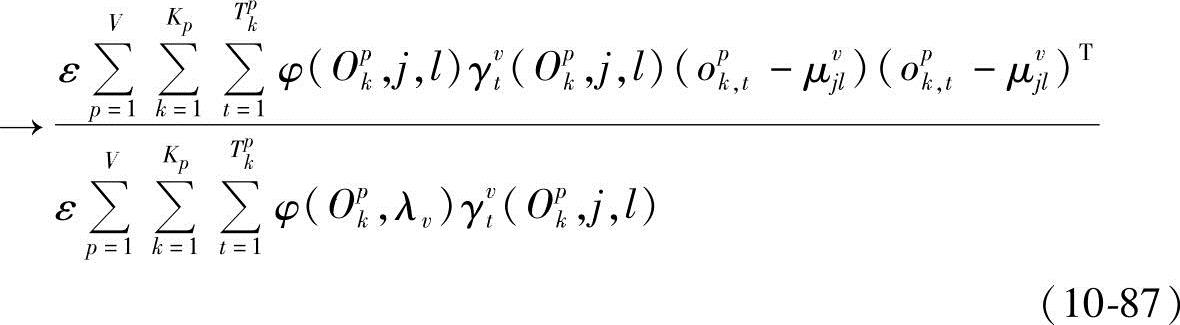
式（10-77）、式（10-81）、式（10-84）、式（10-87）即为改进的HMM参数重估算法。重新考虑式（10-66），当η→∞时，有

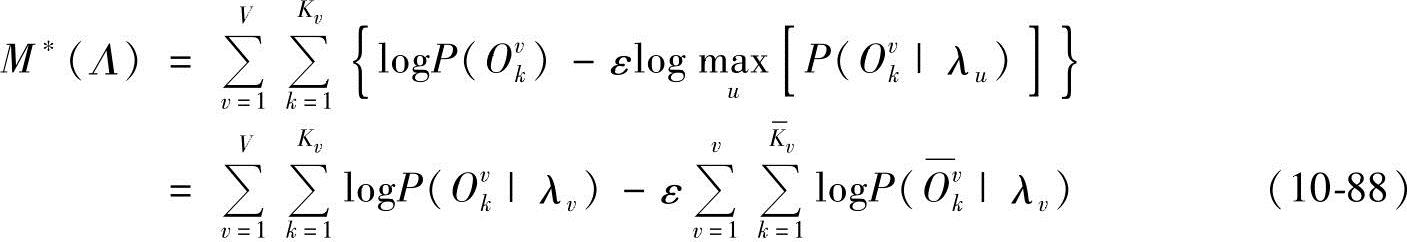
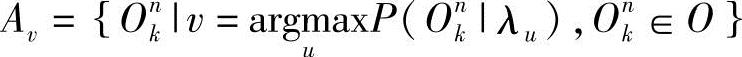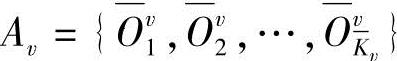设，不妨记，则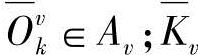为A_v中样本数。

对比式（10-66）和式（10-88）可以发现，对于式（10-66），所有HMM参数估计必须同时进行，对于式（10-88），各个HMM参数可以单独估计，其算法流程等同于Baum-Welch算法。

要使M^*（Λ）=max，可重复上述推导过程，得到

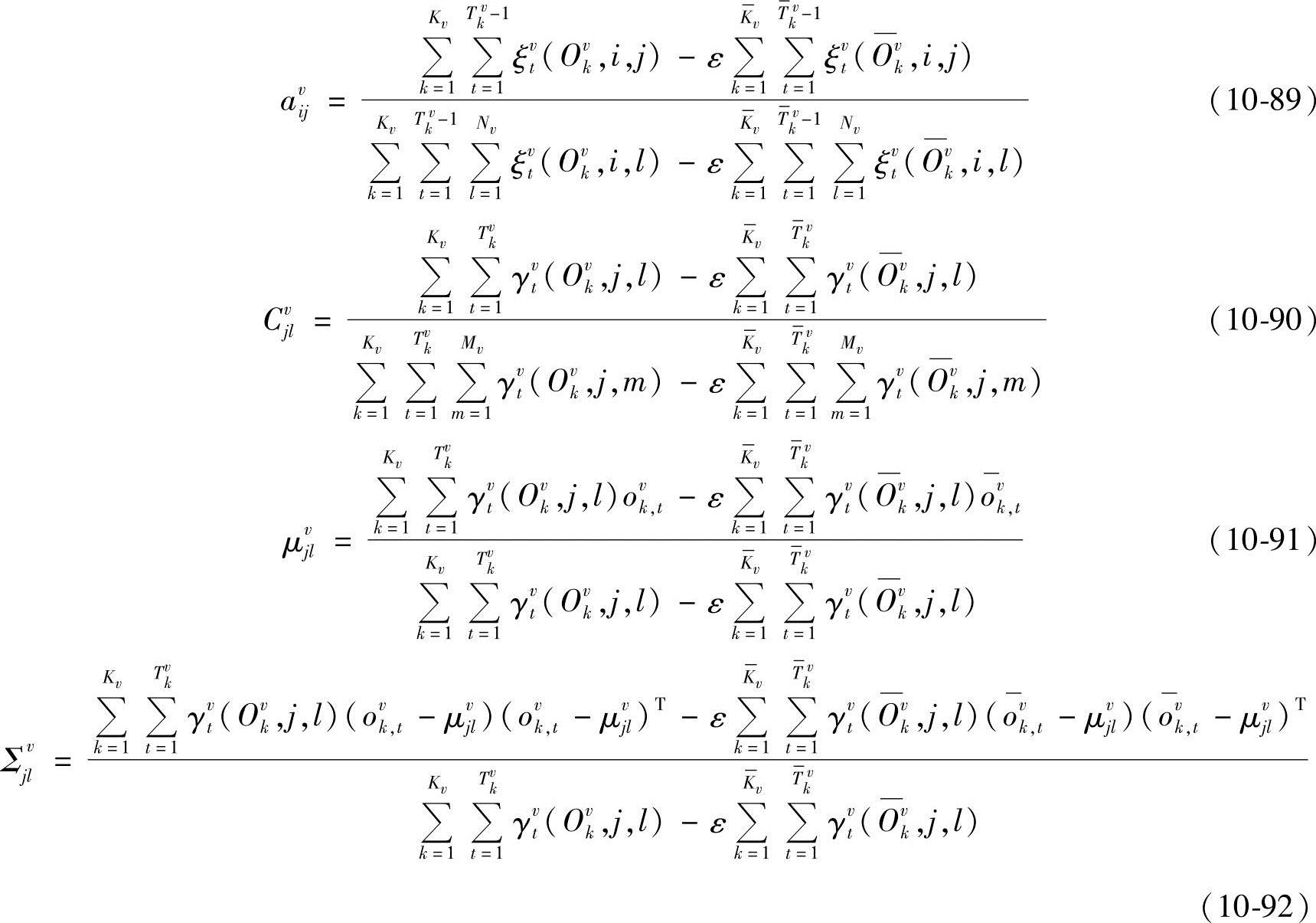
在参数重估过程中，为保证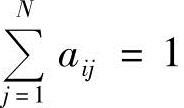、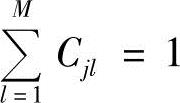，必须对每次估计的参数进行归一化处理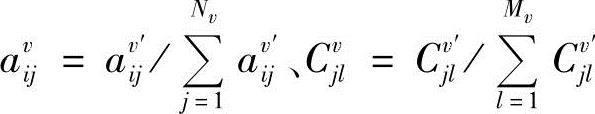：，其中a^v′_ij、C^v′_jl为重估值。

至此，改进的HMM重估算法基本完成，下面概括整个算法步骤如下：

1）HMM参数初始化。采用经典Baum-Welch算法估计HMM参数，把估计结果作为本小节IMMIE算法中HMM参数的初始值。

2）考虑到训练初期，训练样本在各个模型下输出概率相差不是很明显，而在训练后期，样本输出概率相差明显，因此对参数η进行自适应变化，即η（loop）=c^loop，其中，c为一常数，c＞1；loop为迭代步骤。

3）对每个训练样本，分别计算前向概率、后向概率、过渡概率、相对输出概率和混合输出概率，并对训练样本集重新分配，得到A_v。

4）利用式（10-77）、式（10-81）、式（10-84）、式（10-87）或式（10-89）～式（10-91）对HMM参数重估，并进行归一化处理。

5）判断参数估计是否达到预定迭代步数或精度，若是，则结束，否则转步骤（2）。

3.IMMIE参数估计算法在面部表情识别中的应用

面部表情识别系统的训练和识别流程如图10-19所示。

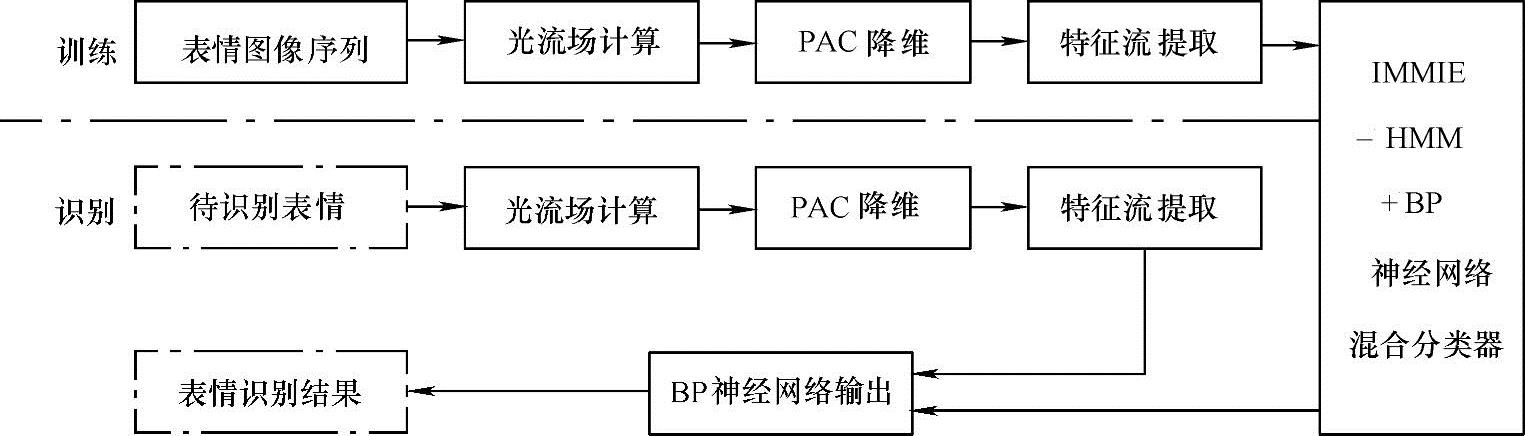
图10-19 基于IMMIE的HMM算法面部表情识别系统的训练和识别流程

为了提取面部表情的动态特征，先采用前面的改进光流法对面部表情图像序列计算光流场，得到表征面部表情变化的时间和空间信息。在得到光流场后，分别对水平方向u和垂直方向v的运动图像进行归一化和标准化，采用PCA法分别求取u方向和v方向的基底，表情图像的特征向量是有u和v分量的投影系数串联得到。对于含有某种表情变化的图像序列，先依次求出各帧图像中的速度场在各自u、v基底上的投影，并把u、v串联起来构成面部表情特征向量，整个序列就是面部表情特征流，用来作为HMM输入信号。

尽管HMM具有很强的时间信息处理能力，但是HMM也有自身缺点：首先，由于训练准则和算法的限制，使得它对模式的识别能力较差，虽然本小节对改变了HMM训练准则，使得HMM识别能力有所提高，但其识别能力相对于神经网络等分类器来说还是有差别；其次，HMM的拓扑结构和观测向量概率密度函数形式的先验选择往往和实际有出入；再有，认为状态序列由一个一阶马尔可夫链产生也不一定妥当等。与HMM相比，BP神经网络却具有很强的模式分类能力，且对输入的统计特性不必作出先验假设。

为了充分利用HMM和BP神经网络的优点，本小节构建了基于IMMIE的HMM和BP神经网络混合分类器，把BP神经网络作为二次分类器（见图10-20），其训练过程如下：

1）利用改进光流算法，计算面部表情图像序列的光流场，为降低数据维数，本小节对光流场利用主成分分析（PCA）进行数据压缩，得到面部表情的特征向量序列。

2）对上述得到的特征向量序列，利用IMMIE算法训练HMM。

3）把各个HMM输出概率组合成一个新的向量，并把它作为BP网络的输入信号，训练BP网络分类器。

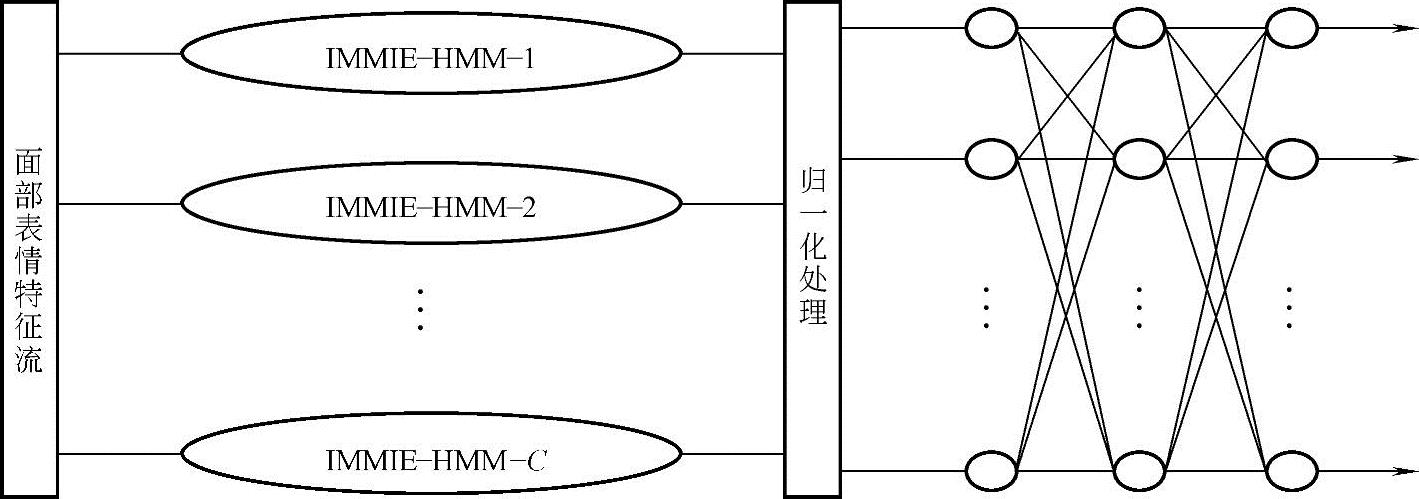
图10-20 IMMIE-HMM/BP神经网络混合分类器

4.实验结果及分析

在CMU人脸数据库中随机抽取了14个人的面部表情图像序列，并把10人的面部表情图像序列作为训练样本，其余4个人的面部表情图像序列作为测试样本。针对每种表情图像分别构建了不同的HMM，各个HMM均选择左右结构，其状态数为4，各个状态取高斯混合元个数为M=3，分别利用式（10-78）、式（10-81）、式（10-84）、式（10-87）和式（10-89）～式（10-92）训练HMM。把HMM输出作为BP神经网络分类器的输入信号，再训练BP神经网络分类器。其中，BP神经网络输入输出节点均为6个，其隐节点数通过实验调整。为便于比较，同时采用Baum-Welch法训练HMM，其测试结果如图10-21、图10-22所示，其中IMMIE1指基于式（10-77）、式（10-81）、式（10-84）、式（10-87）的HMM训练算法，IMMIE2指基于式（10-90）～式（10-93）的HMM训练算法，MMIE指基于式（10-66）的HMM训练算法。

图10-21所示为采用基于Hessian矩阵的光流算法提取面部表情的光流场，并采用PCA压缩得到面部表情特征流，构建了IMMIE-HMM/BP神经网络分类器。Ⅰ、Ⅱ、Ⅲ、Ⅳ分别为采用IMMIE1/BP神经网络、IMMIE2/BP神经网络、IMMIE/BP神经网络和Baum-Welch/BP神经网络四种方法的识别结果。方法Ⅴ为采用Lucas-Kanade光流法提取表情特征流和采用Baum-Welch/BP神经网络分类器得到的识别结果。

图10-22所示为采用非刚体光流算法提取面部表情光流场和采用PCA压缩得到面部表情特征流，构建了IMMIE-HMM/BP神经网络分类器。Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ分别为IMMIE1/BP神经网络+一阶div-curl约束光流法、IMMIE1/BP神经网络+二阶div-curl约束光流法、IMMIE2/BP神经网络+一阶div-curl约束光流法、IMMIE2/BP神经网络+二阶div-curl约束光流法和Baum-Welch/BP神经网络+Lucas-Kanade光流法的五种方法识别结果。

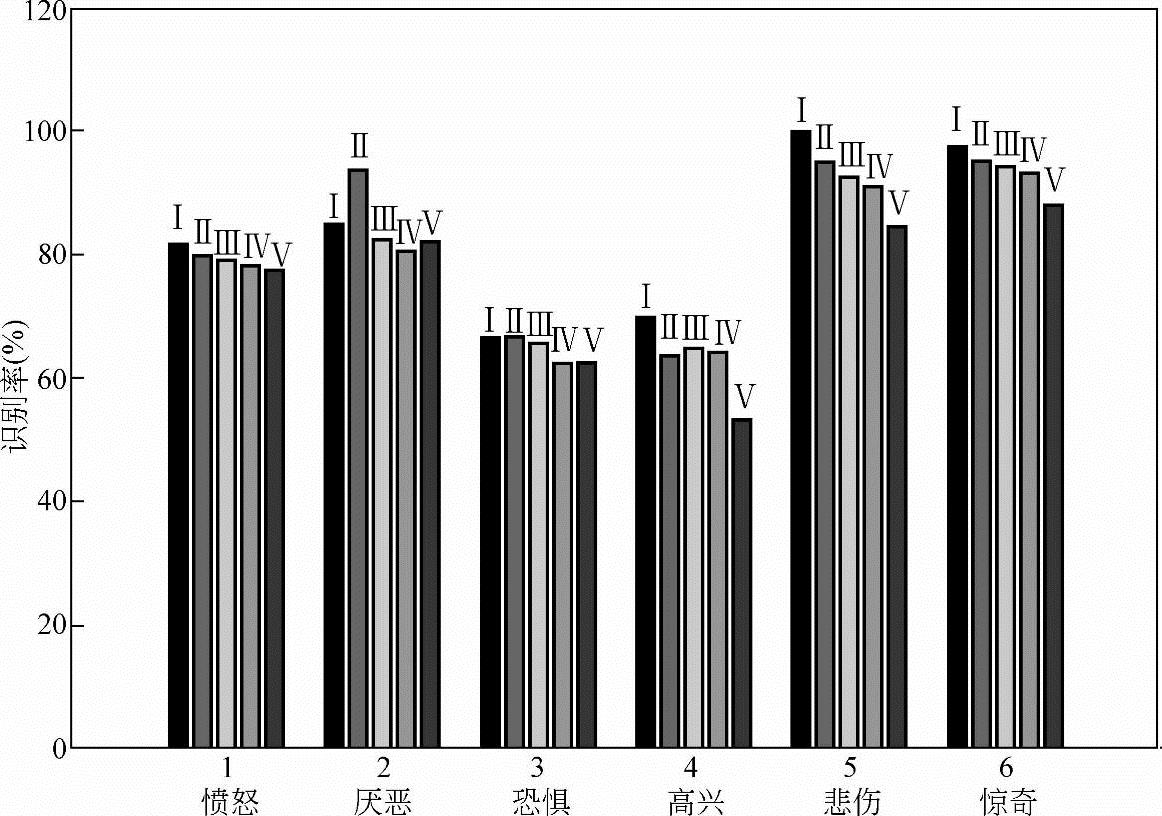
图10-21 基于Hessian矩阵光流法的表情特征提取下，IMMI法与其他方法的比较

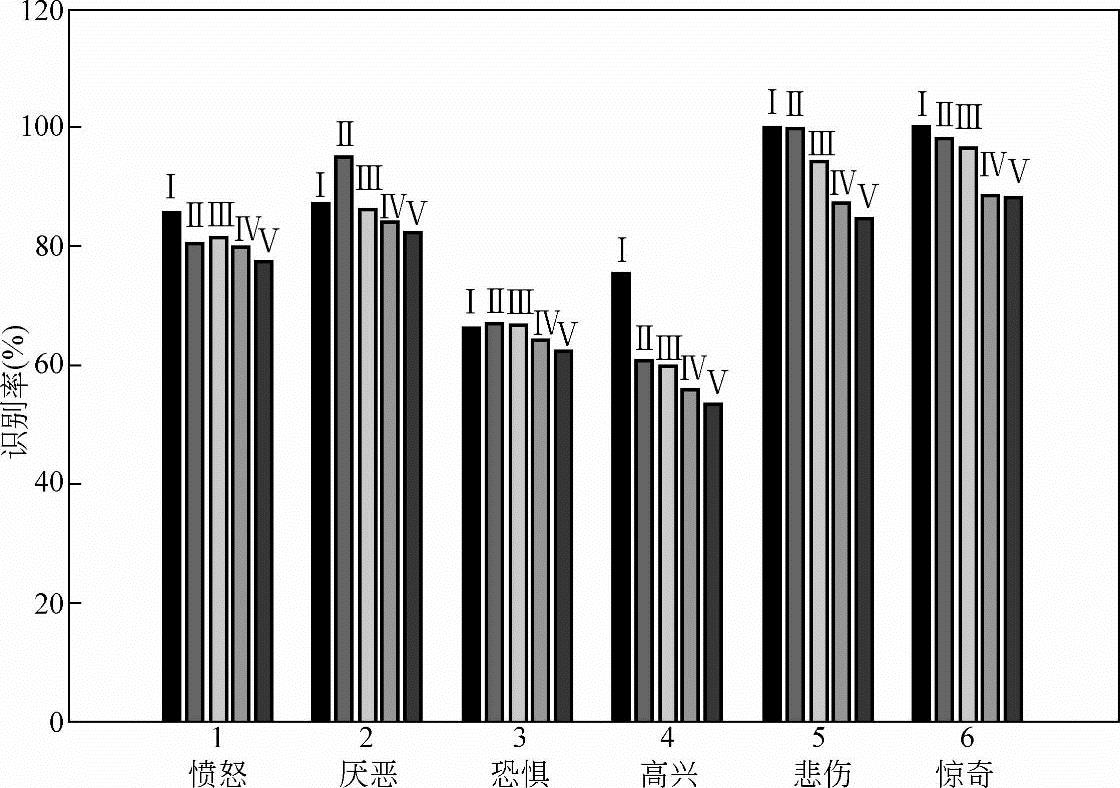
图10-22 基于非刚体光流法的表情特征提取下，IMMI法与其他方法的比较

由图10-21、图10-22可以看出，四种方法对悲伤、惊奇两类识别率较高。这主要是因为这两类有着较之于其他类别更明显的几何特征，如惊奇表情的眼睛张开得比较大，上眼皮被抬高，下眼皮下落，其嘴巴也大幅张开，以至于唇和齿分开。相比之下，高兴和恐惧这两类识别率普遍较低，只有60%左右，主要是因为高兴和恐惧在表现时脸部器官有较多相似运动特征，如两者的嘴巴部分都处于张开状态，且张开程度相似。在试验中发现，影响高兴识别率的主要是恐惧，而影响恐惧类表情识别率的除了高兴外，还有厌恶和愤怒两类表情。此外，由图也可看出，本节提出的两种方法（Ⅰ和Ⅱ）比其他方法（Ⅲ、Ⅳ和Ⅴ）对各类表情的识别效果均有不同程度的提高。由于测试时采用的是陌生人脸的六类表情，这些人脸在训练样本中未出现，由这点可以进一步体现该方法的鲁棒性。

如图10-23、图10-24所示，所有结果均是在采用10个人的表情图像序列作为训练样本时得到的，为了进一步探讨参与训练人数和测试结果的关系，我们进行了如下实验，分别采用6～10个人的样本参与训练分类器，其余人的表情图像序列作为测试样本，其结果如图10-23、图10-24所示。

图10-23中，“+”“o”“x”“□”表示的曲线分别为IMMIE1/BP神经网络、IMMIE2/BP神经网络、MMIE/BP神经网络和Baum-Welch/BP神经网络方法在采用Hessian矩阵光流法提取表情特征流后得到的分类结果，“▽”为采用Lucas-Kanade光流法提取表情特征流，并采用Baum-Welch/BP神经网络分类器得到的识别结果。如图10-24所示的“+”“o”“x”“□”“▽”分别为IMMIE1/BP神经网络+一阶div-curl约束光流法、IMMIE1/BP神经网络+二阶div-curl约束光流法、IMMIE2/BP神经网络+一阶div-curl约束光流法、IMMIE2/BP神经网络+二阶div-curl约束光流法和Baum-Welch/BP神经网络+Lucas-Kanade光流法等五种方法在不同训练样本集下的识别结果。

由图10-23、图10-24可知，随着参与训练的人数增加，各种方法识别率呈上升趋势，本小节提出的IMMIE/BP神经网络分类器明显优于其他分类器，特别是相对于Baum-Welch/BP神经网络+Lucas-Kanade光流法，这种优势就更为明显，可以预见，随着参加训练人数的继续增加，采用改进方法的识别率有望能进一步提高。

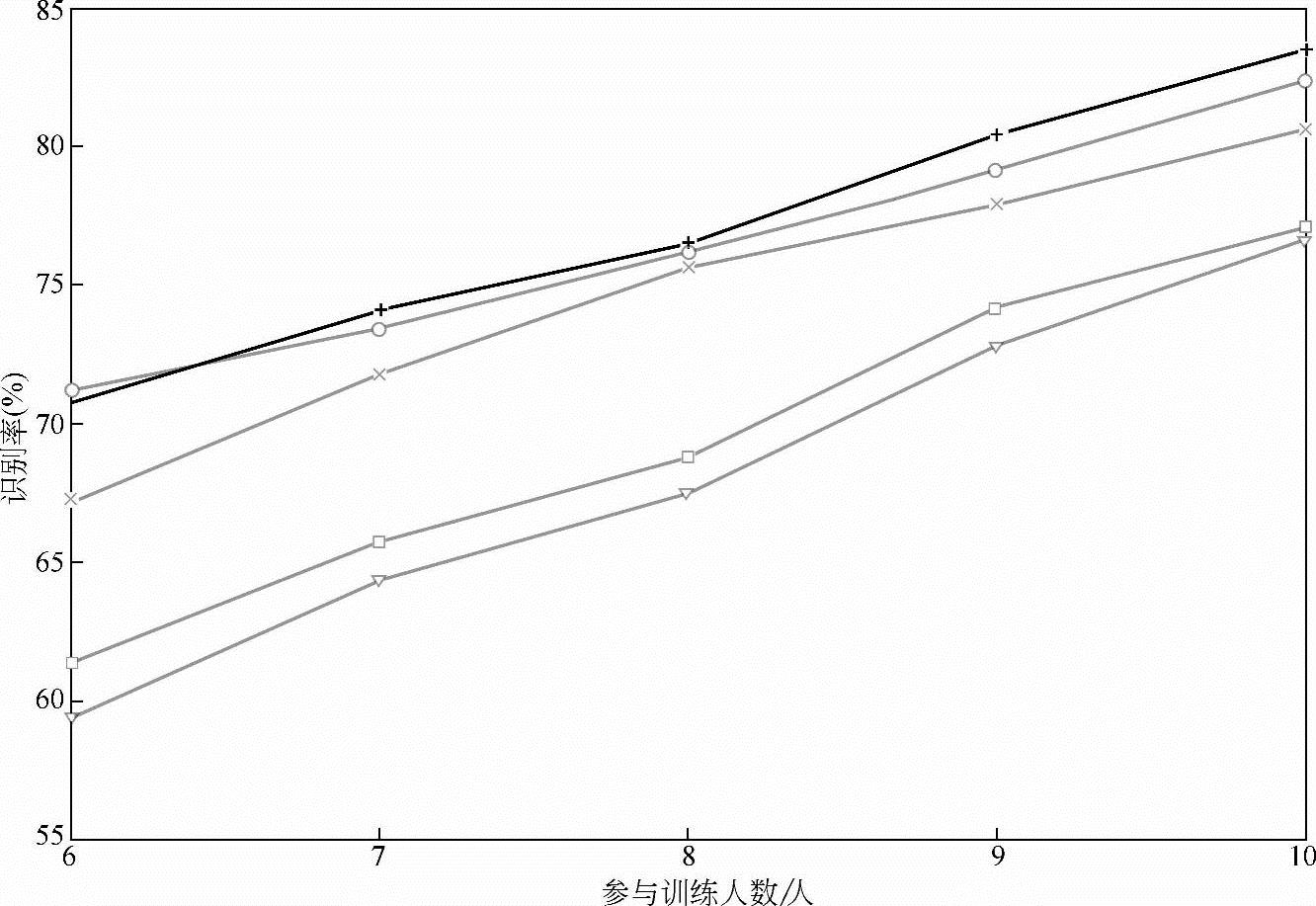
图10-23 基于Hessian矩阵光流法的表情特征提取下，参与训练人数与识别率关系曲线

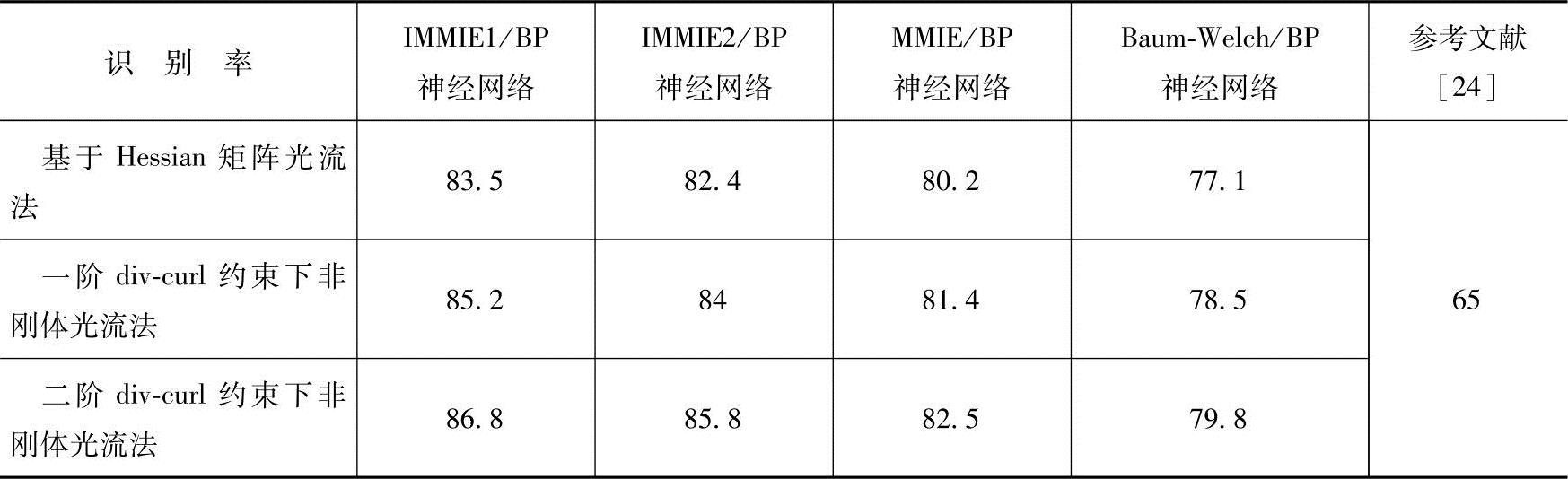
表10-6给出了不同方法在训练分类器人数为10时所有表情类的识别结果。同时，引入参考文献[24]所述的作为对比。参考文献[24]采用弹性图匹配法，使用了9个人的表情图像训练分类器，对陌生人脸表情的测试结果是65%左右，由于提取的只是表情图像的几何特征，参考文献[24]提供的方法实质上是一种静态的表情识别方法，而本节所述的方法是一种动态表情识别方法，因此识别效果有明显提高。同时，本节采用的是改进的HMM训练方法，因此本节所述的方法较之其他动态方法（IMMIE+BP神经网络和Baum-Welch+BP神经网络）也有明显改善。

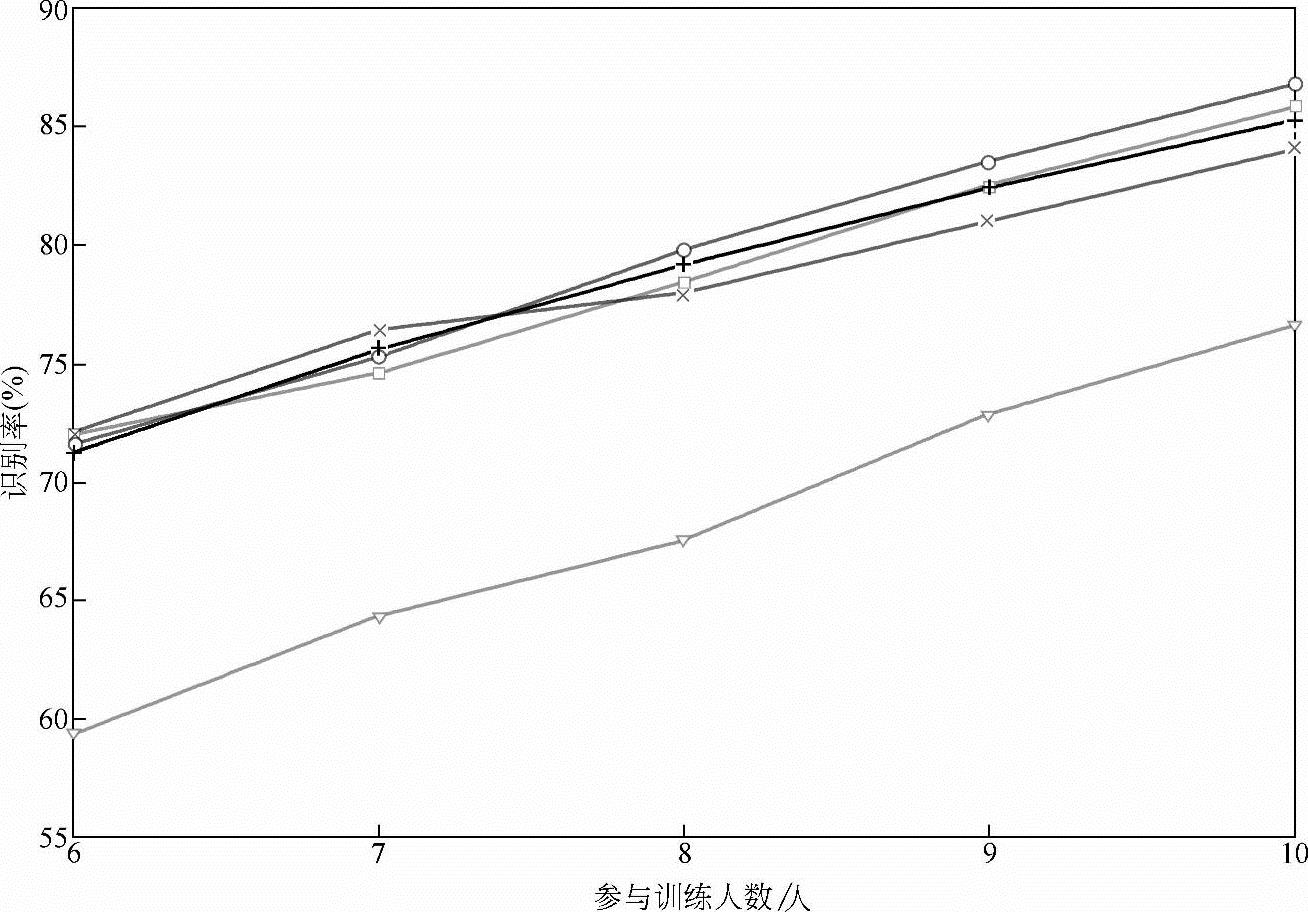
图10-24 基于非刚体光流法的表情特征提取下，参与训练人数与识别率关系曲线

表10-6 采用不同方法的面部表情识别结果比较（%）

5.小结

本小节提出了一种基于改进MMI的HMM训练算法，该方法相对于传统Baum-Welch算法，具有如下优点：

（1）模型准确性 Baum-Welch本质上是最大似然法，若要保证HMM训练的准确性，则需要大量样本。IMMIE算法充分利用了所有训练样本，因此在相同训练样本集下，采用改进MMI的HMM训练算法得到的模型更为精确。

（2）过训练 对于Baum-Welch法，每个HMM训练只利用了本类样本，由于受样本数量的限制且样本分布单一，往往使得HMM出现过训练，从而降低HMM泛化能力。而IMMIE算法，每个HMM训练不仅利用了本类样本，而且利用了其他类样本，这样使得参与训练的样本分布更为广泛合理，从而可以避免HMM出现过训练，提高了HMM的泛化能力。

（3）识别能力 Baum-Welch训练HMM只利用本类样本，因此该方法只是注重对本类样本的建模能力，而忽略了对其他类样本的鉴别能力，如果出现与本类样本相似的其他类样本，则该HMM就很难对该样本作出准确分类。IMMIE算法则不仅利用了本类样本，而且充分考虑了竞争类样本，把竞争类样本作为惩罚项引入了准则函数，从而可以大大提高识别能力。

（4）训练的不平衡性 对于Baum-Welch方法，如果某类样本很少或缺少，则与该类对应的HMM训练不充分或无法训练，不能有效对该类样本建模。而IMMIE算法则可有效避免这类情况发生，而且如果某类样本缺少时，还可以利用其竞争类的样本对该类HMM进行反向训练，这是与Baum-Welch一个显著的区别。