Hessian矩阵优化光流算法

传统的光流计算方法主要是基于灰度守恒和光流场的平滑性假设，但这些假设在阴影、边界和遮挡性的地方不再成立，为此提出相应的改进算法。

1.前向-后向光流方程

考虑下列方程：

I（x，y，t）-I（x+Δx，y+Δy，t+Δt）=0 （10-32）

可以得到

I（x，y，t）=I（x+Δx，y+Δy，t+Δt）

I（x，y，t+Δt）=I（x-Δx，y-Δy，t） （10-33）

对式（10-29）、式（10-30）分别进行泰勒展开，并忽略二阶及二阶以上项，得

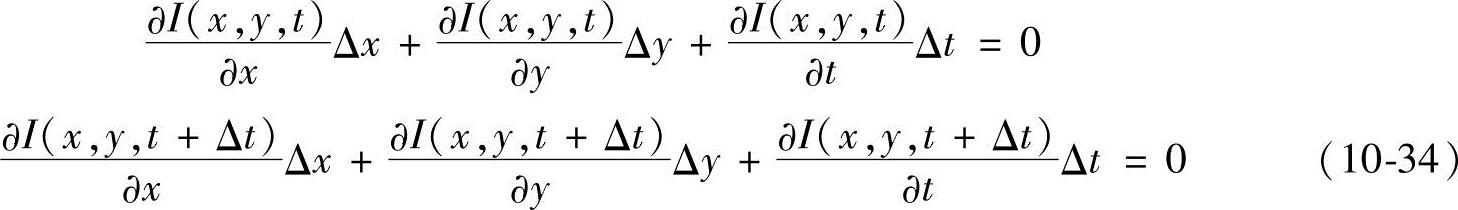
即

式中，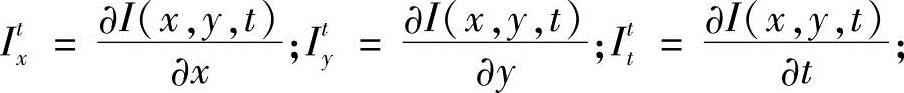

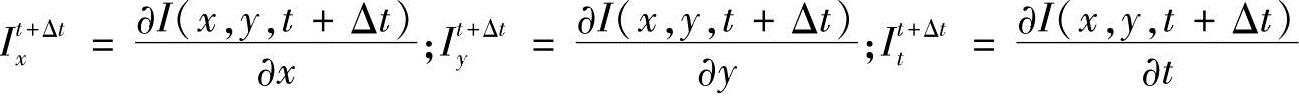
式（10-35a）、式（10-35b）即为前向-后向光流方程，可以合并为一个新的光流方程，即

I_x′u+I_y′v+I_t′=0 （10-36）

式中，I_x′=f₁（I_x^t，I_x^t+Δt），I_y′=f₂（I_y^t，I_y^t+Δt），I_t′=f₃（I^t_t，I^t_t+Δt）。

取：I_x′=αI_x^t+（1-α）I_x^t+Δt，I_y′=αI_y^t+（1-α）I_y^t+Δt，I_t′=αI^t_t+（1-α）I^t_t+Δt，α为一常数，根据性能指标式（10-36），可以求解出光流场（u，v）。

2.Hessian矩阵

尽管Lucas-Kanade光流法计算简单，光流估计精度较高，但它有一个致命缺点，即它假定邻域Ω内各像素点光流保持恒定，而且光流计算依赖于窗口权重函数，这意味着如果在邻域Ω内存在严重违反光流约束方程的点或邻域Ω运动不连续，将使得估计的光流可靠性严重降低。为此，引入Hessian矩阵判断领域Ω内每点对于基本约束方程的“良态性”。

对式（10-36）分别对x、y求偏导，可得

I_xxu+I_yxv=-I_txI_xyu+I_yyv=-I_ty （10-37）

即

定义Hessian矩阵为

Hessian矩阵的条件数：Cond（H）=||H||·||H^-1||=|λ_max|/|λ_min|，其中，λ_max、λ_min分别为Hessian矩阵H的最大特征值和最小特征值，可以通过Hessian矩阵条件数大小来判断方程式（10-38）解的稳定性，如果Hessian矩阵的条件数很大，则方程式（10-38）为病态方程，对应的Hessian矩阵秩很小，其解不稳定，计算的光流不可靠；如果Hessian矩阵的条件数接近1，对应的Hessian矩阵秩很大，方程式（10-38）为良态，其解鲁棒性较好。由此可以通过计算Hessian矩阵的条件数来剔除邻域Ω内的不可靠点。

3.梯度阈值处理

在复杂场景运动目标检测中，由于场景和运动目标的灰度梯度可能相差不大，使得运动目标轮廓处于模糊状态，在光流场的计算中，只有在灰度变化较大的地方，才能够获得比较精确的解，其他位置得到的解往往是不可靠的，计算的轮廓处光流不准确，也即基本光流约束方程在灰度梯度很小时不成立。为此引入梯度约束条件，设定灰度梯度阈值T，在灰度梯度大于阈值T的像素点计算光流。

4.基于Hessian矩阵的光流算法

Hessian矩阵的条件数很好地刻画了线性方程式（10-38）解的稳定性，而且条件数越大，对应的Hessian矩阵的秩越小，为此可以先利用Hessian矩阵剔除邻域Ω内的不可靠点，并把各点对应条件数的倒数作为该点权值，其算法如下：

1）计算图像中每点的一阶和二阶梯度。

2）分别计算每点对应Hessian矩阵的秩det（H）和条件数Cond（H），设定阈值为τ，则：(www.xing528.com)

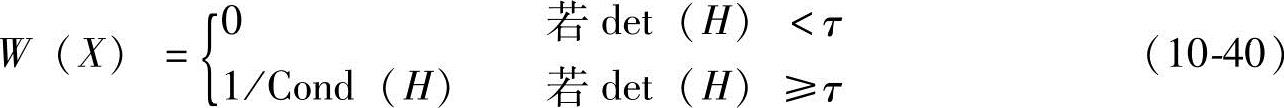
并对每个邻域Ω内的W（X）进行归一化处理。

3）采用加权最小二乘法求解式（10-35）中光流场（u，v）。

为了验证上述算法的有效性，本小节采用了一组合成图像序列和两组真实图像序列进行实验。其中，合成图像序列相邻帧间的真实光流已知，通过采用上述算法对其估计光流，然后与真实光流比较，作出定量评估。对于光流场V=（u，v）^T，把它写出一个三维的方向向量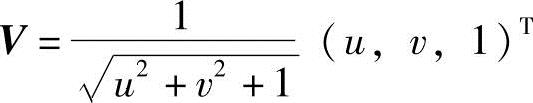，真实光流V_c和估计光流V_e之间的光流角误差可以表示为

ψ_E=arccos（V_c·V_e） （10-41）

平均误差为

式中，N为光流场的像素个数。对光流场标准角偏差定义为

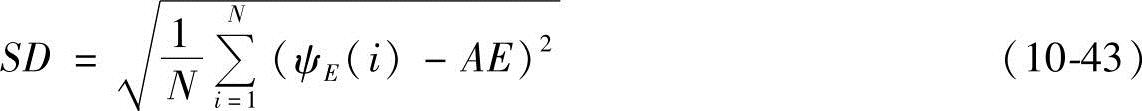
参照Barron等人的做法，本小节亦在估计光流之前，采用了标准差为1.5像素/帧的时空高斯滤波器平滑图像序列，这有助于削弱时间噪声和输入中的量化效应。

图10-11a、b分别是Translating Trees图像序列的第7、8帧，该图像序列以1.73～2.26的流速向右运动，运动方向平行于水平轴。图10-11c所示是利用本小节所述方法计算的第8、9帧之间的光流场。可以看出，光流方向基本跟真实光流一致，大小有些差别，表10-4给出了本小节所述改进算法和其他方法计算的光流平均角误差和标准角偏差的对照。

图10-11 Translating Trees图像序列与光流场

a）第7帧图像 b）第8帧图像 c）光流场

表10-4 对TranslatingTrees序列，本小节介绍的改进算法与其他算法比较

图10-12所示是Rubic Cube序列实验结果，其中图10-12a、b为Rubic Cube序列中的第9、10帧，图10-13a是采用标准Lucas和Kanade光流法得到的Rubic Cube序列中第9、10帧光流场，噪声含量比较多；图10-13b为采用本小节方法得到的光流场，显然该光流场比较准确地反映了Rubic Cube图像序列的运动信息，比图10-13a噪声少得多。

图10-12 Rubic Cube图像序列中第9、10帧图像

a）第9帧图像 b）第10帧图像

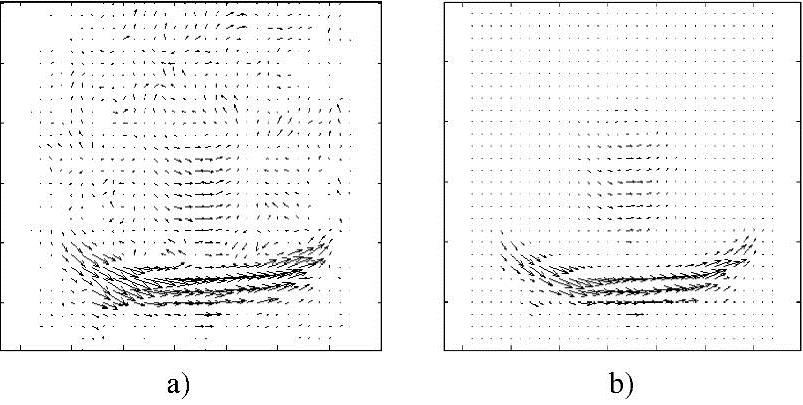
图10-13 计算的Rubic Cube光流场

a）基于Hessian矩阵光流法 b）基于Lucas和Kanade法

利用本节方法对卡耐基梅隆大学的人脸表情库进行测试，图10-14所示为一愤怒表情序列图像。其中，图10-14a、b所示分别为该序列图像的第11、13帧，愤怒表情主要体现在眼睛、眉毛和嘴巴：眉毛紧皱、上下眼皮紧张，眼睛可能鼓起、上下嘴唇紧闭，图10-14c所示为采用本小节方法计算的光流场。图10-15所示为一惊奇表情序列图像。其中，图10-15a、b所示分别为该序列图像的第5、6帧，惊奇表情主要体现在眼睛睁大、上眼皮抬高、下眼皮下落、嘴巴张开、下颚下落，从图10-15c可以看出，该光流场基本反映了眼睛及嘴巴的运动趋势。但由于人脸运动为非刚体运动，其运动过程中发生了变形，导致图像灰度值发生严重变化，因此相对于刚体运动的光流场估计，非刚体运动光流场估计准确度稍差。

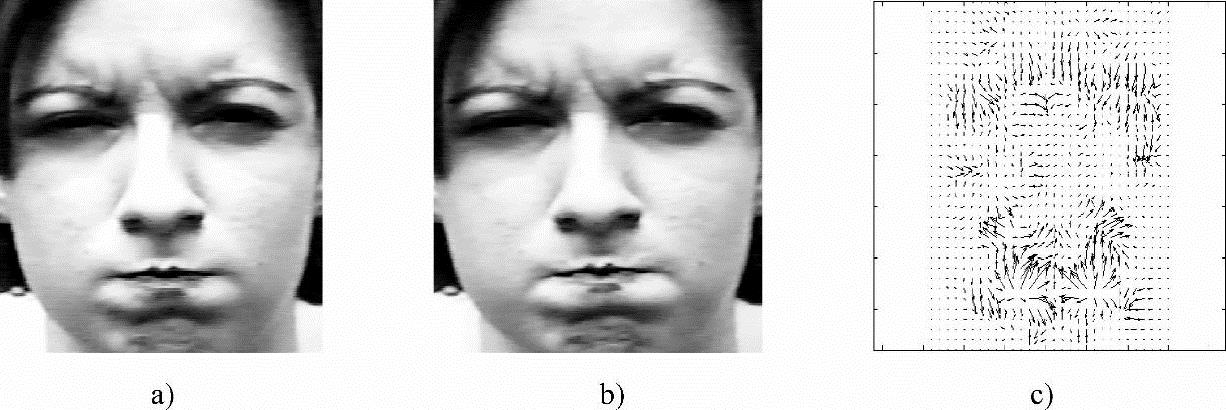
图10-14 愤怒表情图像序列与光流场

a）第11帧图像 b）第13帧图像 c）光流场

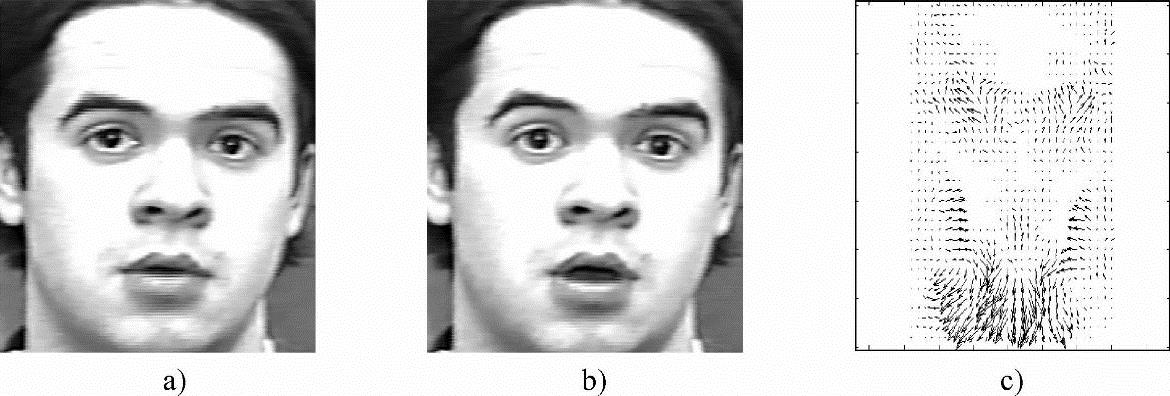
图10-15 惊奇表情图像序列与光流场

a）第5帧图像 b）第6帧图像 c）光流场

本小节详细讨论了光流法在面部表情序列图像分析中的应用，利用改进的光流算法计算了面部表情图像的光流场，针对传统光流法在阴影、边界和遮挡性的地方灰度守恒和光流场的平滑性假设不再成立这一问题，引入前向-后向光流方程，计算其Hessian矩阵，并把Hessian矩阵的条件数与Lucas-Kanade光流法中的加权阵相结合，有效地消除局部邻域中不可靠的约束点，同时进一步提高光流约束方程解的稳定性。