基本光流计算方法简介

光流法是一种重要的运动图像分析方法，在最近20年得到了较大发展，研究者提出了多种不同的光流法作为改进算法，主要可以分为四类：时空梯度法、块匹配方法、基于能量方法和基于相位分析法，其中时空梯度法最为常见。

1.时空梯度法

时空梯度法又称为微分法，它是利用图像序列灰度，即时空梯度函数，来计算每一图像点的速度向量。设I（x，y，t）为t时刻图像点（x，y）的灰度；u、v分别为该点光流向量沿x和y方向的两个分量，且有u=dx/dt、v=dy/dt。根据图像灰度一致性假设，有d（x，y，t）/dt=0，则

I_xu+I_yv+I_t=0 （10-16）

写成向量形式有

式中，I_x、I_y、I_t分别为参考像素点的灰度值沿x、y、t三个方向的偏导数；ΔI为图像灰度的空间梯度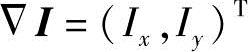；V为光流向量，V=（u，v）^T。

基本约束方程限定了I_x、I_y、I_t与光流向量的关系，由于该方程有两个未知数u、v，则其解为非唯一。用一个方程来限定两个未知量，本来就是一个不适定问题，因而为求解V的两个分量必须附加另外的约束条件。

Lucas和Kanade假设在一个小的空间邻域Ω上，运动向量保持恒定，然后使用加权最小二乘法（Weighed Least-squares）估计光流。在一个小的空间邻域Ω上，将光流估计误差定义为

式中，W²（x）表示窗口权值函数，它使邻域中心区域对约束产生的影响比外围区域更大。式（10-18）的解为

U=（A^TW²A）-1A^TW²B （10-19）

式中，在t时刻的n个点X_i∈Ω下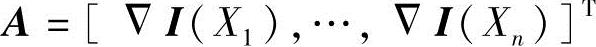，，W=diag[W（X₁），…，W（X_n）]，B=-[I_t（X₁），…，I_t（X_n）]^T。

Horn和Schunck将梯度方程式（10-17）和一速度场整体平滑约束组合在一起来约束待估速度V=（u，v）^T，最后得到了一个稠密的光流场。

上述算法的实现相对简单，计算复杂性较低，然而这种技术存在着严重缺陷。首先，图像灰度一致性假设对于许多自然图像序列来讲都是不合适的，尤其是在图像的遮挡边缘处和（或）当运动速度较高时，基于灰度一致性假设的约束方程式（10-9）存在着较大误差。其次，在图像的遮挡区域，速度场是突变的，而总体平滑约束则迫使所估计的光流场平滑地穿过这一区域，此过程平滑掉了有关物体形状的非常重要的信息。第三，时空梯度法的一个要求是I（x，y，t）必须是可微的，这暗示着需对图像数据进行时空预平滑，以避免混叠效应；而且数值微分的求取具有病态性，如果处理不当，将对最终的速度估计产生显著影响。

2.匹配法

匹配法实质上是在图像序列的顺序图像对之间实施的一种对应，它将光流定义为使得不同时刻图像区域之间产生最佳拟合的位移。给定两帧顺序图像I₁和I₂，对于图像I₁中的每个像素点（x，y），以此像素为中心形成一个大小为（2n+1）×（2n+1）的相关窗W_c。围绕图像I₂中的对应像素点（x，y）建立一个尺寸为（2N+1）×（2N+1）的搜索窗W_s。搜索范围可根据有关两图像间最大可能位移的先验知识来确定。于是可用下面的误差平方总和（SSD）来计算搜索区域上的（2N+1）×（2N+1）误差分布，即

然后将此误差分布转换成指数形式的响应分布，得

R（u，v）=exp[-kε（u，v）] -N≤u，v≤N （10-21）

式中，k为正则化参数。在整个误差范围内，指数响应函数在0与1之间连续地变化。

响应分布搜索区域上的每个点均为“真匹配”的候选者。同时一个点的响应值的高低决定了其成为真匹配的可能性大小。假设两顺序图像帧的时间间隔为1，搜索区域上每一点代表u-v空间中的一个点，那么响应分布可以解释为速度空间中的一个概率分布，即每一点处的响应描述了对应速度值的似然。根据估计理论，利用加权最小二乘方法可得到真实速度的一个估计为

式中，加和是在-N≤u，v≤N上实施的。与此估计相对应的协方差矩阵为

此协方差矩阵特征值的倒数可用作速度估计的置信测度。

对于这种匹配方法，有两个问题值得讨论。第一是有关置信测度概念的引入。在解释响应分布时，默许SSD表面是单峰的。然而对于近似周期性输入，特别是当搜索窗的尺寸大于灰度变化的尺寸时，SSD表面将出现多个局部极小值，上面使用的加权最小二乘方法将“中和”这些峰值，从而产生不正确的速度估计。然而，此时获得的置信测度也是较低的。实际上，置信测度的大小反映了速度估计的可靠程度。可设一个阈值，用逆协方差矩阵的最小特征值作为相应速度估计的置信测度，而后用门限方法提取出“正确”的估计值。尽管这样做会使光流场的密度有所损失，然而却提高了估计精度。第二是有关正则化参数k值的选择。当搜索窗中的响应都很小时，最终的速度估计对k值的选取非常敏感。

3.基于能量的方法(www.xing528.com)

该方法认为光流是基于速度调谐滤波器的输出能量。由于速度调谐滤波器是在傅里叶域中设计的，这类技术也称为基于频率的方法。一个平移二维模式的傅里叶变换为

式中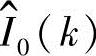，为I（x，y，0）的傅里叶变换；δ为狄拉克函数；w为时间频率；k为空间频率，k=（k_x，k_y）^T。这表明与平移二维模式相关联的所有非零功率均位于通过频率空间原点的一个平面上，这是基于能量方法的一个基本出发点。

在此介绍一下Heeger的方法。他将光流估计公式化为时空能量与频率空间一平面的最小二乘拟合问题。局部能量用Gabor能量滤波器来提取，这些滤波器分属于几个空间尺度，每一尺度有12个滤波器，它们调谐于不同的空间定向和时间频率。理论上，对于单一平移运动，这些滤波器的响应集中在频率空间中一平面附近。对于平移白噪声，Heeger导出了调谐于频率（k_x，k_y，w）的Gabor能量滤波器的预期响应，它是速度的函数，即

式中，σ_x、σ_y、σ_t分别为Gabor滤波器高斯分量的标准偏差。

令E_i为滤波器的预期运动能量，它由式（10-22）给出，不同的i值对应于不同中心频率的滤波器；m_i为测得的运动能量，即相应滤波器的输出；为与第i个滤波器同定向的滤波器族的输出之和；E_i为对应的预测能量之和。使下式最小化可求得（u，v）的一个最小二乘估计：

Heeger提出两条途径来最小化式（10-26），一是用牛顿法实现式（10-26）的非线性最小化，二是采用并行搜索算法。

在基于能量的模型中，首先要对输入图像序列进行时空滤波处理，这是一种时间和空间整合。对于均匀的流场，要获得正确的速度估计，这种时空整合是非常必要的。然而，这样做会降低光流估计的空间和时间分辨率。尤其是当时空整合区域包含几个运动成分（如运动边缘）时，估计精度将会恶化。此外，基于能量的光流技术还存在高计算负载的问题。

4.基于相位的方法

Fleet和Jepson首次从概念上提出了相位信息用于光流计算的问题。因为速度是根据带通滤波器输出的相位特性确定的，因此称为相位方法。他们是根据与带通速度调谐滤波器输出中的等相位轮廓相垂直的瞬时运动来定义分速度的。带通滤波器是按照尺度、速度和定向来分离输入信号的。每一滤波器输出均为复值，表述如下：

R（x，y，t）=ρ（x，y，t）exp（iφ（x，y，t）） （10-27）

式中，ρ和φ分别为滤波器的输出幅值和相位角。于是，垂直于等相位轮廓的速度分量为

V_n=sn （10-28）

速率s和法向单位向量n由下式给出

式中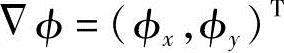，为相位梯度。这实质上是一种微分技术，只不过对象是相位而不是灰度。相位导数可用下式计算：

Fleet和Jepson认为，带通滤波器输出的相位分量比幅值分量更稳定。然而，他们又指出，相位也可能不稳定，不稳定出现在相位奇点的邻域内。可用下列一个对滤波器瞬时频率和幅值变化的约束条件来检测其不稳定性：

式中，（|k|，w）表示滤波器调谐的时空频率；σ_k为各向同性幅值谱的标准偏差；T为一门限，用它来剔除不可靠的分速度测度。此约束条件使相位技术获得了较高的估计精度。

最后，根据来自不同滤波通道的法向速度估计，用一个线性速度模型拟合每个局部区域。在5×5邻域上收集满足稳定性约束的估计值，进而在最小二乘意义下确定最佳的线性速度模型。

基于相位的光流技术的综合性能是比较好的，速度估计比较精确，且具有较高的空间分辨率，对图像序列的适用范围也比较宽。同时，这里仍有几个问题值得讨论：

1）与基于能量的光流技术一样，基于相位的模型既有一定的生物合理性，又有较高的计算复杂性。

2）尽管相位技术用两帧图像就可计算光流，但要获得足够的估计精度，就必须有一定的整合时间，这个延迟将会降低边缘处运动估计的时间分辨率。

3）Fleet和Jepson的方法对输入图像序列中的时间混叠比较敏感。