特征融合的加权主成分分析方法

本系统提出了基于多特征融合的加权主成分分析方法，对于面部表情图像先在表情区划分的基础上提取高维局部自相关（HLAC）特征，再利用加权主成分分析进行降维和特征提取，其中权值的选择除了传统的优化方法，我们采用了基于FACS的快速确定方法。此外，对于面部表情图像识别面临的小样本模式分类问题，本系统尝试用SVM方法进行分类，选用RBF核函数和“一对多”的SVM改进算法。SVM分类器有较强的推广能力，对于小样本训练集分类问题有自身的优势；但受到参数选择和训练速度等影响，应用于动态表情识别时还有一定距离。

1.多特征融合的加权主成分分析

统计特征提取的关键之一就是关于正交基的选取问题，对整体面部图像提取主成分是不是就能最好地表征表情信息，仍然是需要探讨的。这里，为了更好地保留人脸图像中的表情信息，并对其进行有效压缩，我们采用了多特征融合的加权主成分分析方法。

（1）加权主成分分析的提出 第6章中已经介绍过基于K-L变换的主成分分析的基本原理，传统的主成分分析以寻找最小化训练样本的重建误差的变换U（主成分分析的特征向量）为目标：

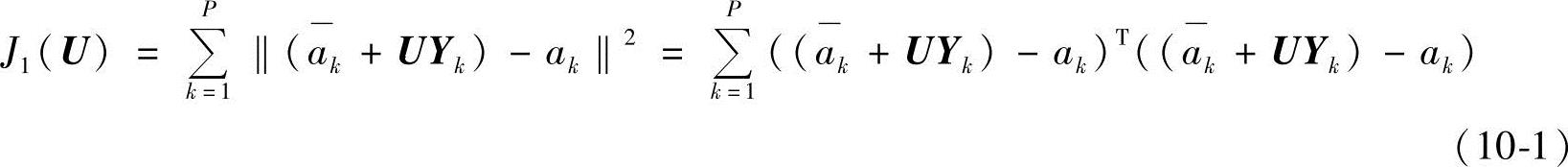
式中，a_k为训练样本；Y_k为训练样本的低维投影；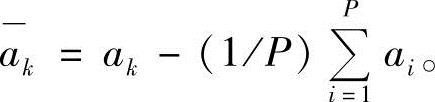

但是，在表情识别中，人脸部件的局部几何形变则起到更为重要的作用。也就是说，面部不同区域在识别过程中起到的作用明显不同，考虑到各维特征在识别中所起的作用不同，可以为每一维特征指定一个系数来代表其重要程度，进而构造样本x_m的加权重建误差计算公式为

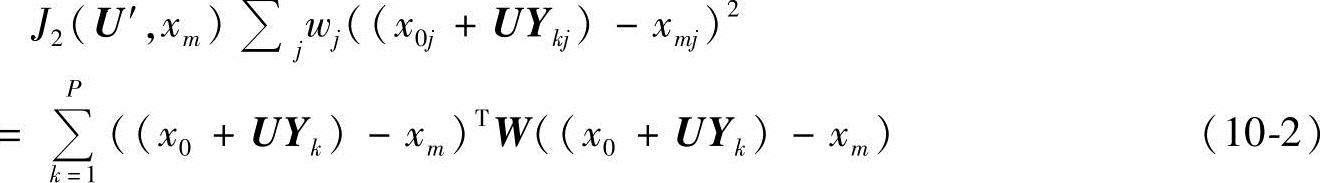
式中，W为权值对角阵，W=Diagonal[w₁，w₂，w₃，…，w_n]，w₁+w₂+w₃+…+w_n=n。

接下来的目标是找到变换矩阵U′，使得所有训练样本的加权重建误差和J₂（U）最小化。

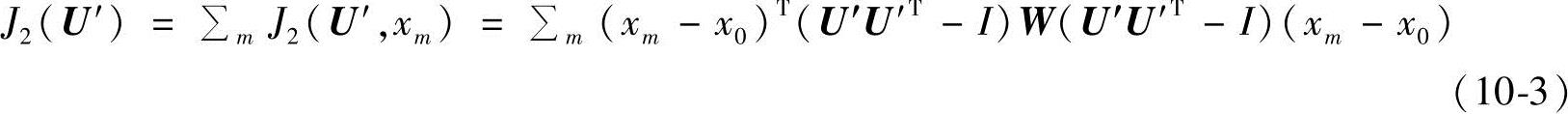
这样，加权主成分分析的基也就是变换矩阵U′的列向量。

当然，可以通过寻优的方法直接计算加权主成分分析的变换矩阵U′，不过这种方法运算比较麻烦，为此在实际中，给出了一个近似算法，对于一定的权值对角阵W，定义其加权协方差矩阵为

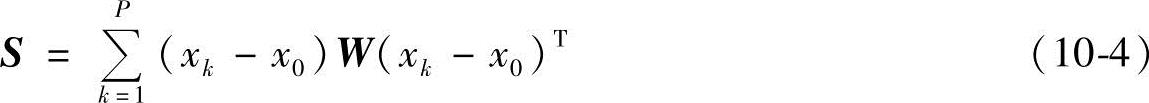
可以使用加权协方差矩阵S的特征向量作为变换矩阵U′。后边的实验也证明这种方法具有很好的效果。

类似于主成分分析，定义U′为加权子空间的基，定义点x到加权子空间U′的距离为

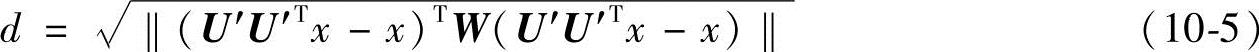
同理，可以依据点x到加权子空间U′的距离进行分类。

（2）权值的确定 我们知道，目前大多数面部分析与识别算法的心理学和生理学依据是Ekman等人在1978年提出的面部动作编码系统（FACS）。该系统源自对面部运动的解剖学的分析，能够测量和记录所有可观察到的面部行。它基于44个独立动作单元（AU）的面部动作，以及一些头部和眼睛的位置和运动。

值得注意的是，FACS只是利用解剖学原理对面部各部位进行测量，还不是对情绪的测量，也就是说，情绪的表示并不是FACS的一部分，它是由一个单独的系统进行编码的。本系统为了进行表情的分析和识别研究，通过FACS解释规则和FACS中的AU组合对各种表情进行建模，也就是将每种表情与AU的线性加权相对应，见表10-1。

表10-1 利用FACS对于基本原型表情的建模

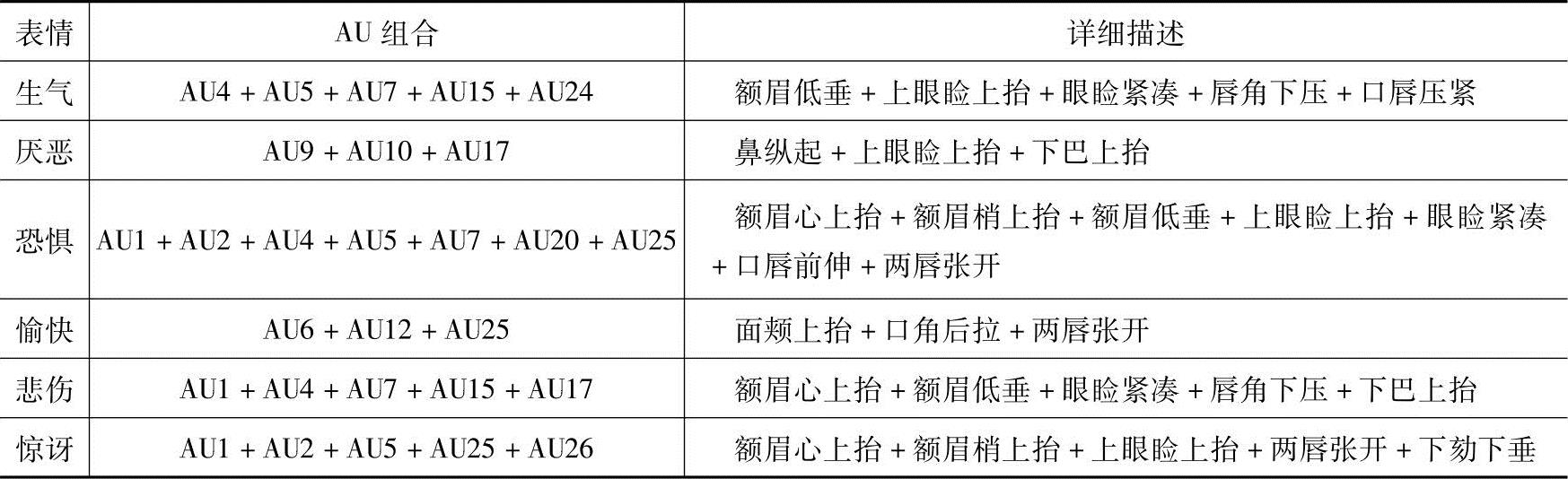
通过表10-1中对不同表情的定义，可以给出一个确定权值的简便算法，即根据组成各类表情的AU在不同选择面部区域的分布来确定。例如对于生气这种表情，包含了5个AU，根据这些AU的组合帮助我们设定眉区、眼区和嘴部区域的权值，经过归一化，依次为0.2、0.4、0.4。

（3）特征融合算法的设计 将特征融合的思想运用于表情识别，要解决的主要问题就是如何有效地融合面部表情的几何特征以及样本学习过程中提取的统计特征。需要特别指出的是，在本节之前，我们已经可以根据前面介绍的基于几何特征的提取方法，有效地进行面部表情区域的提取，并通过计算高维自相关特征，得到各个表情区域的纹理特征，以及通过加权主成分分析提取训练样本的统计特征来进行分类，将这三个步骤有效地结合，就是我们特征融合算法的基本思路。总的来说，算法分为两个部分：训练算法和识别算法。

1）训练算法：

①给定一个面部表情图像集，对每幅图像进行预处理，包括去除孤立的噪声点以及灰度均衡调整。

②利用二阶拉普拉斯算子进行边缘提取、图像二值化，利用对称性改进积分投影方法，确定眉、眼睛和嘴巴的水平坐标，并根据先验知识划分表情区；值得注意的是，此时原始训练样本的维数（图像的像素数）已经下降为表情区的维数。

③对三个不同表情区分别计算高维自相关特征，并将其作为下一步训练的样本。

④对三个不同表情区的自相关特征进行加权的K-L变换，得到由前m个特征向量组成的加权变换矩阵。

⑤将训练样本集中的每一幅图像进行表情区分割和高维自相关特征提取，通过加权变换矩阵映射到表情空间，并求出每一类面部表情图像在表情空间的聚类中心。

2）识别算法：

①对未知面部表情图像进行预处理，去除孤立的噪声点以及灰度均衡调整。

②利用边缘提取、图像二值化和对称性改进积分投影方法，确定眉、眼睛和嘴巴三个表情区。

③对三个不同的表情区分别计算高维自相关特征，并通过加权变换矩阵将其映射到表情空间。

④计算新的图像（表情空间中的一个点）到表情空间中各个聚类中心的距离，并根据近邻中心（Nearest Center）分类器进行归类。

2.支持向量机表情分类

具体地说，利用支持向量机算法进行表情分类需要考虑以下三个方面的问题。(www.xing528.com)

（1）确定多类别支持向量机分类方法 利用支持向量机（SVM）算法进行表情识别，首先要确定如何将两类别分类方法扩展到多类别分类方法。假定多类别分类问题有k个类别S={1，2，…，k}，训练样本为{（x_i，y_i），i=1，2，…，l}，其中y_i∈S。主要有以下三种方法可实现SVM的多类别分类：一对多分类器、一对一分类器和决策树分类器。这三种方法在第7章7.2节中曾经介绍过。本系统采用的是一对多分类器。它是用来构造k个SVM子分类器的。在构造第j个SVM子分类器时，将属于第j类别的样本数据标记为正类，不属于j类别的样本数据标记为负类。测试时，对测试数据分别计算各个子分类器的判别函数值，并选取判别函数值最大所对应的类别为测试数据的类别。

本系统将支持向量机和最近邻准则相结合作为表情识别的分类器。设有七类面部表情样本（平静、高兴、悲伤、厌恶、恐惧、惊奇、生气），每类样本都有一个对应的SVM分类器，将其与其他表情分开。经训练所得的七个SVM可以将面部表情样本分为七类。当输入一个新的测试样本时，该测试样本由七个SVM进行分类，会出现三种情况：其一，第i个SVM将测试样本判为第i类，即输出为1，其余的SVM输出为-1，则判断该样本属于面部表情库中的第i类表情；其二，多个SVM同时输出为1，此时应用最近邻准则来判断类别，即计算这些SVM对应的表情样本与测试样本的欧氏距离D=||x-y||²，将测试样本判为与其距离最近的面部表情样本；其三，所有SVM将测试样本判为-1，则判断该测试样本的类别不属于表情训练样本库中类别。

（2）核函数选择 在采用支持向量机对面部表情进行分类时，首先必须对SVM进行模型选择，即首先确定核函数类型。

这里，选择RBF核函数，其表达式为K（x_i，x_j）=exp（-γ||x_i-x_j||²），γ＞0，主要原因有：

1）RBF核函数可以把低维特征空间映射到高维特征空间，通过引入惩罚项解决线性不可分问题，而线性核函数主要是针对线性可分问题，而且带惩罚项的线性核函数是RBF核函数的一种特例。另外，Sigmoid核函数表现出的性能也和带有特定参数（C，γ）的RBF核函数性能等价。

2）核函数参数个数也对SVM模型选择的复杂性带来影响，在这一点上，选择RBF核函数（只有一个参数γ）显然要比选择多项式核函数更方便。

3）选择RBF核函数给数字处理也将带来一定的方便。我们知道，RBF核函数是高斯函数，它的取值范围为（0，1），对于多项式核，当多项式的阶次比较大时，其取值有可能趋向无穷大[（γx^T_ix_j+r）＞1时]或零[（γx^T_ix_j+r）＜1时]，而Sigmoid核函数，只是在特定条件下才满足Mercer条件。

（3）模型参数C和γ的选择 关于SVM的研究表明，特征空间的维数与SVM的复杂度没有直接关系，核参数影响数据在特征空间分布的复杂程度，误差惩罚参数C通过调整给定特征空间中经验误差的水平来影响学习机器推广能力。参数C和γ的影响是同时存在的，只有综合考虑才能得到性能最优的SVM。因此确定了RBF核函数后，必须对两个未知参数C和γ进行选择，使得对任意的未知面部表情图像，SVM能做出准确分类。其中，误差惩罚参数C的作用是在确定的数据子空间中，调节学习机器置信范围和经验风险的比例，以使学习机器的推广能力最好。不同数据子空间中最优的C是不同的。在确定的数据子空间中，C的取值小表示对经验误差的惩罚小，学习机器的复杂度小而经验风险值较大；反之亦然。前者称为“欠学习”现象，而后者则称为“过学习”。每个数据子空间至少存在一个合适的C使得SVM推广能力最好。当C超过一定值时，SVM的复杂度达到了数据子空间允许的最大值，此时经验风险和推广能力几乎不再变化。

由统计学习理论可以知道，在训练分类器时，不能一味地追求经验风险最小（即训练误差最小），那样势必造成分类器过训练，使得分类器推广误差比较差。因此，在训练分类器时，可以采用交叉验证（Cross-validation）的方法，把训练样本集分成互不相交的两部分：其一为常规的训练集，用于调整SVM参数；其二为验证集（Valitation Set），用于评价SVM的推广误差。实际上，常常首先给出（C，γ）一个大概的取值范围，对其中的每一对（C，γ）取值，再分别采用交叉验证方法进行训练SVM，这样可得到一组较优参数值。

3.算法的程序实现

这里主要解决两个方面的问题：一是算法的速度改进问题；二是如何利用程序来实现相关算法。

（1）算法的速度改进 系统实现需要设计的算法包括通过人脸图像预处理、表情区分割、加权主成分特征提取和表情分类等算法。原有的一些算法需要较长的执行时间，运行效率低，因此有必要对原有算法进行改进，使之更适应视频图像处理的特点。

1）利用“三庭五眼”缩小积分投影的搜索范围：在实际运用中，为了提高特征提取的速度，还可以利用人脸结构特点的先验知识缩小积分投影范围。所谓人脸结构特点是指，人脸各个部分虽然没有绝对的标准，并在一定范围内变化，但它们之间有一定的比例关系，即通常所说的“三庭五眼”（参见第2章），这些先验知识给人脸图像中眼睛特征的定位提供了依据，可以据此确定在人脸图像的中间三分之一的矩形区域内（即“三庭”中的“眉毛到鼻孔”间）搜索水平灰度投影的谷值，得到眼睛的水平位置的确定值。这样不仅可以减少噪声的影响，也可以在一定程度上减少计算量。

由前面定位眼睛的方法和所得的灰度水平积分投影图可知，对面部表情图像进行水平灰度投影，通过对投影曲线的分析同样可以确定人脸图像中的嘴也对应水平积分投影曲线的谷值区域，由此可以粗略地检测出嘴的位置。这里，由先验知识知道两嘴角的位置大概位于眼睛瞳孔的下方，因此如果在长为两眼睛瞳孔的下方距离、宽为下巴以上1/3人脸距离的矩形区域计算水平投影的值，就可以根据其谷值比较准确地确定嘴的水平位置。

2）求取变换矩阵的快速算法：人们知道C是一个d×d的矩阵，其中d是训练图像的像素数，例如取256×256像素的训练图像，d的值就高达65536！因此求高维矩阵C的特征值和特征向量是计算量非常大的。这里通过矩阵的变换，得到快速的算法。

C=AA^T

式中

矩阵AA^T的特征值λ_l和特征向量u_l满足：AA^Tu_l=λ_lu_l，l=1，2，…，d。

一般来说，训练过程中，面部表情图像的样本数不会高于图像的像素数d，所以可以先求A^TA的特征向量u_l′：

A^TAu_l′=λ_lu_l′ （10-7）

将等式两边同时左乘矩阵A，得AA^TAu_l′=Aλ_lu_l′=λ_lAu_l′，因此得到

u_l=Au_l′ （10-8）

这样求高维矩阵C=AA^T的特征值和特征向量的问题就转化为：先求较低维的矩阵A^TA的特征值和特征向量，在将其特征向量左乘矩阵A，这样大大减小了计算量，所以称为求取变换矩阵U的快速算法。

（2）算法的程序实现 用多特征融合的加权主成分分析方法进行表情识别，在编程过程中一个重点就是求实矩阵的特征值和特征向量的问题，这里我们学习了计算方法中的相关知识，由于协方差矩阵为对称矩阵，所以先用豪斯霍尔德（Householder）矩阵把实对称矩阵变形到对称三角矩阵，并可积累变换矩阵。然后利用隐式QL算法，确定一个实对称三角矩阵的特征值和特征向量，此算法运行时间较短，占用内存较少，舍入误差也小。由于本书篇幅有限，这里对算法的具体实现过程不做详细的介绍，可以参见程序中TRED（）和TQLI（）两个函数。

1）TRED（A[]，N[]，D[]，E[]）使用说明

N：整型变量，输入参数，实对称矩阵的阶数；

A[]：N×N个元素的二维实型数组，输入、输出参数，输入时存放实对称矩阵A，输出时存放积累的正交变换矩阵Q；

D[]：N个元素的一维实型数祖，输出参数，存放变形后的三角对称矩阵的对角线元素；

E[]：N个元素的一维实型数祖，输出参数，存放变形后的三角对称矩阵的非对角线元素，其中E[1]=0；

2）TQLI（D[]，E[]，N，Z[]）使用说明

N：整型变量，输入参数，矩阵的阶数；

D[]：N个元素的一维实型数祖，输入、输出参数，输入时存放对称三角矩阵的对角元素，输出时存放矩阵的特征值；

E[]：N个元素的一维实型数祖，输出参数，存放对称三角对称矩阵的非对角线元素，其中E[1]=0；

Z[]：N×N个元素的二维实型数组，输入、输出参数，如果是求三角对称矩阵的特征向量，则输入为单位矩阵，若是求由一般对称矩阵变形到三角对称矩阵的一般对称矩阵的特征向量，则输入前面的TRED的输出矩阵A，输出时其第K列存放对应于特征值D（K）的规范化特征向量。