FAP驱动技术：实现人脸动画的原理解析

根据FAP控制人脸运动类型的不同，66个普通FAP分为两类：第一类控制人脸某些区域的旋转、平移和缩放等的简单变换，该区域点的运动具有简单的统一规则，比如转动眼珠；第二类控制人脸某些区域的非简单变换，区域点的运动没有简单的统一规则，比如皱眉、眨眼、张嘴等。用户在得到一组FAP的值后，需要用到FDP域中的人脸动画定义表来控制人脸网格的变形，而得到相应的表情。

对于第一类FAP，人脸动画定义表中定义了FAP的运动类型，包括旋转、缩放和平移三种。如果运动类型是旋转的话，还需要定义旋转轴和旋转因子，如果运动类型是缩放和平移的话，只需要定义三维比例因子就可以了。

对于第二类FAP，人脸动画定义表中定义了三部分内容：①FAP的值域分为哪几段；②FAP控制哪些网格点；③FAP控制的网格点在每段中的运动因子是多少。对于每一个FAP，需要在人脸动画定义表中查找出这三部分内容，然后根据MPEG-4中提供的算法，计算出由该FAP控制的所有网格点的位移。对于一组FAP，每个FAP都计算出影响网格点位移的大小，将这些位移叠加起来就可以得到一个生动的人脸表情。

根据给定的FAP值，对于某一特定的三维人脸网格，实现FAP值指定的人脸表情，是基于MPEG4的三维人脸实现过程中需要考虑的关键问题。

第一类FAP比较简单，用来度量的FAPU也只有AU。举例来说，对于FAP23（水平旋转左眼珠），已知AU=10^-5，定义旋转轴为（0，-1，0），旋转因子θ=1，如果FAP23的大小为10000，那么左眼珠逆时针旋转的角度α=10^-5×10000×1rad=0.1rad。

第二类FAP计算网格点坐标则相对比较复杂，相应地，AU也有IRISD、ES、ENS、MNS、MW五个。这一类FAP控制区域点的形变，用若干段线性形变来代替。在同一段中，点的位移是在固定方向匀速变化的。例如，FAP19控制左眼上眼皮的运动。眨眼时，眼皮实际上是在做弧线运动，可以把它近似为两段直线运动，如图8-11所示。控制区域内的所有点在每一段都分别有一个三维的运动因子，描述该点在本段中在三个坐标轴方向上的运动快慢。

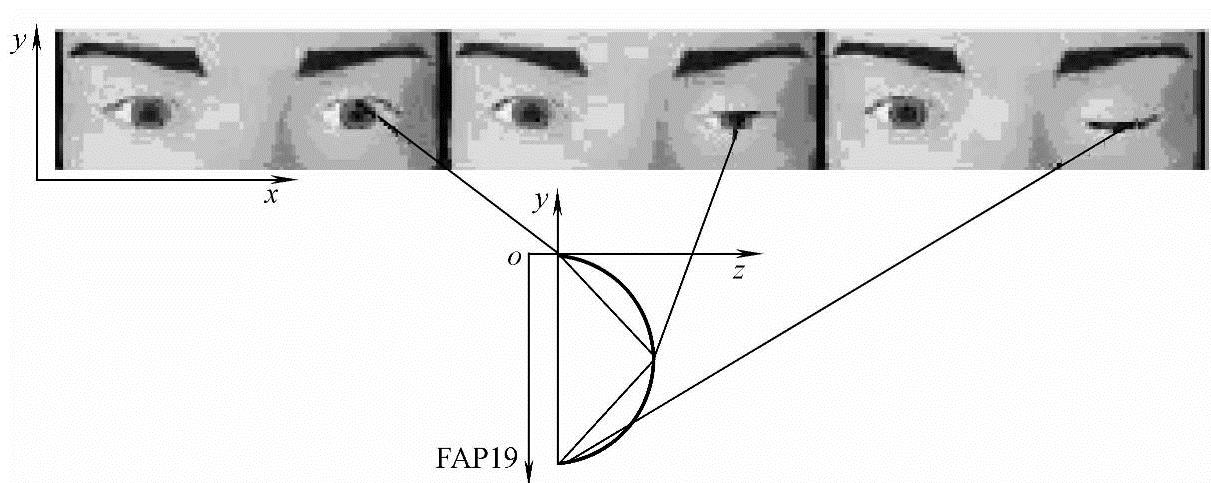
图8-11 左眼上眼皮运动的两个阶段

对于第二类FAP，MPEG-4给出了一个计算该FAP控制区域内点的位移的算法。该算法如下：

假设P_m是FAP控制区内m点在中性表情（FAP=0）下的空间坐标，P_m′是m点根据FAP值改变位置后的空间坐标，D_m，k是m点在第k段的三维运动因子，那么可以按下面的步骤计算P_m′的值。

1）设FAP值域共分为max+1段，分别为[I₀，I₁]、[I₁，I₂]、[I₂，I₃]，…，[I_max，I_max+1]，其中I₀=-∞，I_max+1=+∞。设FAP值在[I_j，I_j+1]段，0在[I_k，I_k+1]段，0≤j、k≤max。如果FAP或0正好在边界点上，那么可以任选边界点前后的区域作为FAP或0所在的段。

2）如果j＞k，那么可以用下式计算P_m′的值：(www.xing528.com)

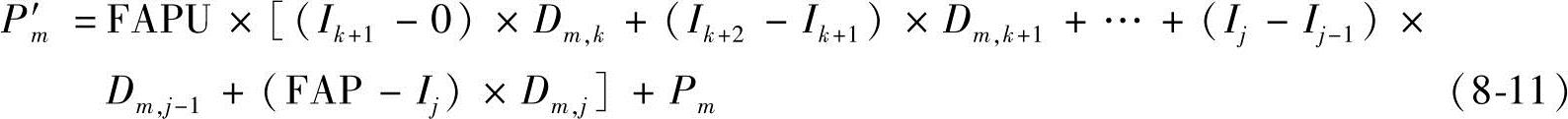
3）如果j＜k，那么可以用下式计算P_m′的值

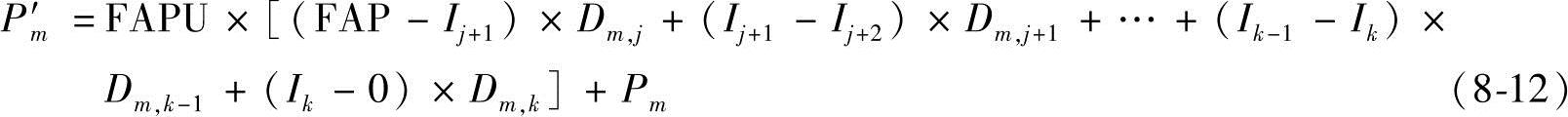
4）如果j=k，那么可以用下式计算P_m′的值：

P_m′=FAPU×FAP×D_m，j+P_m （8-13）

5）如果FAP只分了1段，也就是说点是严格线性运动的，那么也可以用式（8-13）来计算P_m′的值。

下面举一个具体实例。假设某FAP的运动分了三段，分别为：[-∞，0]，[0，500]，[500，+∞]，受该FAP控制的点m在三段中的运动因子分别为（1 0 0），（0.9 0 0），（1.5 0 4），m点在中性表情下的坐标为P_m，如果给出FAP的值为600，对应的FAPU是0.1。由于FAP的值在[500，+∞]区间，即第2段，而0在[0，500]区间，即第1段，所以应该用式（8-12）计算，那么m点新的坐标就应该是

P_m′=0.1×[（500-0）×（0.9 0 0）T+（600-500）×（1.5 0 4）T]+P_m

=（60 0 40）T+P_m

可以看到，这个算法把复杂的脸部肌肉运动近似成分段的线性运动。要求解未知数P_m′，只需要解一个一元一次线性方程，求解速度非常快，完全可以满足实时运算的要求。另外，线性运动分段的多少决定着与实际运动的近似程度，分段多固然可以提高运动的逼真度，但是要计算分段点，以及每段各点的运动因子也涉及很多工作，所以可以根据实际应用的需要来确定分段的多少。