纹理映射的参数曲面及逆映射

简单地说，纹理分为两种：一种是通过颜色色彩或明暗的变化体现出表面细节，这种纹理称为颜色纹理；另一种纹理则是由于不规则的细小凹凸造成的，例如橘子皮的皱纹或未磨光的凹痕等。纹理映射技术有连续法和离散法两种，连续法把纹理定义为一个二元函数，函数的定义域就是纹理空间。离散法把纹理函数定义在一个二维数组中，代表纹理空间中行间隔和列间隔固定的一组网格点上的纹理值。通过对网格点的值进行插值获得网格点之间的其他点的纹理值。

当前的纹理生成方法有三大类：

（1）无纹理生成法 这种方法没有纹理，一般是通过光照给模型外表涂上颜色，优点是简单快速，缺点是人物缺乏真实感。由于没有纹理的视觉干扰，通常在准确表现模型三维几何形状时会采用这种方法。

（2）单张纹理生成法 在人脸动画中，只使用一张中性表情的纹理，在动画显示过程中，纹理随着网格的变形而做相应的拉伸。单张纹理的优点是纹理控制简单，只需要把纹理映射到网格上，在动画中随着网格的变形而拉伸。缺点是不能表现纹理的细微变化，人脸面部的纹理随着表情的改变会产生细微的变化，比如皮肤褶皱等，只用一张纹理无法表现这些细微的变化，在真实度上会有所欠缺。根据纹理的获取途径不同，单张纹理生成法又可以分为以下三类：

1）照片图像拼接法：最常见的方法是用一张正面的照片和一张侧面的照片来拼接组成一张纹理，也有用多张不同角度照片拼接的纹理。这种方法的关键是要做到不同照片上同一特征点的标定要准确。照片拼接的方法简单易行，生成的纹理在正面通常都会有很好的效果，主要缺点是不同照片上的相同特征点很难准确对应，生成的纹理在偏离正面角度较大的情况下效果不很理想。

2）视频图像拼接法：通过跟踪视频中人脸的特征位置和姿态来获取不同角度的人脸纹理，然后把各种角度的纹理融合起来合成一张完整的纹理。该方法主要适用于只有视频的条件下生成纹理的情况，产生效果与照片图像拼接类似。

3）三维扫描设备法：用三维扫描仪自动扫描拼接生成纹理，纹理结果准确，但是常会有一些空白区域，需要用插值算法进行修补。三维扫描的方法需要模特的配合，难以推广。

（3）变化纹理生成法 为了表现人脸面部细微特征的变化，变化纹理的方法在动画过程中并不局限于一张固定的纹理，而是随着表情的变化对纹理进行相应的修改。变化纹理生成法真实感强，但是相对于单张纹理生成法，实现起来比较复杂。目前已有的变化纹理生成法有：

1）动态重构法：Guenter等人在模特脸上标了6种不同颜色，共128个点，用6架照相机同时采集人脸表情。然后用一个颜色分类器来识别不同颜色，并获得它们的位置，利用这些点在不同视角的坐标，可以重构三维人脸网格。为了获取纹理，他们首先根据颜色分类器的信息，把照片上的彩色点去掉，并用正确的颜色来填充，然后拼接融合6张照片生成不含标定点的纹理。由于纹理总是用真实的表情照片生成的，而不是靠拉伸得到的，因此可获得生动的动画效果，但是他们的动画只适应于特定人模型，且制作过程复杂，无法实时产生动画。(www.xing528.com)

2）纹理拼接法：Pigbin等人采用5架相机采集模特的各种基本表情，他们把人脸分成很多区域，然后用各个区域的纹理进行拼接，从而产生该模特更多丰富的表情。由于建立了真实的表情纹理库，所以生成的纹理效果很逼真，具备各种细微特征。但是他们的工作只适应于特定人模型，而且制作过程复杂，通用性不强。

生成颜色纹理的一般方法是在一个平面区域（即纹理空间）上，预先定义纹理图案，然后建立物体表面的点与纹理空间的点之间的对应（即映射）。当物体表面的可见点确定之后，以纹理空间的对应点的值乘以亮度值，就可以把纹理图案附到物体的表面上。也可以用类似的方法给物体表面产生凹凸不平的包纹理，不过这时纹理值作用在法线向量上，而不是作用于颜色亮度上。纹理贴图到物体表面是通过纹理空间与物体空间之间的坐标变换来实现的。二维纹理映射是从二维纹理平面到三维景物表面的一个映射。图像纹理映射确定景物表面上任一可见点P在纹理空间中的对应位置（u，v），（u，v）所定义的纹理值或颜色值描述了景物表面在P点处的表面颜色纹理属性。图像纹理映射技术要建立纹理空间与景物空间之间的映射m和景物空间与屏幕空间之间的映射T，由于景物空间与屏幕空间之间的映射T是取景变换，所以关键是确定纹理空间与景物空间之间的映射m。纹理映射的过程如图8-4所示。

映射m可描述为（u，v）=f（x，y，z），（u，v）和（x，y，z）分别为纹理空间和物体空间中的点。图像纹理平面区域一般经过归一化处理，定义在单位正方形域（0≤u≤1，0≤v≤1）上，便于后续计算。

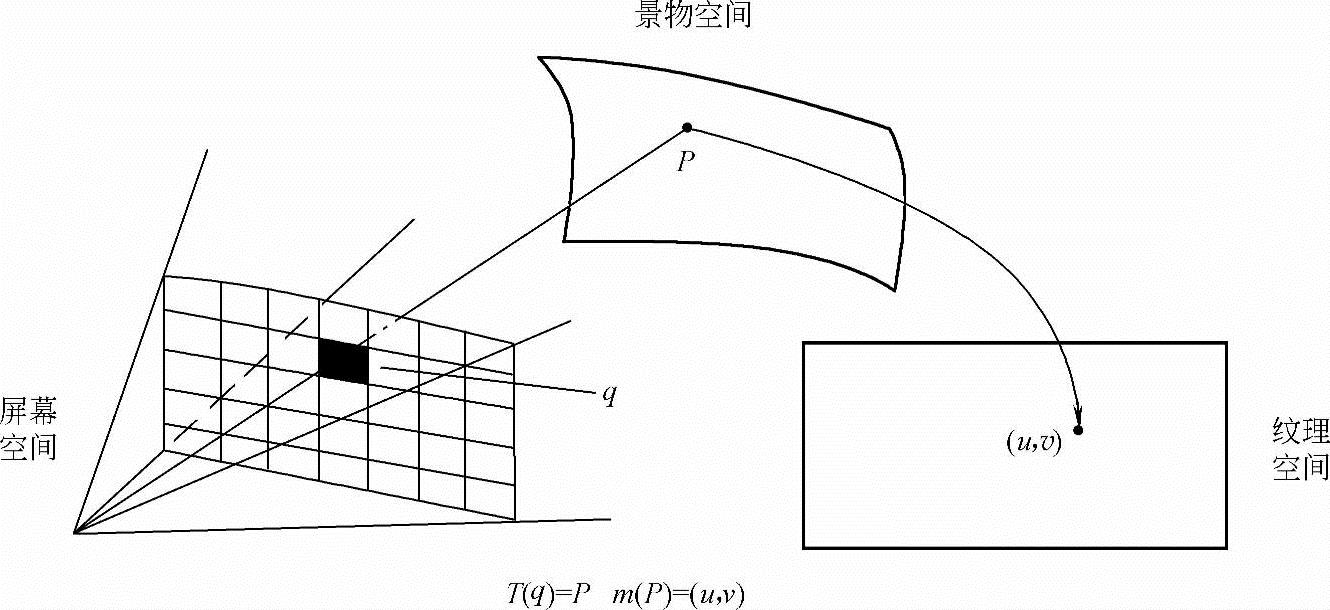
图8-4 纹理映射过程示意图

由于参数曲面定义了一个二维参数空间到三维参数空间的映射关系，当将参数空间和纹理空间等同起来看时（两者之间关系由一仿射变换确定），映射m等价于参数曲面自身定义的逆映射。对于一般三角形或四边形，空间点坐标与参数的关系为仿射变换，即

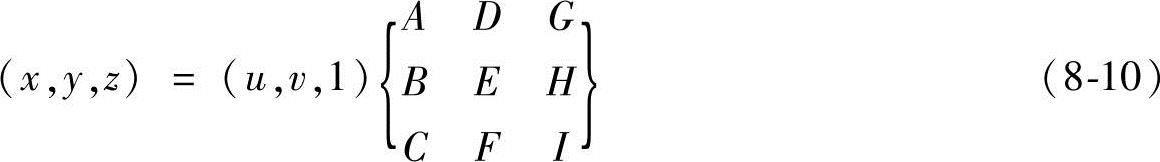
指定三个顶点的（u，v）值，可算出系数矩阵中各系数的值。式（8-10）定义了纹理空间与多边形平面之间的一个通用仿射变换。对复杂的高次参数曲面来说，其逆映射无法解析表达，一般需采用数值求解技术来离散求得。对简单的二次曲面来说，其纹理映射可解析地表达出来。