模糊数学的基本理论解析

1.模糊子集

（1）模糊子集的定义 设给定论域U，U到[0，1]闭区间的任一映射μR

都可确定U的一个模糊子集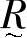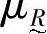，称为模糊子集的隶属函数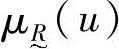，称为u对于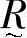的隶属度。隶属度也可记为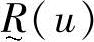。在不混淆的情况下，模糊子集也称为模糊集合。

上述定义表明，论域U上的模糊子集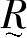由隶属函数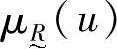来表征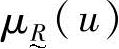，取值范围为闭区间[0，1]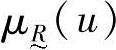，的大小反映了u对于模糊子集的从属程度。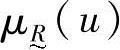的值接近于1，表示u从属于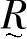的程度很高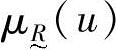；的值接近于0，表示u从属于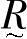的程度很低。可见，模糊子集完全由隶属函数来描述。

（2）模糊集合的表达方式 当U为有限集{u₁，u₂，…，u_n}时，通常有如下三种模糊集合的表达方式：

1）Zadeh表示法：

式中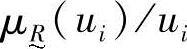，并不表示“分数”，而是表示论域中的元素u_i与其隶属度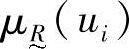之间的对应关系。“+”也不表示“求和”，而是表示模糊集合在论域U上的整体。

2）序偶表示法：将论域中的元素u_i与其隶属度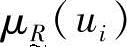构成序偶来表示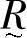，则

此种方法隶属度为0的项可以不写入。

3）向量表示法：

在向量表示法中，不能省略隶属度为0的项。

2.模糊关系

模糊关系的定义 在普通集合论中，设U、V是两个论域，称

U×V={（x，y）|x∈U，y∈V} （7-186）

为U、V的直积或笛卡儿积。

从U到V的一个关系定义为集合U、V的直积U×V的一个子集R，记作

推广到模糊子集，有：

【定义7-3】 直积U×V的一个模糊子集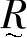的就是U到V的模糊关系。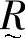的隶属函数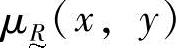表示了U中的元素x与V中的元素y具有关系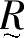的程度。

模糊关系完全由其隶属函数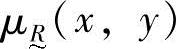来刻画，当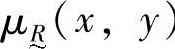为1或0两个极端值时，模糊关系即变为经典关系。(www.xing528.com)

对于有限论域U=（x₁，x₂，…，x_m），V=（y₁，y₂，…，y_m），U对V的模糊关系可用矩阵R=（r_ij）m×n来表示，其中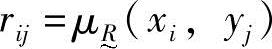。矩阵R=（r_ij）_m×n称为模糊矩阵。模糊关系的运算完全可以通过模糊矩阵来进行。

3.隶属函数的确定

隶属函数是对模糊概念的定量描述。隶属度和隶属函数是模糊数学中的两个重要概念，对模糊数学的应用，几乎都与这两个概念联系在一起。

例如我们说“小王性格稳重”，性格稳重就是一个模糊概念。人们在头脑中区别这个概念时，并不要作绝对的肯定或者否定，所要求的只是小王对“性格稳重”这个概念符合到什么样的程度，这个程度可用[0，1]上的一个实数去度量，这个实数便是“隶属度”。如果它随着变量x的改变而改变，那么这个从变量到隶属度的映射关系就是“隶属函数”，它可以用客观的方法确定，也可以凭经验判断得出。例如，按某种原则确定小王的性格稳重程度为0.8，即小王（记作a）对于“性格稳重”的隶属函数A（x），当x=a时的值为0.8，记作A（a）=0.8。

（1）确定隶属函数的原则 隶属函数的确定过程本质上说应该是客观的，但每个人对于同一个模糊概念的认识理解又有差异，因此隶属函数的确定又带有主观性。它的建立应遵循下述原则：

● 隶属函数的建立虽有主观性、但不能有随意性。

● 建立隶属函数之前，须对于待确定的模糊概念相关的客观因素进行充分的考察，以取得可靠的数据。

● 参与建立隶属函数的人员，不仅要对待确定的模糊概念有主观上的充分认识，同对也必须有将其认识转化为数学表示的能力。

● 可根据具体问题的特点，同时试用几种建立隶属函数的方法分别建立相应的隶属函数，然后再从中选取一种更为合适的隶属函数。

● 隶属函数建立后，使用过程中根据具体情况再做某些调整。

● 对于清晰的情况，相应的隶属度值只能取0或1，绝不能将清晰概念模糊化。

（2）隶属函数的确定 确定隶属函数的方法有很多种，目前常用的确定方法有模糊统计法、专家经验法（又叫Delphi法）、对比法和因素加权统计法等。在此就不一一详细介绍了，具体内容请参考模糊数学方面的书籍。根据处理对象的不同，要选取不同的方法。选取方法有以下几个原则：

1）若模糊集反映的是社会的一般意识，它是大量的可重复表达的个别意识的平均结果，例如青年人、经济增长快、生长正常等，则此时采用模糊统计法来求隶属函数较为理想。

2）如果模糊集反映的是某个时间段内的个别意识、经验和判断，例如，某专家对某个项目可行性的评价，那么对这类问题可以采用Delphi法。

3）若模糊集反映的模糊概念已有相应成熟的指标，这种指标经过长期实践检验已成为公认的对事物的真实的又是本质的描述，则可直接采用这种指标，或者通过某种方式将这种指标转化为隶属函数。

4）对某些模糊概念，虽然直接给出其隶属函数比较困难，但却可以比较两个元素相应的隶属度，此时可用相对选择法求得隶属函数。

5）若一个模糊概念是由若干个模糊因素复合而成的，则可先求各因素模糊集的隶属函数，再综合出模糊概念的隶属函数。

需要特别指出的是，隶属函数应通过实践检验，利用信息反馈，不断进行调整，使隶属函数的形成成为一种学习的过程，以求达到相对稳定的状态。