人工神经元模型及其应用

人工神经网络（ANN）是由大量处理单元（人工神经元、处理元件、电子元件、光电元件等）经广泛互连而组成的人工网络，用来模拟脑神经系统的结构和功能。它是在现代神经科学研究的基础上提出来的，反映了人脑功能的基本特性。在人工神经网络中，信息的处理是由神经元之间的相互作用来实现的，知识与信息的存储表现为网络元件互连间分布式的物理联系，网络的学习和识别取决于各神经元连接权值的动态演化过程。

1.人工神经元

正如生物神经元是生物神经网络的基本处理单元一样，人工神经元（简称为神经元）是组成人工神经网络的基本处理单元。在构造人工神经网络时，首先应该考虑的问题是如何构造神经元。在对生物神经元的结构、特性进行深入研究的基础上，心理学家麦克洛奇（W.McCulloch）和数理逻辑学家皮兹（W.Pitts）于1943年首先提出了一个简化的神经元模型，称为M-P模型。图7-16所示为一个基本的人工神经元的结构。

图7-16 人工神经元模型

人工神经元又称为处理单元、节点或短期记忆。从外部环境或别的神经元的输出构成输入向量（x₁，x₂，…，x_n）^T，其中x_i为别的神经元的输出或兴奋水平。连接两个神经元的可调值称之为权值或长期记忆。所有和神经元j相连接的权值构成向量W_j=（w_j1，w_j2，…，w_jn）^T，其中w_ji代表处理单元i和j之间的连接权值。通常还加上一个域值常数θ_j。此时神经单元的计算过程可以表示为

y_j=f（W_j^Tx-θ_j） （7-161）

或者写成

通常取下列函数之一：

（1）线性函数

f（x）=α·x （7-163）

（2）带限的线性函数

式中，γ为神经元的最大输出值。

（3）域值型函数

式中，θ为神经元阈值。

（4）最为常用的Sigmoid函数

与此类似的还有双曲函数

人工神经网络是由神经元广泛互连构成的，不同的连接方式就构成了网络的不同连接模型，常用的有以下几种：

● 前向网络：前向网络又称为前馈网络。在这种网络中，神经元分层排列，分别组成输入层、中间层（又称隐层。可有多层）和输出层。每一层神经元只接收来自前一层神经元的输入。输入信息经各层变换后，最终在输出层输出。

● 反馈网络：即从输出层到输入层有反馈，这种网络与上一种网络的区别仅仅在于，输出层上的某些输出信息又作为输入信息送入到输入层的神经元上。

● 层内有互连的网络：在前面两种网络中，同一层上的神经元都是相互独立的，不发生横向联系。而在这一种网络中，同一层上的神经元可以互相作用。这样安排的好处是，可以限制每层内能同时动作的神经元数，亦即可以把每层内的神经元分为若干组，让每组作为一个整体来动作。例如，可以利用同层内神经元间横向抑制的机制把层内具有最大输出的神经元挑选出来，从而使其他神经元处于无输出的状态。

● 互连网络：在这种网络中，任意两个神经元之间都可以有连接。在无反馈的前向网络中，信息一旦通过某个神经元，过程就结束了，而在该网络中，信息可以在神经元之间反复往返地传递，网络一直处在一种改变状态的动态变化之中。从某初态开始，经过若干次的变比，才会达到某种平衡状态，根据网络的结构及神经元的特性，有时还有可能进入周期振荡或其他状态。

2.人工神经网络的特征及分类

（1）人工神经网络的主要特征

1）能较好地模拟人的形象思维。逻辑思维与形象思维是人类思维中两种最重要的思维方式，人工神经网络是对人脑神经系统结构及功能的模拟，以信息分布与并行处理为其主要特色，因而可以实现对形象思维的模拟。

2）具有大规模并行协同处理能力。在人工神经网络中，每一个神经元的功能和结构都是很简单的，但由于神经元的数量巨大，而且神经元之间可以并行、协同地工作，进行集体计算，这就在整体上使网络具有很强的处理能力。另外，由于神经元通常都很简单，这就为大规模集成的实现提供了方便。

3）具有较强的容错能力和联想能力。在人工神经网络中，任何一个神经元及任何一个连接对网络整体功能的影响都是十分微小的，网络的行为取决于多个神经元协同行动的结果，其可靠性来自这些神经元统计行为的稳定性，具有统计规律性。因此，当少量神经元或它们的连接发生故障时，对网络功能的影响是很微小的，这正如人脑中经常有脑细胞死亡，但并未影响人脑的记忆、思维等功能一样。神经网络的这一特性使得网络在整体上具有较强的鲁棒性（硬件的容错性）。另外，在神经网络中，信息的存储与处理（计算）是合二为一的，即信息的存储体现在神经元互连的分布上。这种分布式的存储，不仅在某一部分受到损坏时不会使信息遭到破坏，得以尽快恢复，增强网络的容错性，而且能使网络对带有噪声或缺损的输入有较强的适应能力，增强网络的联想及全息记忆能力。

4）具有较强的学习能力。它能根据外界环境的变化修改自己的行为，并且能依据一定的学习算法自动地从训练实例中学习。它的学习主要有两种方式，即有教师的学习与无教师的学习。所谓有教师的学习是指，由环境向网络提供一组样例，每一个样例包括输入及标准输出两部分，如果网络对输入的响应不一致，则通过调节连接权值使之逐步接近样例的标准输出，直到它们的误差小于某个预先指定的阈值为止。所谓无教师的学习是指，事先不给出标准样例，直接将网络置于环境之中。学习阶段与工作阶段融为一体，这种边学习边工作的特征与人的学习过程相类似。

（2）人工神经网络的分类 迄今为止，已经开发出了几十种神经网络模型，从不同角度进行划分，可以得到不同的分类结果：

1）若按网络的拓扑结构划分，则可分为无反馈网络与有反馈网络。

2）若按网络的学习方法划分，则可分为有教师的学习网络与无教师的学习网络。

3）若按网络的性能划分，则既可以分为连续型与离散型网络，又可分为确定型与随机型网络。

4）若按连接突触的性质划分，则可分为一阶线性关联网络与高阶非线性关联网络。

（3）人工神经网络的学习 人工神经网络的学习分为有监督学习和无监督学习。有监督学习，是指在学习时，有一个内在的或外在的“教师”，具有更高的动机和指挥的自矫正学习。无监督学习，则是对所有实时和短时的感知器输入进行预处理，这种预处理是无心（Without Conscience）的，并且有关联记忆（Associative Recall）。这两种学习在人脑中是并行进行的，不像传统的人工神经网络是在不同的结构上独立进行的。

1）有监督学习人工神经网络：有监督学习神经元j的输入为（x₁，x₂，…，x_n），与输出神经元j的权为（w_j1，w_j2，…，w_jn），它的模型如图7-17所示，通过学习使输出与要求的值t_j相等。

在多层神经网络中，如非线性输入、输出关系取y_j=sign（u_i）时，则为感知器模型；如输入、输出关系取单调上升函数时，为反向传播BP网络。它们都是前馈式神经网络，有时还称为“概率型神经网络”（PNN）。如采用反馈式神经网络结构，在每个神经元之间都有连接权或每一层之间的神经元都互相连接，并满足人工神经网络的三大要素（f（u）的函数类型、神经网络的结构、学习算法），则称为“霍普菲尔德模型”。

2）无监督学习人工神经网络：在有监督学习的人工神经网络中，神经网络的连接权的调整是为了使能量函数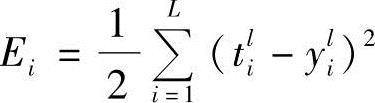最小化（t_i是“教师”，i=1，2，…，L）。而在无监督学习的人工神经网络中，在训练集中没有“教师”t_i，连接权的调整反映了训练集本身的性质。

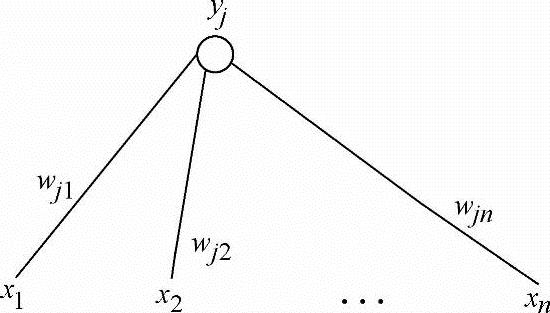
图7-17 监督学习人工神经网络模型

赫布学习规则是无监督学习中的常用规则。赫布学习规则为

Δw_ji=ηx_iy_i

式中，x_i为一个神经元的输出；y_i为另一个神经元的输出；η为调整步长；Δw_ji为x_i、y_i神经元之间的连接权的调整值。在无“教师”t和d时，神经元之间的连接权也可自动学习。它是一个局部的权的调整。这样的学习，最终导致了神经网络内部的自组织，从无序到有序，用赫布学习规则来学习的权可以有联想、记忆的作用。在式中，y_i加入了一个“教师”，就变成了有监督学习，Δw_ji=ηx_i（y_i-t_i）。

（4）神经网络模型 神经网络模型是人工神经网络研究的一个重要方面，目前已经开发出了多种不同的模型。由于这些模型大都是针对各种具体应用开发的，因而差别较大，至今尚无一个通用的神经网络模型。

1）感知器：感知器的学习是神经网络最典型的学习。目前，在控制上应用的是多层前馈网络。下面介绍的是一种感知器模型，学习算法是BP算法，属于有教师学习算法。一个有教师的学习系统如图7-18所示。这种学习系统分成三个部分：输入部、训练部和输出部。

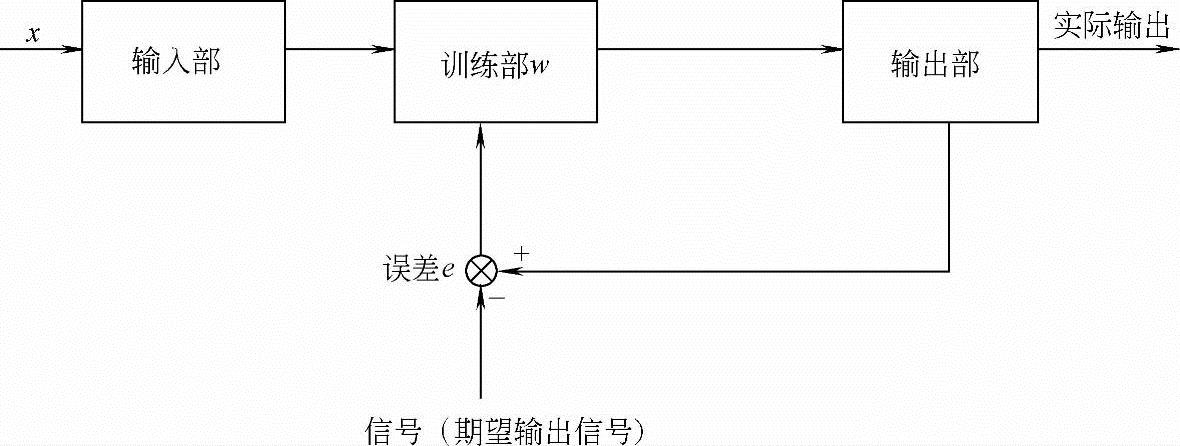
图7-18 神经网络学习系统框图

输入部接收外来的输入样本x，由训练部进行网络的权值w调整，然后由输出部输出结果。在这个过程中，期望的输出信号可以作为教师信号输入，由该教师信号与实际输出进行比较，产生的误差去控制修改权值w。

学习结构如图7-19所示。

在图7-19中，x₁，x₂，…，x_n是输入样本信号；w₁，w₂，…，w_n是权系数。输入样本信号x_i可以取离散值“0”或“1”。输入样本信号通过权值作用，在u处产生输出结果∑w_ix_i，即有

u=∑w_ix_i=w₁x₁+w₂x₂+…+w_nx_n （7-168）

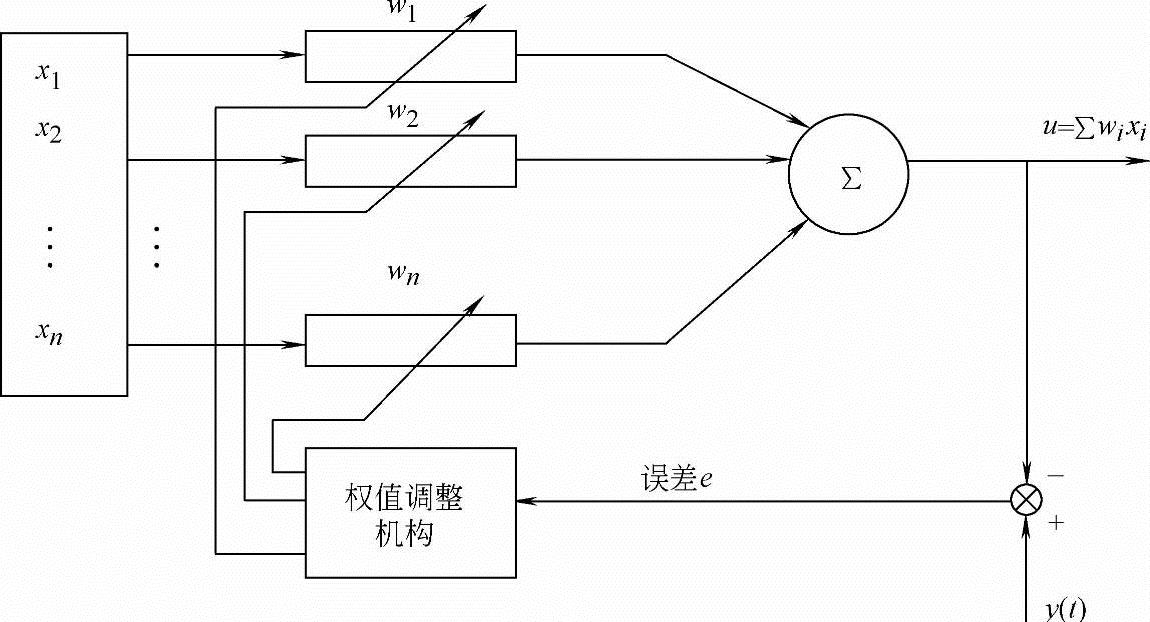
图7-19 神经网络学习结构框图

再把期望输出信号y（t）和u进行比较，从而产生误差信号e。即权值调整机构根据误差e去对学习系统的权系数进行修改，修改方向应使误差e变小，不断进行下去，直到误差e为零，这时实际输出值u和期望输出值y（t）完全一样，则学习过程结束。(www.xing528.com)

神经网络的学习一般需要多次重复训练，使误差值逐渐趋向零，最后到达零，这时才会使输出与期望一致。故而神经网络的学习是消耗一定时间的，有的学习过程要重复很多次，甚至达万次级。原因在于神经网络的权系数w有很多分量w₁，w₂，…，w_n，也就是说它是一个多参数修改系统。系统参数的调整就必定耗时耗量。目前，提高神经网络的学习速度、减少学习重复次数是十分重要的研究课题，也是实时控制中的关键问题。

感知器的学习目的是在于修改网络中的权值，使网络对于所输入的模式样本能正确分类。当学习结束时，也即神经网络能正确分类时，显然权系数就反映了同类输入模式样本的共同特征。换句话说，权系数就是存储了的输入模式。由于权系数是分散存在的，故神经网络自然而然就有分布存储的特点。

前面的感知器的传递函数是阶跃函数，所以它可以用作分类器，但其学习算法因其传递函数的简单而存在局限性。

感知器学习算法相当简单，并且当函数线性可分时保证收敛。但它也存在问题：即函数不是线性可分时，则求不出结果；另外，不能推广到一般前馈网络中。

为了克服存在的问题，所以人们提出另一种算法，即梯度算法[也称最小均方（LMS）法]。为了能实现梯度算法，故把神经元的激发函数改为可微分函数，例如Sigmoid函数，非对称Sigmoid函数为

f（x）=1/（1+e-x） （7-169）

对称Sigmoid函数为

f（x）=（1-e-x）/（1+e-x） （7-170）

对于给定的样本集x_i（i=1，2，…，n），梯度算法的目的是寻找权值w^*，使得f[w^*，x_i]与期望输出y_i尽可能接近。

设误差e采用下式表示：

式中，y_i=f[w^*，x_i]是对应第i个样本x_i的实时输出。y′_i是对应第i个样本x_i的期望输出。要使误差e最小，可先求取e的梯度，即

式中

令u_k=wx_k，则有

即有

最后有按负梯度方向修改权值w的修改规则为

也可写成

在式（7-176）和式（7-177）中，μ是权重变化率，它视情况不同而取值不同，一般取0～1之间的小数。

很明显，梯度法比原来感知器的学习算法进了一大步。其关键在于两点：

①神经元的传递函数采用连续的s型函数，而不是阶跃函数。

②对权系数的修改采用误差的梯度去控制，而不是采用误差去控制，故而有更好的动态特能，即加强了收敛进程。但是梯度法对于实际学习来说，仍然是感觉太慢，所以这种算法仍然是不理想的。

反向传播算法也称BP算法。由于这种算法在本质上是一种神经网络学习的数学模型，所以有时也称为BP模型。

BP算法是为了解决多层前向神经网络的权系数优化而提出来的，所以BP算法也通常暗示着神经网络的拓扑结构是一种无反馈的多层前向网络，故而有时也称无反馈多层前向网络为BP模型。

2）BP模型：BP模型是一种用于前向多层神经网络的反向传播学习算法，由鲁梅尔哈特（D.Ruvmelhar）和麦克莱伦德（McClelland）于1985年提出。BP算法用于多层网络，网络中不仅有输入层节点及输出层节点，而且还有一层至多层的隐层节点，如图7-20所示。

当有信息向网络输入时，信息首先由输入层传至隐层节点，经特性函数作用后，再传至下一隐层，直到最终传至输出层进行输出，其间每经过一层都要由相应的特性函数进行变换，节点的特性函数通常选用S型函数，例如：

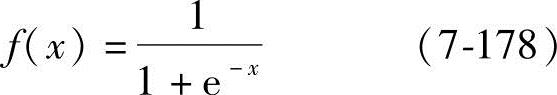
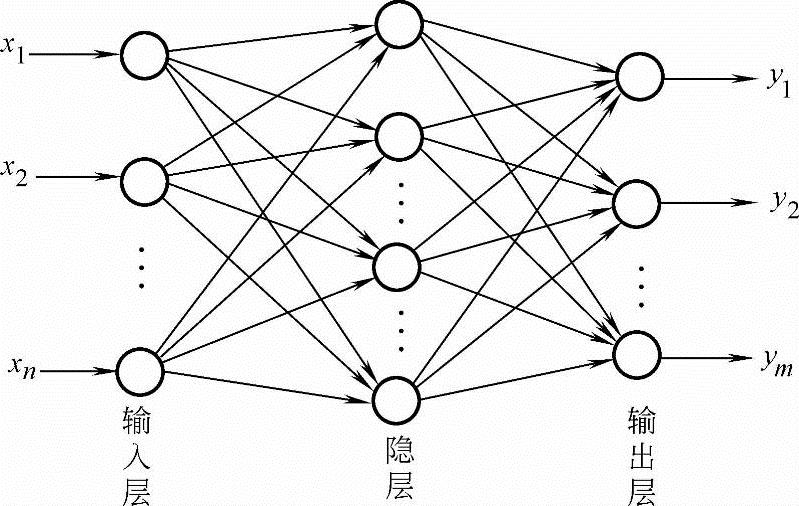
图7-20 BP网络

算法学习的目的是对网络的连接权值进行调整，使得对任一输入都能得到所期望的输出。学习的方法是用一组训练样例对网络进行训练，每一个样例都包括输入及期望的输出两部分。训练时，首先把样例的输入信息输入到网络中，由网络从第一个隐层开始，逐层地进行计算，并向下一层传递，直至传至输出层，其间每一层神经元只影响下一层神经元的状态。然后，以其输出与样例的期望输出进行比较，如果它们的误差不能满足要求，则沿着原来的连接通路逐层返回，并利用两者的误差按一定的原则对各层节点的连接权值进行调整，使误差逐步减小，直到满足要求时为止。

BP算法学习的具体步骤：

● 从训练样例集中取一样例，把输入信息输入到网络中。

● 由网络分别计算各层节点的输出。

● 计算网络的实际输出与期望输出的误差。

● 从输出层反向计算到第一个隐层，按一定原则向减小误差方向调整网络的各个连接权值。

● 对训练样例集中的每一个样例重复以上步骤，直到对整个训练样例集的误差达到要求时为止。

3）Hopfield模型：前面讨论的两种模型都是前向神经网络，从输出层至输入层无反馈，这就不会使网络的输出陷入从一个状态到另一个状态的无限转换中，因而人们对它的研究是着重学习方法的研究，而较少关心网络的稳定性。

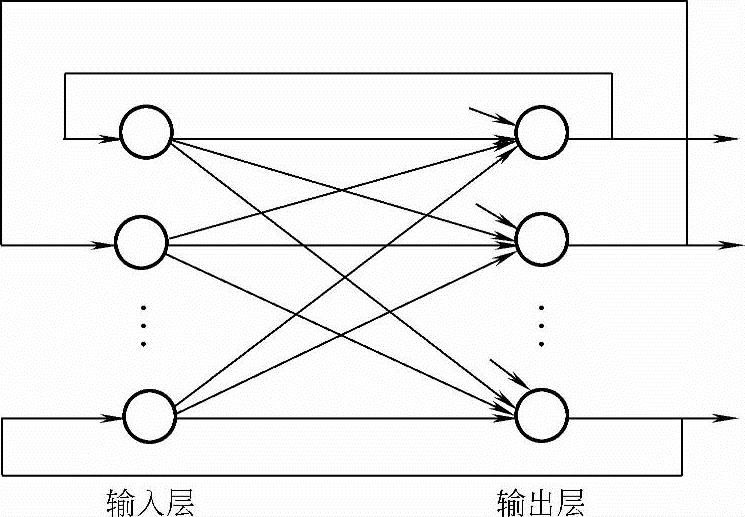
图7-21 单层反馈神经网络

Hopfield模型是霍普菲尔特（Hopfield）分别于1982年及1984年提出的两个神经网络模型：一个是离散的；另一个是连续的。但它们都属于反馈网络，即它们从输入层至输出层都有反馈存在。图7-21所示为一个单层反馈神经网络。

在反馈网络中，由于网络的输出要反复地作为输入送入网络中，这就使得网络的状态在不断地改变，因而就提出了网络的稳定性问题。所谓一个网络是稳定的，是指从某一时刻开始，网络的状态不再改变。设用X（t）表示网络在时刻t的状态，如果从t=0的任一初态X（0）开始，存在一个有限的时刻t，使得从此时刻开始神经网络的状态不再发生改变，即

X（t+Δt）=X（t） Δt＞0 （7-179）

就称该网络是稳定的。

下面给出Hopfiled模型的算法：

● 设置互连权值

式中，x^s_i为s类样例的第i个分量，它可以为+1或-1（0），样例类别数为m，节点数为n。

● 未知类别样本初始化

y_i（0）=x_i 1≤i≤n （7-181）

式中，y_i（t）为节点i在t时刻的输出，当t=0时，y_i（0）就是节点i的初始值；x_i为输入样本的第i个分量。

● 迭代直到收敛。