隐马尔可夫模型在实际应用中要解决的三个基本问题:
问题1:给定观察序列O=O1,O2,…,OT和λ=(π,A,B),怎样有效地计算P(O|λ),即给定模型的观察序列的概率?
问题2:给定观察序列O=O1,O2,…,OT和模型λ,怎样选择另一个状态序列Q*=q1*,q2*,…,qT*,使它在某种意义下是最佳的(即最好地解释观察情况)?
问题3:怎样调整模型参数λ=(π,A,B),使P(O|λ)最大?
这三大基本问题的解决过程与方法,即是HMM实际应用的过程与方法,可以从下面的角度理解:估计问题,即模型评价——前向算法和后向算法;解码问题,即最优状态序列求解——Viterbi算法;学习问题,即模型参数估计——Baum-Welch算法。
1.HMM模型评价(Model Evaluation)
HMM是将实时信号源作为马尔可夫信号源或马尔可夫链的概率函数的一种统计模型,假定信号是模型输出的观察值序列,当使用HMM作为分类目的时,通常假定观察值序列是由唯一信号源产生的,而分类的目的就是决策这个观察值序列是由哪一个信号源产生的,于是将每一种信号源用相应的HMM来建模,当输入一个未知模式的观察值序列到某一HMM信号模型时,应该对其生成概率模型进行评价。
最后将产生观察值序列的最大生成概率的第I个HMM模型作为该信号的HMM源,也就是将这一个未知模式分到I类中去:
x∈i,如果maxP(Ox|λi),那么x∈i
前向-后向算法是用来计算给定一个观察值序列O=O1,O2,…,OT,以及一个模型λ=(π,A,B)时,由模型λ产生出O的概率P(O|λ)。
根据图7-13所示的HMM的组成,P(O|λ)最直接的求取方法如下:
对一个固定的状态序列S=q1,q2,…,qT,有
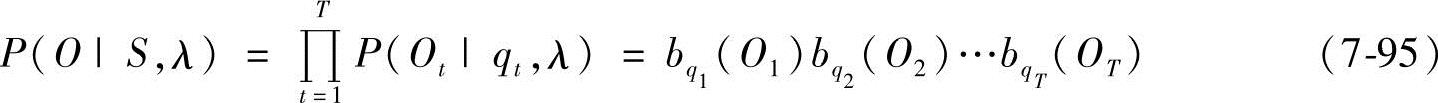
式中
bqt(Ot)=bjk|qt=θj,Ot=Vk,1≤t≤T (7-96)
而对给定λ,产生S的概率为

因此,所求概率为
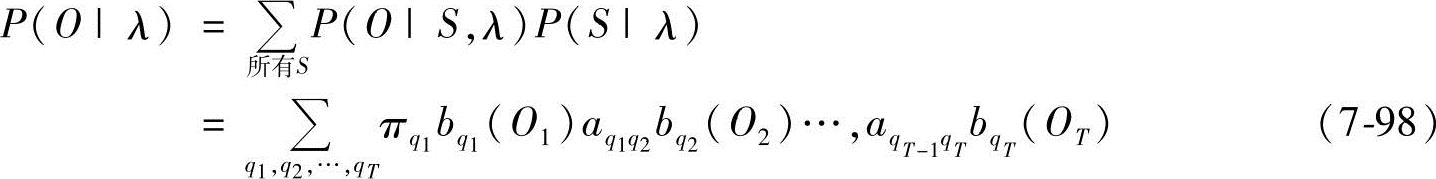
显而易见,上式的计算量是十分惊人的,大约为2TNT数量级,当N=5,T=100时,计算量达1072,这是完全不能接受的。在此情况下,要求出P(O|λ),还必须寻求更有效的算法,这就是Baum等人提出的前向-后向算法。
(1)前向算法 定义前向变量为
α(i)=P(O1,O2,…,Ot,qt=θi|λ) 1≤t≤T (7-99)
那么,有
1)初始化:
α1(i)=πibi(O1) 1≤i≤N (7-100)
2)递归:
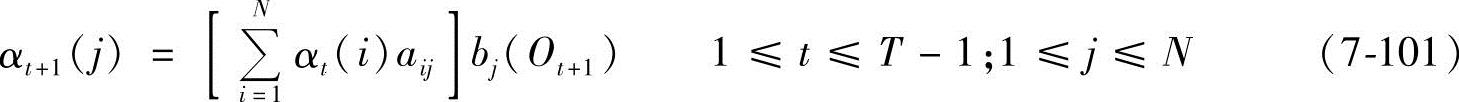
式中

3)终结:

这种算法计算量大为减少,变为N(N+1)(T-1)+N次乘法和N(N-1)(T-1)次加法。同样N=5、T=100时,只需大约3000次计算(乘法)。这种算法是一种典型的栅格结构,如图7-14所示。
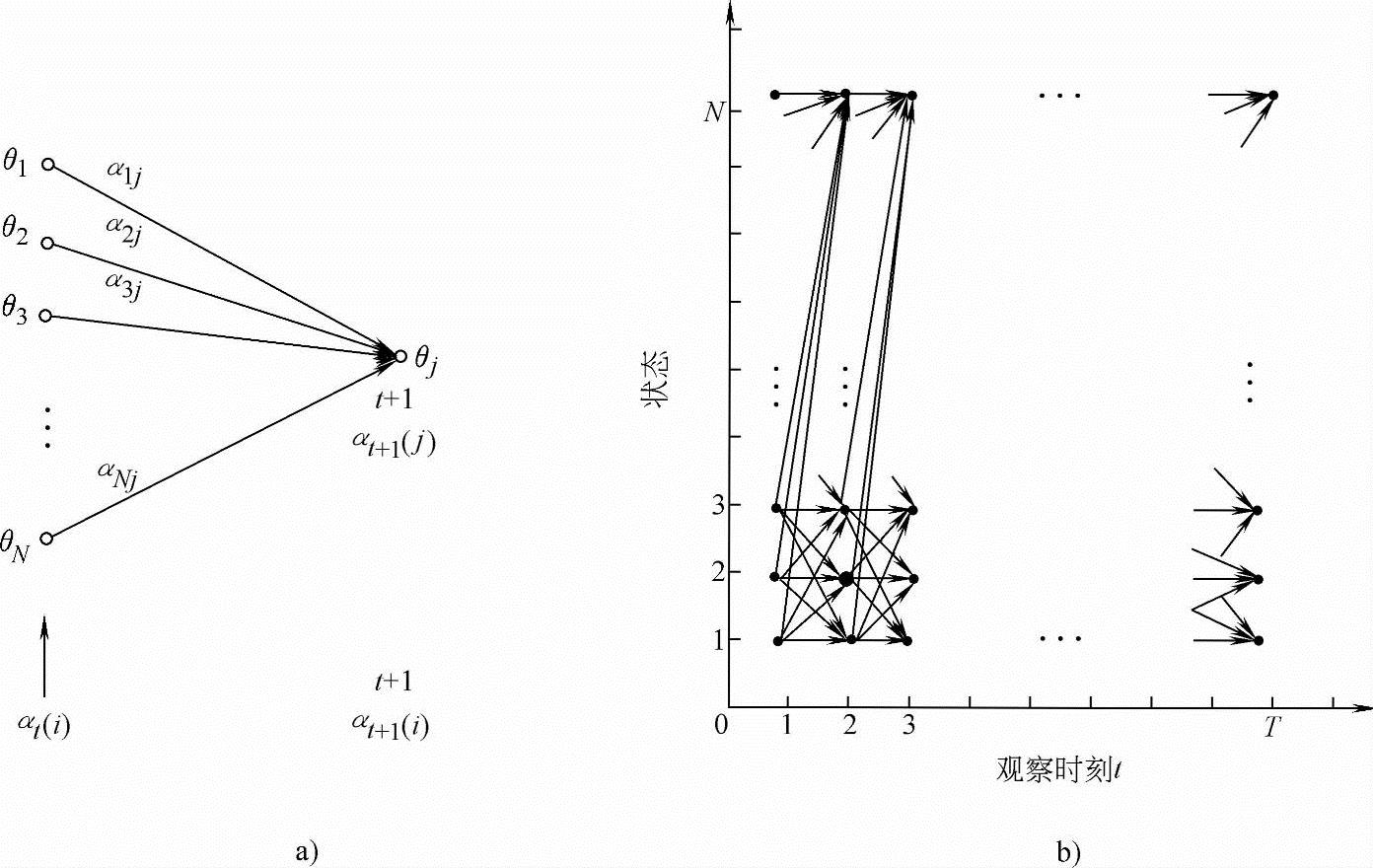
图7-14 前向算法示意图
a)t时刻递归关系 b)栅格结构
(2)后向算法 与前向算法类似,定义后向变量为
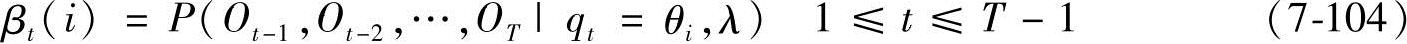
那么,有
1)初始化:
βT(i)=1 1≤i≤N (7-105)
2)递归:
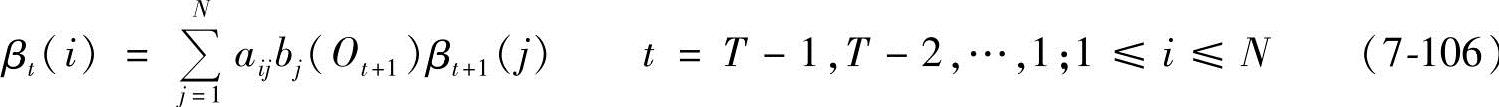
3)终结:

后向算法的计算量大约在N2T数量级,也是一种栅格结构。
2.HMM最优状态序列求解
给定观察序列O=O1,O2,…,OT和模型λ,怎样选择另一个状态序列Q*=q1*,q2*,…,qT*,使它在某种意义下是最佳的(即最好地解释观察情况)?
Viterbi算法解决了给定一个观察值序列O=O1,O2,…,OT和一个模型λ=(π,A,B),在最佳的意义上确定一个状态序列Q*=q1*,q2*,…,qT*的问题。
“最佳”的意义有很多种,由不同的定义可得到不同的结论。这里讨论的最佳意义上的状态序列Q*,是指使P(Q,O|λ)最大时确定的状态序列Q*。Viterbi算法可以叙述如下:
定义δt(i)为时刻t时沿一条路径q1,q2,…,qt,且qt=θi,产生出O1,O2…,Ot的最大概率,即有
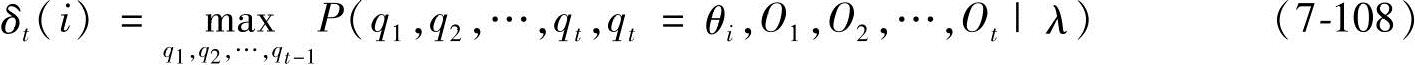
那么,求取最佳状态序列Q*的过程为:
1)初始化:
δ1(i)=πibi(O1) 1≤i≤N (7-109)
φ1(i)=0 1≤i≤N (7-110)
2)递归:
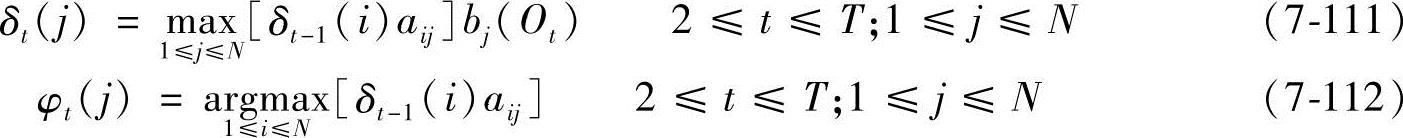
3)终结:
 (https://www.xing528.com)
(https://www.xing528.com)
求取状态序列:得
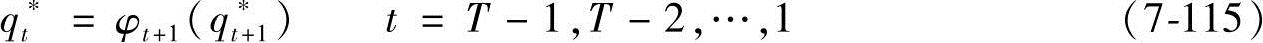
应当指出,Viterbi算法的一个副产品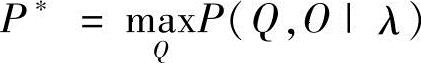 和前向-后向算法计算出的
和前向-后向算法计算出的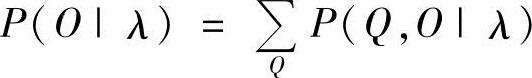 之间的关系为:对语音信号应用而言,P(Q,O|λ)动态范围很大,或者说不同的Q使P(Q,O|λ)的值差别很大,而
之间的关系为:对语音信号应用而言,P(Q,O|λ)动态范围很大,或者说不同的Q使P(Q,O|λ)的值差别很大,而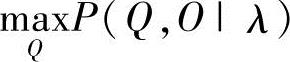 事实上是
事实上是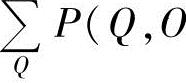
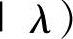 中举足轻重的唯一成分,因此常常等价地使用
中举足轻重的唯一成分,因此常常等价地使用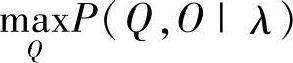 和
和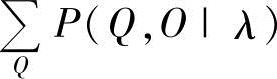 ,那么,Viterbi算法也能用来计算P(O|λ)。
,那么,Viterbi算法也能用来计算P(O|λ)。
此外,上述的Viterbi算法也是一种栅格结构,而且类似于前向算法。同样,由后向算法的思想出发,亦可推导出Viterbi算法的另一种实现方式。
3.HMM模型参数估计
HMM模型参数估计(Model Parameteres Estimating)是HMM模型的一个关键问题,一个模型设计得是否合理,或者说是否可以用该HMM模型来描述此类信号,最终体现在是不是能够通过大量的观察值样本训练出收敛的HMM参数,并使模型具有推广的能力。HMM模型参数估计准则是给定一个观察序列O=O1,O2,…,ON,通过某种算法对HMM模型参数进行调整,最终确定一个λ=(π,A,B),使得P(O|λ)最大。
(1)Baum-Welch算法 这个算法实际上是解决HMM训练,即HMM参数估计问题,或者说给定一个观察值序列O=O1,O2,…,OT,该算法能确定一个λ=(π,A,B),使P(O|λ)最大。
显然,由式(7-99)和式(7-104)定义的前向和后向变量有
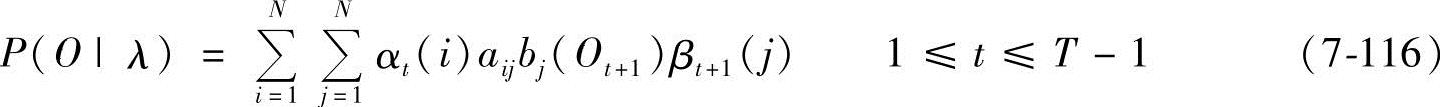
这里,求取λ,使P(O|λ)最大,是一个泛函极值问题。但是由于给定的训练序列有限,因而不存在一个最佳的方法来估计λ。在这种情况下,Baum-Welch算法利用递归的思想,使P(O|λ)局部极大,最后得到模型参数λ=(π,A,B)。此外,用梯度方法也可以达到类似的目的。
定义ξt(i,j)为给定训练序列O和模型λ时,时刻t时马尔可夫链处于θi状态和时刻t+1处于θj状态的概率,即
ξt(i,j)=P(O,qt=θi,qt+1=θj|λ) (7-117)
可以推导出:
ξt(i,j)=[αt(i)aijbj(Ot+1)βt+1(j)]/P(O|λ) (7-118)
那么,时刻t时马尔可夫链处于θi状态的概率为
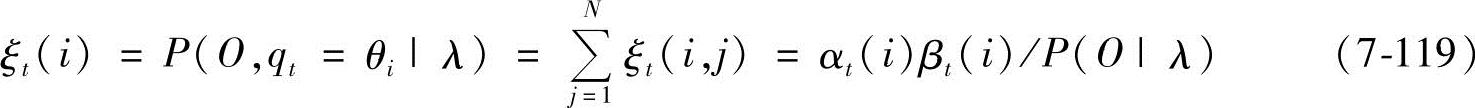
因此,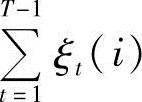 表示从θi状态转移出去的次数的期望值,而
表示从θi状态转移出去的次数的期望值,而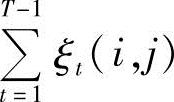 表示从θi状态转移到θj状态的次数的期望值。由此,导出了Baum-Welch算法中著名的重估(Reestimation)公式:
表示从θi状态转移到θj状态的次数的期望值。由此,导出了Baum-Welch算法中著名的重估(Reestimation)公式:
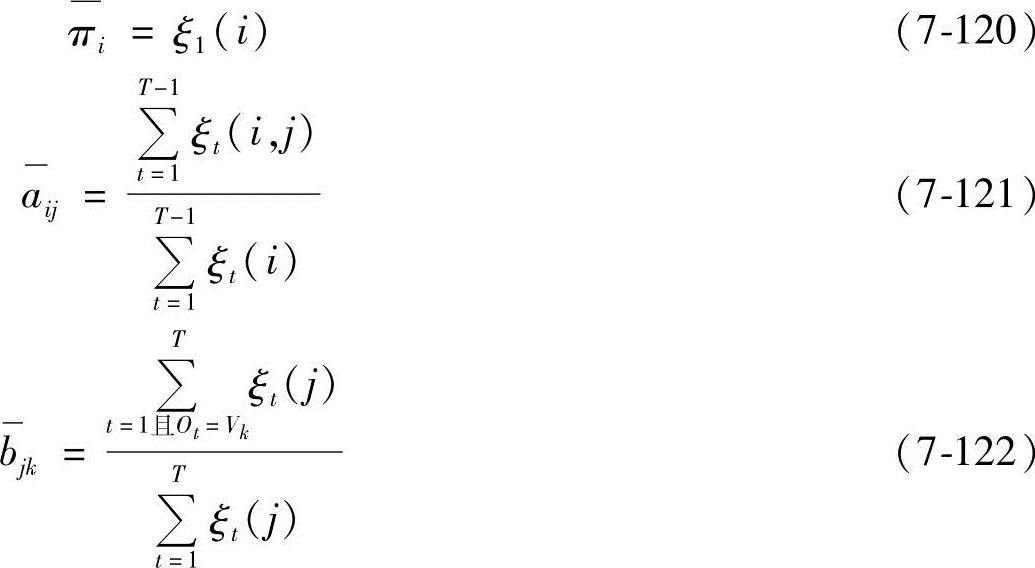
那么,HMM参数λ=(π,A,B)的求取过程为:根据观察值序列O和选取的初始模型λ=(π,A,B),由重估式(7-120)、式(7-121)和式(7-122),求得一组新参数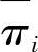 、
、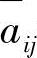 和
和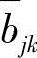 ,亦即得到了一个新的模型
,亦即得到了一个新的模型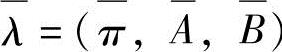 ,可以证明
,可以证明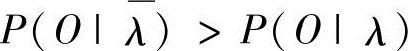 ,即由重估公式得到的
,即由重估公式得到的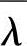 比λ在表示观察值序列O方面要好。那么,重复这个过程,逐步改进模型参数,直到
比λ在表示观察值序列O方面要好。那么,重复这个过程,逐步改进模型参数,直到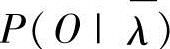 收敛,即不再明显增大,此时的λ即为所求的模型。
收敛,即不再明显增大,此时的λ即为所求的模型。
应当指出,HMM训练或称参数估计问题,是HMM在模式识别中应用的关键问题,与前面讨论的两个问题相比,这也是最困难的一个问题,Baum-Welch算法只是得到广泛应用的解决这一问题的经典方法,但并不是唯一的,也远不是最完善的方法。
(2)HMM的最佳化准则 分类器设计的准则决定着分类器的分类性能。HMM的基本原则是,如果正确地选择参数,信号(或观察序列)就可被很好地模拟。传统的HMM参数估计方法采用Baum-Welch算法或EM(期望最大化)算法,它实际上是一种最大似然(ML)法。最大似然法假定一系列彼此独立的随机采样x={x1,x2,…,xn},x服从概率分布Pn(x|Φ),其中参数Φ属于某参数空间Ω。给定一观察向量x={x1,x2,…,xn},Φ对该向量的似然度定义为联合概率分布Pn(x|Φ),也称为似然函数。最大似然估计(MLE)认为,似然函数的形式是固定的,而似然函数中各参数的值未知,参数估计的目的即是寻找一组参数值,以使似然函数对各个观察向量的似然度达到最大化。如假设Pn(x|Φ)是一高斯分布函数N=(m,Σ),Φ即包括均值m及方差Σ,值得强调的是,这里Φ不是一个随机向量,而是某个固定而未知的参数向量。由于x1,x2,…,xn是彼此间独立的随机变量,似然函数可以重写为

Φ的最大似然估计可以被定义为

这种估计方法经常被称为最大似然估计(MLE)。由于对数函数是单调递增函数,因此式(7-120)同下式等价:
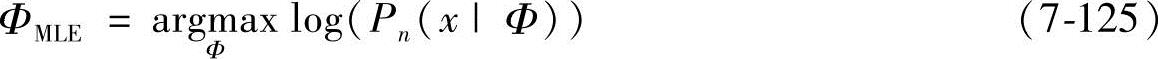
设log(Pn(x|Φ))为一连续可导函数,则ΦMLE可通过解下列偏导方程组获得

最大似然估计可被证明是一致的。“一致性”意味着,当训练数据足够多时,参数估计可收敛到真正的概率分布形式。
Nakata等人的研究结果表明,如果模型能够表示数据的实际分布(即如果模型中对数据分布形式的假设是正确的),且有足够的训练数据,那么极大似然估计就是实际参数的最佳估计。例如,如果数据分布是高斯的,则高斯概率函数的均值和方差的极大似然估计就是实际均值和方差的最佳估计。采用EM算法,极大似然估计可以有效地用于HMM。
然而,以最大似然度为优化目标的分类器无法得到理想的性能。这是因为假设的参数分布形式与实际分布形式是有差异的。依据假设的分布形式而进行的参数优化与分类器的最佳优化(即对误识率的优化)是不一样的。所以训练无法得到最佳性能。为解决这些问题,出现了许多不同的分类器参数估计准则,如最大互信息(Maximum Mutual Information)法、最小鉴别信息(Minimum Discriminative Information)法、校正训练(Corrective Training)法、最大模型距离(Maximum Model Distance)法等。尽管与传统的ML法准则相比,这些新方法有显著的优点,但它们优化的目标也不是直接和分类误差联系在一起的,因此仍有改进的余地。最小分类错误(MCE)法正是实现了这种改进的新算法,它通过直接最小化分类误差来实现分类器的设计,也就是说,MCE训练的目标不是使模型更符合训练数据的分布,而是使模型的分类结果(识别)最好。
(3)最小分类/错误准则 20世纪90年代以来,Juang等学者提出了最小分类错误(MCE)准则。MCE训练算法是一种判别训练算法。它的提出是为了修正传统的判别训练算法的缺点。基于这种准则的训练算法的目的是为分类器找出合适的参数集,以使分类错误最小[35]。它将训练的目标函数与误识率直接联系起来,当目标函数下降时,系统的误识率也随之一致性下降。这种方法从改进训练的效果入手,能够有效地区分易混淆的模型,从而减少分类错误率。这种训练算法在很多模式识别的领域中得到了成功的应用,例如语音识别、手写字符识别等。
优化准则:对于一个输入向量,分类器通过以下决策规则来进行决策:
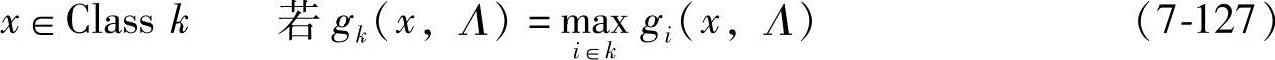
式中,gi(x,Λ)是x属于第I类的程度的判别函数;Λ是参数集;k是类的数量。
gk(x,Λ)=P(x|λ(i))=P(x|π(i),A(i),B(i)) (7-128)
这个准则可以被重写为
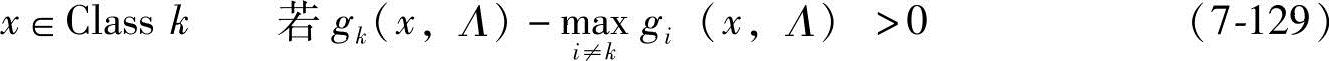
因此,函数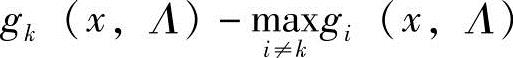 的值越高,特征向量x归为第k类的可靠性越大,这意味着能使用这个函数的负值作为x归类为第k类的误识率。
的值越高,特征向量x归为第k类的可靠性越大,这意味着能使用这个函数的负值作为x归类为第k类的误识率。
但有限数据训练集的分类函数(分类规则)对于分类器参数集A来说是个阶跃函数,因此它不利于用数值分析方法来优化。因此,需要定义一个误分类测度函数。
在参考文献[37]中,一个改进的误分类测度函数可以用下式表示:
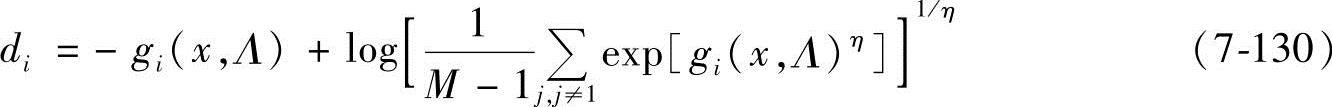
式中,η是误识别类识别函数的加权系数,是一个正的常数。当η趋近于∞,函数可以简化为
dk(x,Λ)=-gk(x,Λ)+gj(x,Λ) (7-131)
从式(7-131)中可以看出,若dk(x,Λ)>0,则意味着误识;若dk(x,Λ)<0,则表明正确的分类。
理想的损失函数能直接反映分类误差,即

由于其导数或者为零,或者没有定义,所以该损失函数不能用于基于梯度的最佳化方法。在MCE算法中,理想损失函数可以通过一个更适合梯度最佳化的连续的损失函数来近似。首先,一个与类相关的损失lk(x,Λ)可以定义为误分类测度函数:
lk(x,Λ)=l(dk(x,Λ)) (7-133)
l(Mk(x;Λ))的选择方式有很多种,如:
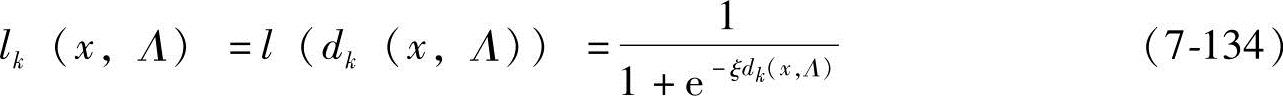
式中,ξ为正实数。可以看出,这种损失函数近似一个理想的二值损失函数,并且是连续的。对于一个训练集x,经验损失函数被定义为
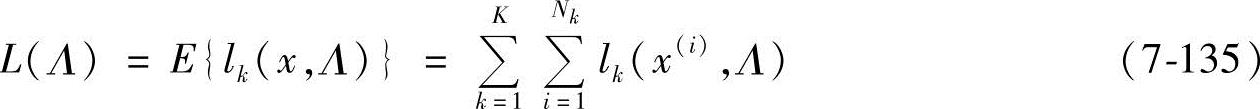
式中,Nk为类k的训练样本数。从上式中可以看出,最小化经验损失函数可以得到最小化的分类错误。分类参数集Λ可以通过最速梯度下降算法中最小化损失函数来获得。
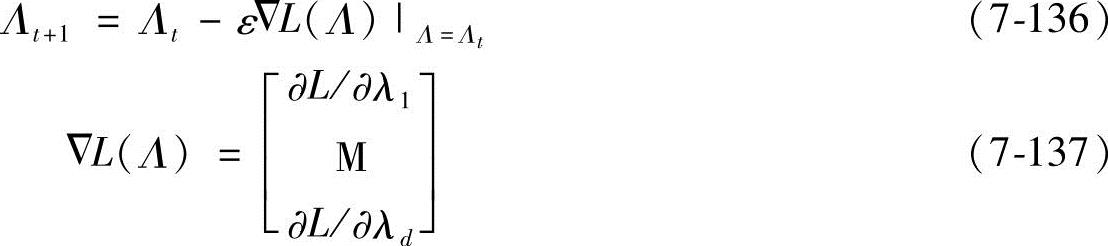
式中,Λt表示t时刻的Λ的状态,λ1,…λd∈Λ;ε为步长,ε>0。对于s=1,2,…,d,梯度ΔL(Λ)可以根据下式进行计算:
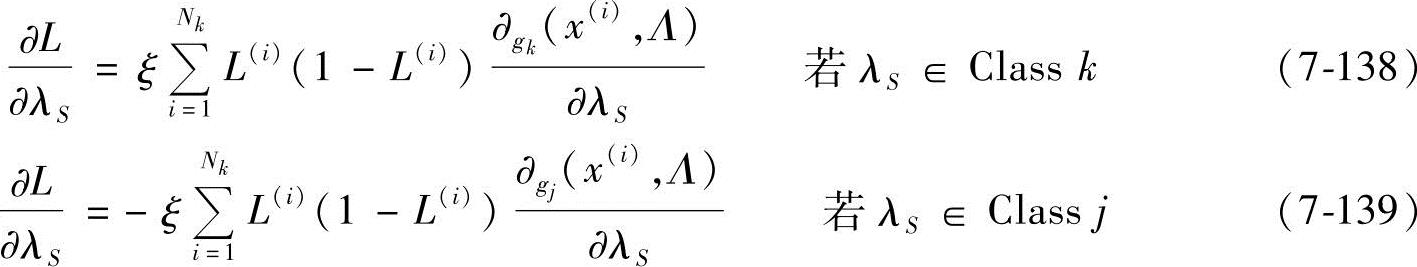
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




