1.马尔可夫过程
当过程在t=t0时所处的状态为已知的情况下,过程在时刻t(t>t0)所处的状态与过程在t=t0时刻之前的状态无关。这种已知“现在”的条件下,“将来”与“过去”无关的性质,就是直观意义下的马尔可夫性或称为无后效性。具有无后效性的过程称为马尔可夫过程。
【定义7-1】 给定随机过程{X(t),t∈T},如果对于参数中任意n个时刻ti,i=1,2,…,n;t1<t2<…<tn有
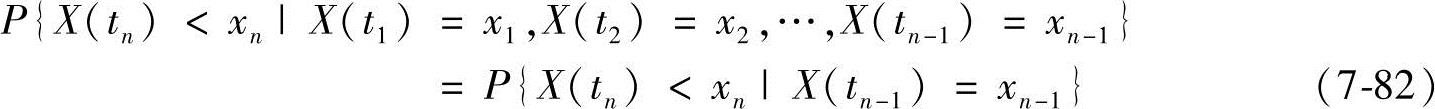
则称随机过程{X(t),t∈T}为马尔可夫过程,简称马氏过程。
随机过程具有马尔可夫性质是说,当给定X(t1),X(t2),…,X(tn-1)时,X(tn)的条件分布只依赖于X(tn-1)的已知值,而与在tn-1以前的X(t)的取值无关。
【定义7-2】 给定马尔可夫过程{X(t),t∈T},条件概率为
p(s,t,x,y)=P{X(t)<y|X(s)=x} (7-83)
称为马尔可夫过程的转移概率函数。
马尔可夫过程{X(t),t∈T}中X(t)的取值x称为状态,X(t)=x表示过程在时刻t,处于状态x,过程所有取值的全体E={x∶X(t)=x,t∈T}称为状态空间。
马尔可夫过程构成如下:
● 状态:以天气为例,有晴、阴、雨三种状态;
●πvector:时间为t0时,规定的系统状态初始概率;
● 状态转移矩阵:状态间转移的概率。
2.马尔可夫链
马尔可夫链是马尔可夫随机过程的特殊情况,即马尔可夫链是状态和时间参数都离散的马尔可夫过程。从数学上,可以给出如下定义:
随机序列Xn,在任一时刻n,它可以处在状态θ1,…,θN,且它在m+k时刻所处的状态为qm+k的概率,只与它在m时刻的状态qm有关,而与m时刻以前它所处状态无关,即有
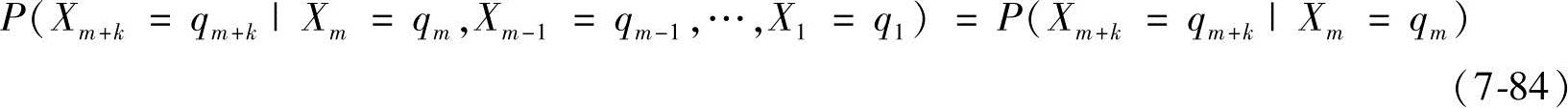
式中,q1,q2,…,qm,qm+k∈(θ1,θ2,…,θN),则称Xm为马尔可夫链,并且称

为k步转移概率,当Pij(m,m+k)与m无关时,称这个马尔可夫链为齐次马尔可夫链,此时
Pij(m,m+k)=Pij(k) (7-86)
以后若无特别申明,马尔可夫链就是指齐次马尔可夫链。当k=1时,Pij(1)称为一步转移概率,简称为转移概率,记为aij,所有转移概率aij(1≤i,j≤N)可以构成一个转移概率矩阵,即(https://www.xing528.com)

且有0≤aij≤1,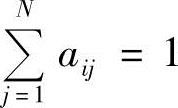 。
。
由于k步转移概率Pij(k)可由转移概率aij得到,因此,描述马尔可夫链的最重要参数就是转移概率矩阵A。但矩阵A还决定不了初始分布,即由A求不出q1=θi的概率,这样完全描述马尔可夫链,除矩阵A之外,还必须引进初始概率向量π=(π1,…,πN),其中
πi=P(q1=θi) 1≤i≤N (7-88)
显然,有0≤πi≤1,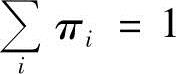 。
。
实际中,马尔可夫链的每一个状态可以对应于一个可观测到的物理事件。比如天气预测中的雨、晴、雪等,那么这时它可称之为天气预报的马尔可夫链模型。根据这个模型,可以算出各种天气(状态)在某一时刻出现的概率。例如:某处的晴天、下雨和下雪的天气情况分布如图7-10所示,要预测出连续六天是晴天、下雨、下雨、下雨、下雪和下雪的天气出现的概率。
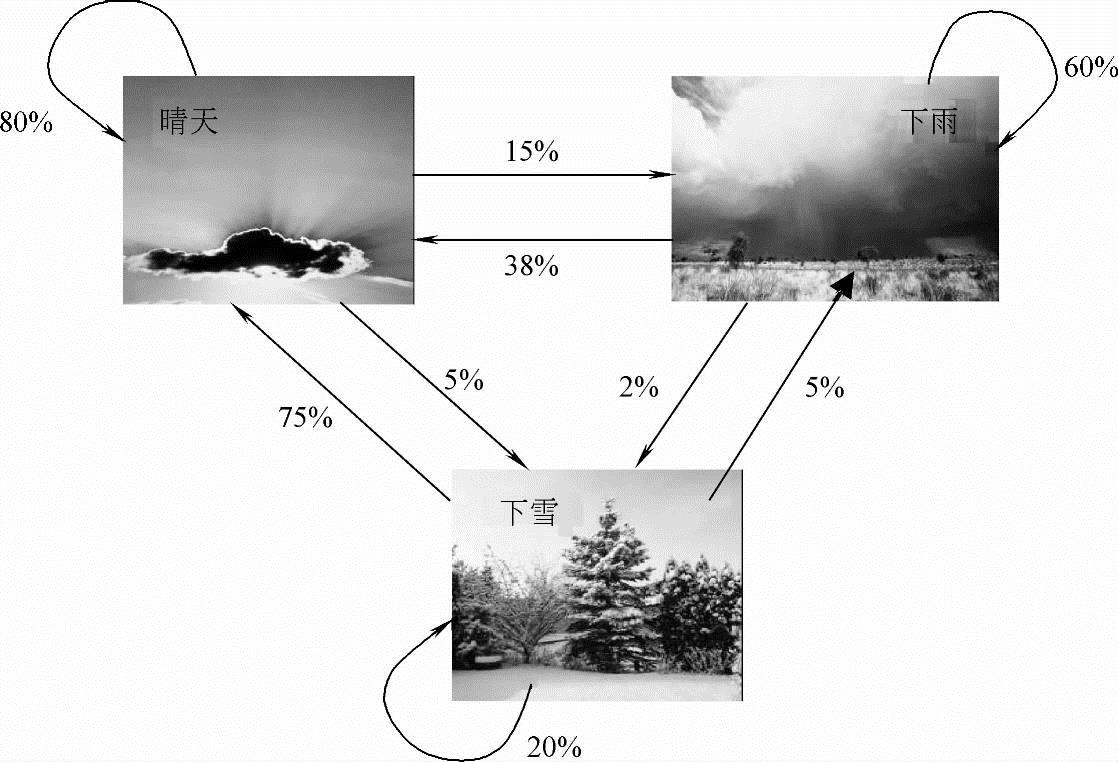
图7-10 天气分布图示
解:首先对于这个具体的问题已知马尔可夫链中主要的元素状态、转移概率和初始状态分别是
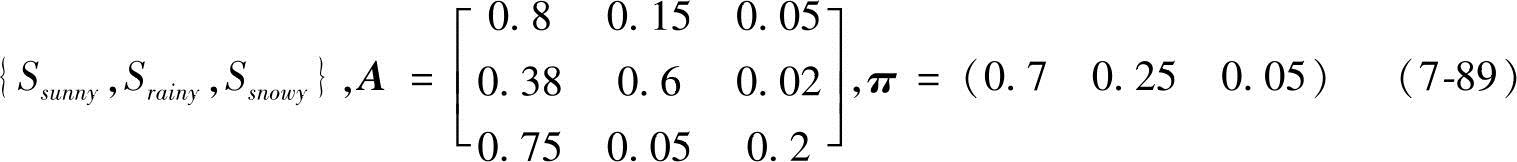
然后利用乘法定理计算出现连续六天是晴天、下雨、下雨、下雨、下雪和下雪的天气出现的概率,也就是图7-11所示的天气出现的概率。

图7-11 连续六天的天气图示
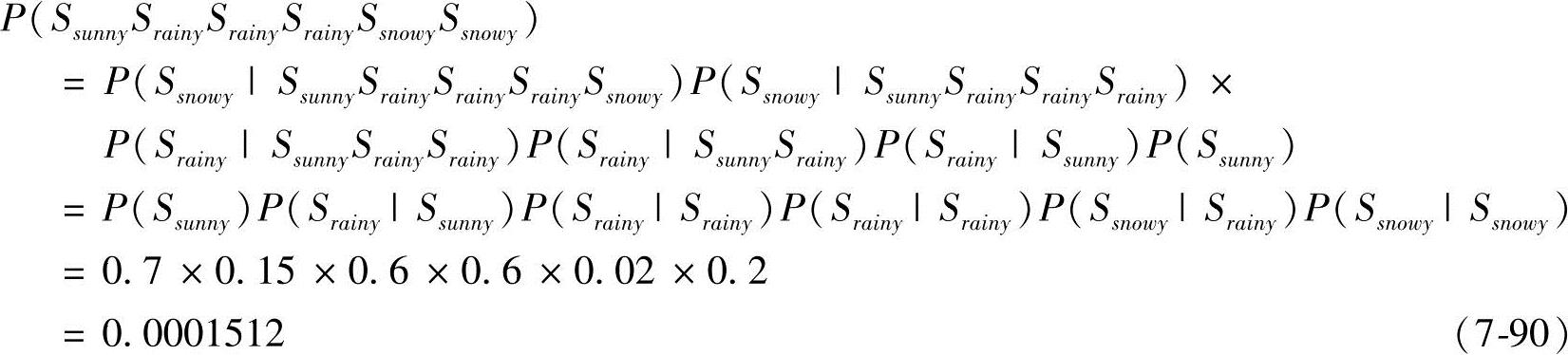
由此例可知:晴天—下雨—下雨—下雨—下雪—下雪可以看作是时间上离散的马尔可夫过程。
小结:马尔可夫模型的几个要素:
1)有N个状态,S1,S2…SN;
2)存在一个离散的时间序列t=0,t=1…
3)在每个时刻t,系统只能处于唯一一个状态qt;
4)下一个时刻所处的状态是随机出现的;
5)当前状态qt只与前面相邻的一个状态qt-1有关,与其他状态无关,即
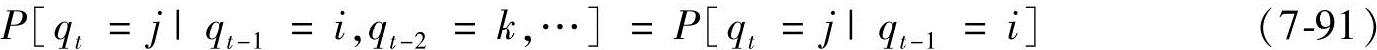
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




