贝叶斯网络分类器：高效而准确的分类方法

贝叶斯网络分类器是基于贝叶斯网络所建构的分类器。建立贝叶斯网络分类器可以被分为两个子阶段：第一阶段，网络拓扑学习，即有向非循环图的学习（简称结构学习），利用贝叶斯网络的学习算法，从实例数据建立由所有属性变量和类变量构成的贝叶斯网结构；第二阶段，网络中每个变量的局部条件概率分布的学习（简称参数学习），采用贝叶斯网络的推理算法计算给定属性变量的值，获得类变量的最大后验概率。

1.贝叶斯网络分类模型

贝叶斯分类模型是一种典型的基于统计方法的分类模型。贝叶斯定理是贝叶斯理论中最重要的一个公式，是贝叶斯学习方法的理论基础。它将事件的先验概率与后验概率巧妙地联系起来，利用先验信息和样本数据信息确定事件的后验概率。

令U={A₁，A₂，…，A_n，C}是离散随机变量的有限集，其中A₁，A₂，…，A_n是属性变量，类变量C的取值范围为{c₁，c₂，…，c_n}，a_i是属性A_i的取值。实例X_i={a₁，a₂，…，a_n}（字母X表示向量）属于类c_j的概率可由贝叶斯定理表示为

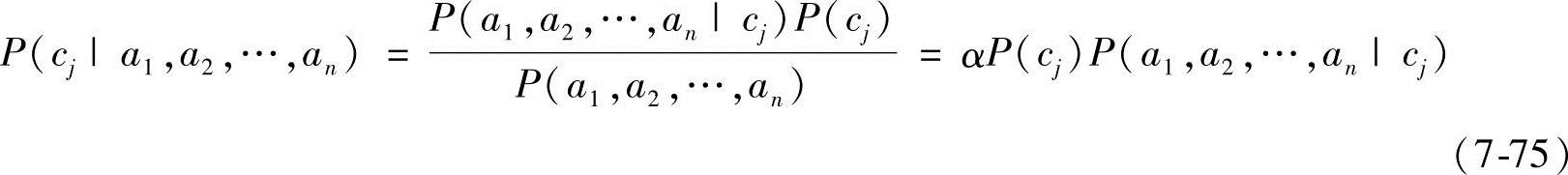
式中，α是正则化因子；P（c_j）是类c_j的先验概率；P（c_j|a₁，a₂，…，a_n）是类c_j的后验概率。先验概率独立于训练样本数据，而后验概率反映了样本数据对类c_j的影响。依据概率的链规则，式（7-75）可以表示为

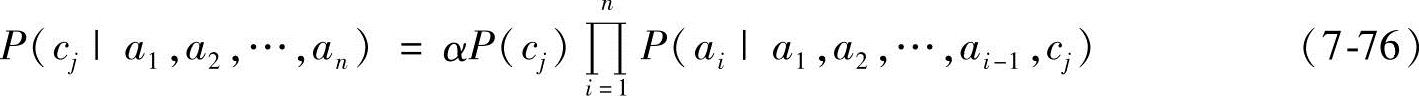
给定训练数据集D=（x₁，x₂，…，x_n），分类任务的目标是对数据集D进行分析，确定一个映射函数f：（A₁，A₂，…，A_n）→C，使得对任意的未知类别的实例X_i={a₁，a₂，…，a_n}可标以适当的类标签C^*。

根据贝叶斯最大后验准则，给定某一实例X_i={a₁，a₂，…，a_n}，贝叶斯分类器选择使后验概率P（c_j|a₁，a₂，…，a_n）最大的类标签C*作为该实例的类标签，即

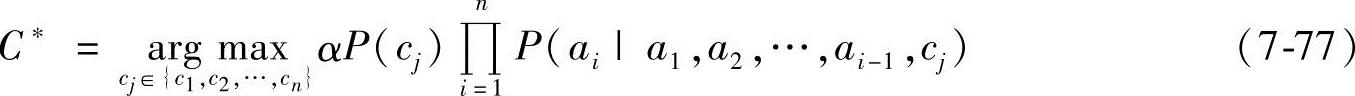
先验概率P（c_j）反映了已经拥有的关于类分布的背景知识，如果这个背景知识难以得到，那么可以简单地将每一候选假设赋予相同的先验概率，即认为所有的类服从均匀分布。确定先验概率的另一种方式是，采用训练数据中每个类的概率分布近似代替先验概率。

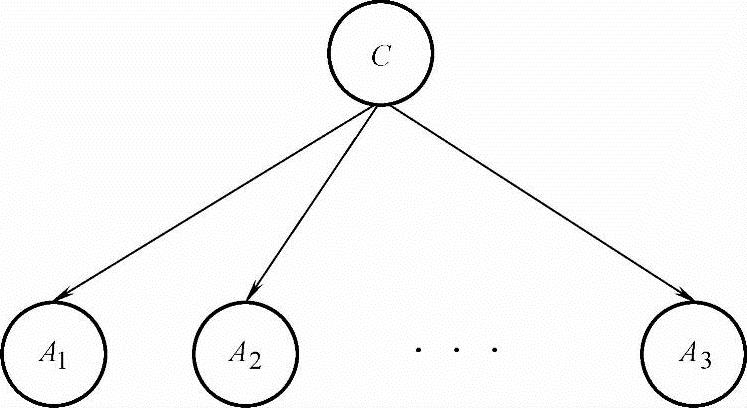
图7-5 朴素贝叶斯分类模型示意图

目前，不同贝叶斯分类模型的区别就在于，它们以不同的方式来求P（a_i|a₁，a₂，…，a_i-1，c_j）。贝叶斯分类模型的关键就是如何计算P（a_i|a₁，a₂，…，a_i-1，c_j）。下面介绍几种目前常用的贝叶斯网络分类器。

2.朴素贝叶斯分类器

朴素贝叶斯（Naive Bayes，NB）分类器可以看作是限制条件最严格的贝叶斯网络分类模型（见图7-5）。在朴素贝叶斯分类模型中，假定特征向量的各个属性变量间相对于类变量是相互独立的，也就是属性变量完全独立地作用于类变量。

在属性独立性假设条件下，条件概率P（a_i|a₁，a₂，…，a_i-1，c_j）简化为P（a_i|c_j），因此在朴素贝叶斯分类器中，实例X_i={a₁，a₂，…，a_n}属于类c_j的概率可表示为

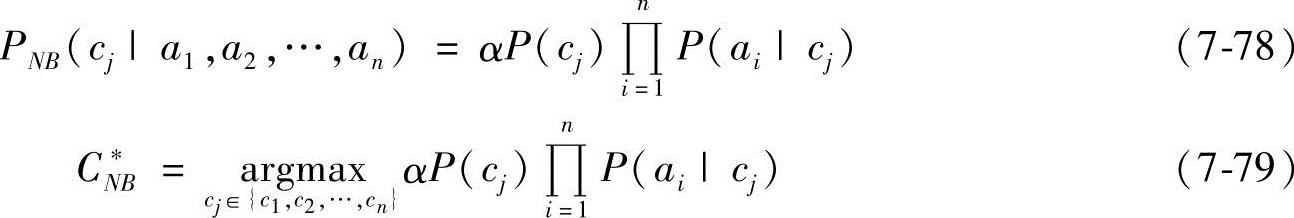
相对于其他分类方法，朴素贝叶斯分类器的最大特点是不需要假设空间的搜索，只需估计类先验概率和类条件概率。一种简单的估计方法是，从训练数据中，计算待分类实例中各个属性值在训练集中发生的频率数，估计出每个属性的概率估计值，因而朴素贝叶斯分类器的效率特别高。

朴素贝叶斯分类器是以一个很强的简单假设，即数据集的属性相对于类变量是相互独立的，为基础的。这个假设条件在现实世界的学习任务中是很少能够满足的。尽管Domingos和Pazzani己经发现，在某些情况下，属性独立性的违背对分类精度的影响会很小，但是在大多数实际情况下，该假设的违背会显著地降低预测精确度，于是人们开始研究如何减弱或放松属性独立性假设。

3.TAN分类器

树型扩展朴素贝叶斯分类器（Tree-Augmented Naive Bays classifier，TAN Classifier）是由Friedman等人提出的一种树型贝叶斯网络分类器，是朴素贝叶斯分类器的一种改进模型。TAN分类器的分类性能明显优于朴素贝叶斯分类器。其基本思路是放松朴素贝叶斯分类器中的独立性假设条件，在属性之间添加若干增强弧，并且保持增强弧连同属性节点构成树形结构。借鉴贝叶斯网络中表示依赖关系的方法，扩展朴素贝叶斯的结构，使其能容纳属性间存在的依赖关系，但对其表示依赖关系的能力加以限制。TAN将贝叶斯网络表示依赖关系的能力与朴素贝叶斯的简易性相结合，是学习的效率与准确地描述属性间相关性之间一个很好的折中。

在TAN树形结构中，

● 类节点是树的根节点，没有父节点，即Pa_C=φ；(www.xing528.com)

● 属性节点除了类结点以外最多只有1个父节点，即属性节点最多只有2个父节点。Pa_i≤2且C∈Pa_i（i=1，…，n）。

TAN分类器模型如图7-6所示。

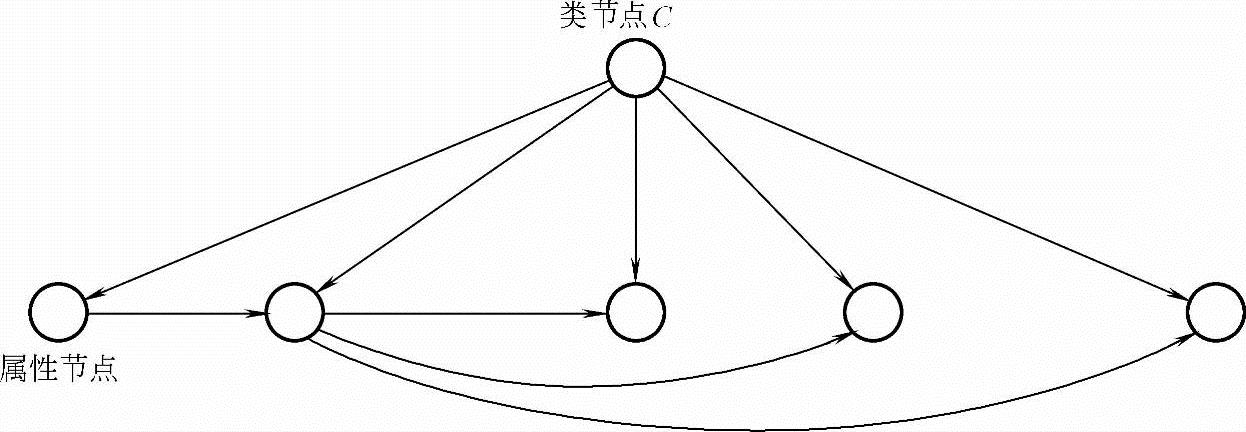
图7-6 TAN分类器模型示意图

因此，在朴素贝叶斯分类器中，实例X_i={a₁，a₂，…，a_n}属于类c_j的概率可表示为

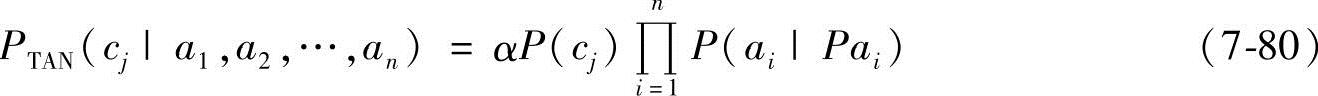
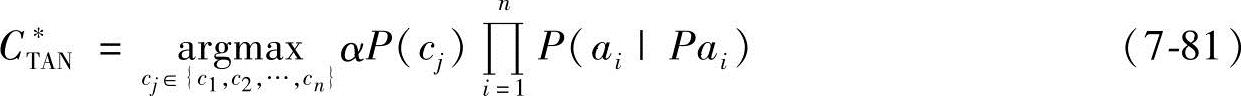
式中，P（a_i|Pa_i）或者是P（a_i|c_j），或者是P（a_i|a_p，c_i）a_p∈{a₁，a₂，…，a_i-1}。

与朴素贝叶斯分类器不同，TAN分类器需要有构造模型结构的学习算法。Friedman等人提出利用条件互信息来构造TAN分类器的算法。Keogh和Pazzani采用不同的思路构造TAN分类器，选择使分类精度改进最大的弧作为TAN的增强弧。这两种方法的不同之处在于，采用不同的评价准则来选择增强弧。

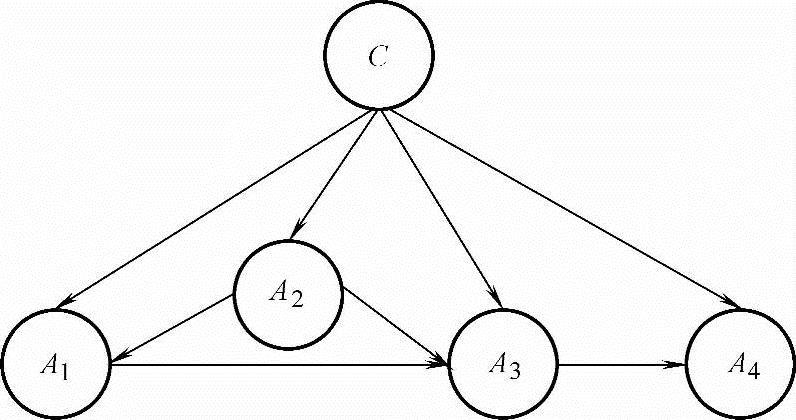
图7-7 BAN模型示意图

4.BAN分类器

扩展朴素贝叶斯的贝叶斯网络（Bayesian Network Augmented Naive Bayes，BAN）模型原则上对每个节点的父节点个数没有限定，只需按照事先选定的评价准则，在与属性节点A_i相关联的节点A₁，A₂，…，A_i-1，C中寻找A_i的父节点，每个节点A_i可以找出多个父节点，每个节点A_i的父节点可能不同。与一般贝叶斯网络的学习方法类似，BAN的学习有两种方式^[20，23]：启发式搜索方法和相关性分析方法。图7-7所示为BAN模型示意图。

BAN^[20，22]进一步扩展了TAN的结构，允许属性之间可以形成任意的有向图，使其表示依赖关系的能力增强，然而由于其结构的任意性，与一般贝叶斯网络一样，BAN结构的学习是不容易的（参考文献[24]已证明贝叶斯网络的学习是一个NP-Complete问题）。目前，并没有十分有效的学习这种结构的算法。

5.贝叶斯多网络分类器

贝叶斯多网络（Bayesian Multi-Net，BMN）模型结构是由多个子贝叶斯网络分类器组成的，每个子网的分类节点是类节点的一个取值，该节点的概率是类节点取值的先验概率，其余节点不变，BMN模型示意图如图7-8所示。这种结构是BAN的一种扩展。BAN强迫对每个类别下属性之间的关系都相同，而在BMN下，不同类别下的属性之间的关联可以不同。因而BMN的表达能力应该比BAN更强，比如在模式识别中，不同模式下特征之间的关系可能有很大差别。BMN并没有对各属性之间的关系作限制。BMN比BAN的结构可能更简洁，因为每个子网内的局部结构要比BAN简单，而在BAN中要表示出所有属性之间的关联可能需要更复杂的结构。

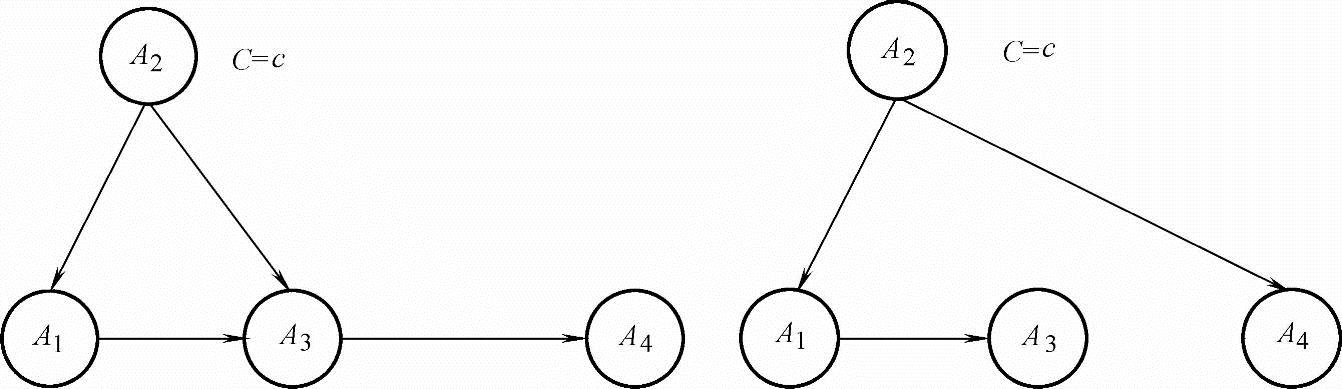
图7-8 BMN模型示意图

6.通用的贝叶斯网络分类器

前面几种结构都把类节点作为一种特殊的节点来对待，而通用贝叶斯网络（General Bayesian Network，GBN）把类节点与属性节点同样对待，如图7-9所示。这种结构学习需要获得一个完整的贝叶斯网络，而分类问题可以看作一种特殊的推理过程或决策问题。人们认为GBN中整个数据集只有一个单一的概率依赖关系，而BMN则允许每个类别下有一个概率依赖关系，因而当整个数据集具有单一分布时，GBN的性能会好些；当不同类别下的特征依赖关系差别较大时，BMN的性能要好些。

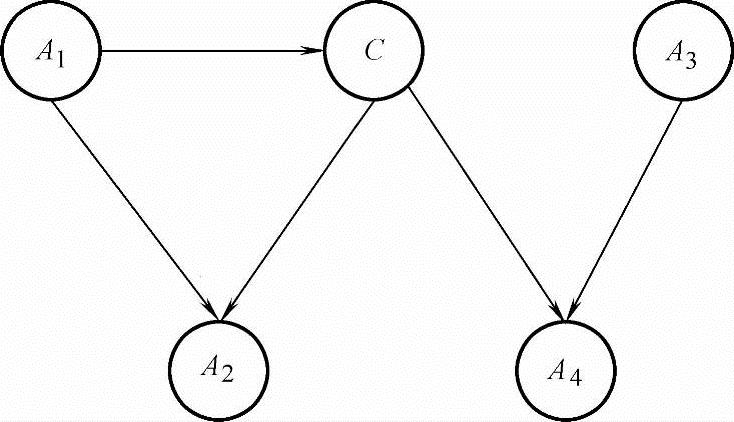
图7-9 GBN模型示意图