如何构建贝叶斯网络？

1.贝叶斯网络定义

贝叶斯网络又称为信念网络，是一种图形化的模型，能够图形化地表示一组变量间的联合概率分布函数。贝叶斯网络由两部分定义：一个结构模型和一组与之相关的条件概率分布函数。

结构模型是一个有向无环图，其中每个节点代表一个随机变量，是对于过程、事件、状态等实体的某特性的描述，变量可以是联系的，也可以是离散的。弧则表示变量间的概率依赖关系，如果一条弧由节点Y到Z，则Y是Z的双亲或直接前驱，而Z是Y的后继。图中两节点间若存在着一条弧，则表示与这两个节点相对应的随机变量是概率相依的，反之则说明这两个随机变量是相对独立的。

在贝叶斯网络结构中，任一节点x均和非x的父节点的子节点的各节点相对独立。网络中任一节点x均有一个相应的条件概率表（Conditional Probability Table，CPT），用以表示节点x在其父节点取各可能值时的条件概率。若节点x无父节点，则x的CPT为其先验概率分布。

图7-4所示为一个简单的贝叶斯网络模型。它有5个节点A_i（i=1，2，…，5）和5个弧段L_i（i=1，2，…，5）组成。图中没有输入的A₁节点称为根节点，一段弧的起始节点称为其末节点的母节点，而后者称为前者的子节点。

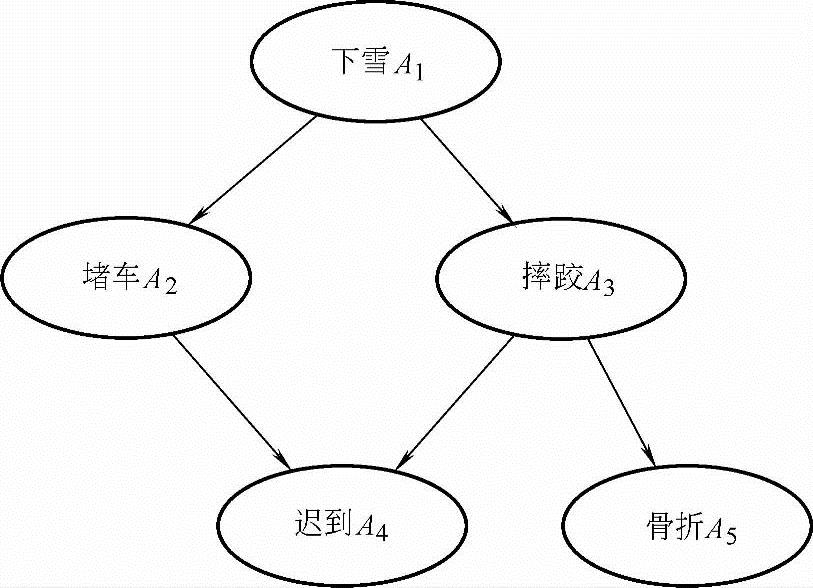
图7-4 简单的贝叶斯网络模型

下面给出关于贝叶斯网络的严格定义。

设X={X₁，X₂，…，X_n}是值域U上的n个随机变量，则值域U上的贝叶斯网络BN（Bs，Bp），其中：

1）Bs是一个定义在X上的有向无环图（DAG）г，X是该有向无环图上的节点集，E是г的边集。如果存在一条节点X_i到节点X_j的有向边，则称X_i是X_j的父节点，X_j是X_i的子节点。记X_i的所有父节点为Pa_i。

2）Bp={P（X_i|Pa_i）|X_i∈X}对于X中的每个节点，定义了一组条件概率分布函数P（X_i|Pa_i），即给定一个有向无环图г和一个离散变量集合X={x₁，…，x_n}上的联合概率分布P，如果г可以代表P，即在X中的变量和г的节点之间存在一一对应的关系，使得P可以进行如下的递归乘积分解：

式中，Pa_i是图г中X_i的父节点。将图г和概率分布P的联合称为贝叶斯网络。

2.贝叶斯网络的构建方法

以下为建立贝叶斯网络的步骤：

（1）确定为建立模型有关的变量及其解释

1）确定模型的目标，即确定问题相关的解释；

2）确定与问题有关的可能的观测值，并确定其中值得建立模型的子集；

3）将这些观测值组织成互不相容的且穷尽所有状态的变量，这样的结果不是唯一的。

（2）建立一个表示条件独立的有向无环图 根据概率乘法公式有

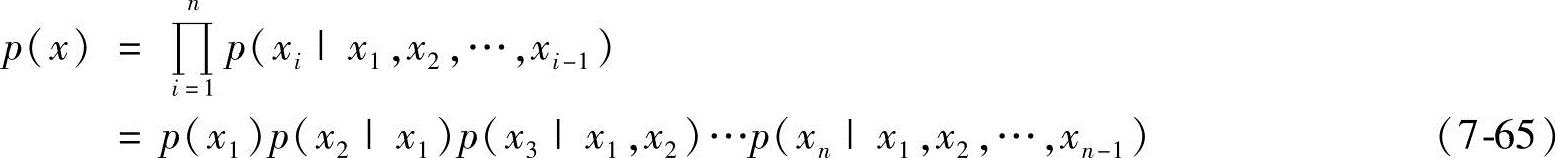
对于每个变量x_i，如果有某个子集∏_i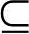{x₁，x₂，…，x_i-1}使得x_i与∏_i是条件独立的，即对任何X，有

p（x_i|x₁，x₂，…，x_i-1）=p（x_i|π_i） i=1，2，…，n （7-66）

则由式（7-65）和式（7-66）可得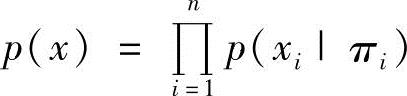。变量集合（∏₁，∏₂，…，∏_n）对应于父节点（Pa₁，Pa₂，…，Pa_n），故又可写成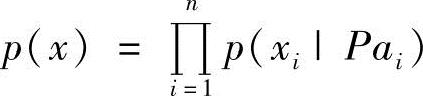。为了决定贝叶斯的结构，需要：①将变量x₁，x₂，…，x_i-1按某种次序排序；②决定满足式（7-66）的变量集∏_i（i=1，2，…，n）。从理论上说，从n个变量中找出适合条件独立的顺序，因为需要比较n！种变量顺序。因此，会造成组合爆炸问题。不过，在实际问题中，通常可以确定因果关系，且因果关系一般都对应于条件独立。所以，可以从原因变量到结果变量画一个带箭头的弧来直观地表示变量之间的因果关系。

（3）指定局部概率分布p（x_i|Pa_i） 当变量为离散变量时，需要为每个变量的父节点的各个状态指定一个概率分布。

注意，以上三步可能是交叉进行的，不是简单的顺序进行可以完成的。

构建贝叶斯网络分类器有两种方法：第一种是首先选择网络的结构，然后确定图中节点变量之间的依赖关系；第二种方法是确定特征变量的分布。特征变量可以是离散的，这种情况下的分布是概率质量函数，特征变量也可以是连续的，这种情况下就必须选择一个分布函数，常见的是高斯分布函数。这两种方法都需要确定参数集θ，因为它决定了上面决策方程所需要的分布。

贝叶斯网络学习就是寻找一个能最好匹配一个给定数据训练集的网络的过程。这个网络包含一个有向无环图（DAG）结构和与DAG中每个节点相关的条件概率表（CPT），因此贝叶斯网络学习包括学习网络结构和学习条件概率表。(www.xing528.com)

3.学习贝叶斯网络的条件概率表

通常在应用中，由领域专家给出随机变量的因果图，就可以得到贝叶斯网络结构，而要给出众多变量的CPT，对领域专家就非常难了，因此在实际应用领域中，学习CPT更具有意义。由于贝叶斯网络是变量的联合概率分布的图形表示，所以CPT学习可以归结为统计学中的参数估计问题，因此CPT学习方法可以分为两大类：基于经典统计学的学习和基于贝叶斯统计学的学习。

用于贝叶斯网络学习的样本训练集可以表达为C={C₁，C₂，…，C_m}，其中C_i={V₁=v_i1，V₂=v_i2，…，V_n=v_in}表示所有变量构成的向量{V₁，V₂，…，V_n}的实例。如果一个实例中各个变量取值确定，则称为一个完整实例，否则为不完整实例。由完整实例构成的样本训练集称为完整训练库，否则称为不完整训练库。假设变量组V={V₁，V₂，…，V_n}的联合概率分布编码于某个网络结构S中，则

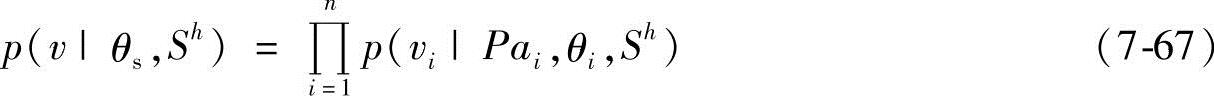
式中，θ_i为分布p（v_i|Pa_i，θ_i，S^h）的参数向量；θ_s为参数组{θ₁，θ₂，…，θ_n}的向量；S^h为联合分布可以满足网络的条件独立性假设。那么，条件概率表的学习问题就可以表示为对给定样本训练集C，计算后验分布p（θ_s|C，S^h）。

假设变量V是离散的，有r_i个可能的取值v_i¹，v²_i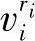，…，，每个局部分布函数是一组多项分布的集合，一个分布对应于Pa_i的一个状态，也就是假定

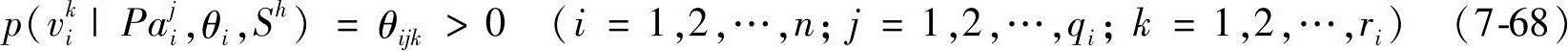
式中，Pa_i¹，Pa²_i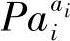，…，表示Pa_i的q_i个取值状态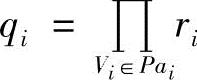，和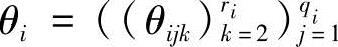是参数。θ_ijk没有列入是因为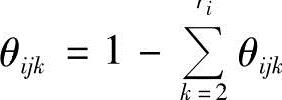。为方便起见，定义参数向量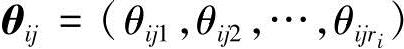。给定局部分布函数，需要有以下两个假设，才能以封闭的形式计算后验分布p（θ_s|C，S^h）：

1）样本训练集C是完整的；

2）参数向量θ_ij是相互独立的，即

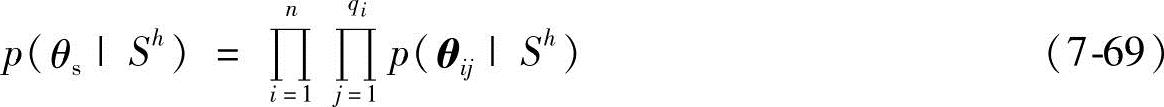
这就是参数独立假设。在以上两个假设下，对于给定的随机样本训练集C，参数仍然保持独立，即

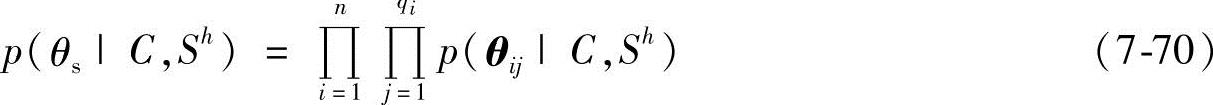
于是可以独立地更新每一个参数向量θ_ij。假设每一个参数向量θ_ij有先验Dirichlet分布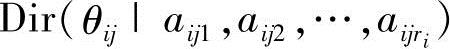，则得到后验分布为

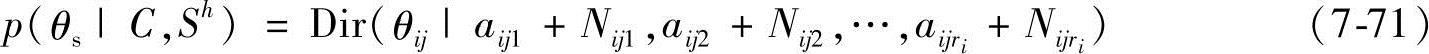
式中，N_ijk是C中V_i=v^k_i且Pa_i=Pa^j_i的样本数目。到此就获得了贝叶斯网络的条件概率参数。

当样本训练集不完整时，一般要运用近似方法，目前主要有Monte-Carlo方法、Gaussian逼近、EM（期望极大化）算法等。尽管有这些成熟的算法，但计算开销是比较大的。

4.学习贝叶斯网络的结构

当无法给出或确定贝叶斯网络的结构，而且有足够的样本数据时，需要学习贝叶斯网络结构。对于由n个变量构成的贝叶斯网络来说，由n个节点构成的所有有向无环图都可能作为贝叶斯网络的结构。Robinson于1977年发表的研究结果表明，这种结构的数目随变量数增加而指数增长，因此可能的DAG结构非常庞大。学习贝叶斯网络的结构，就是通过分析样本数据集合，从大量的结构中选出最适合的网络结构。一般需要首先定义一个关于结构的测度，再分别计算出各个可能结构的测度值，从中选取测度值最优的结构作为贝叶斯网络结构。常用的测度有两个：基于贝叶斯统计的BDE（Bayesian Dirichlet Likelihood Equivalence，贝叶斯狄利克雷似然等价）测度和基于编码理论的最小描述长度（Minimal Description Length，MDL）测度。

首先，假设网络结构是可以改进的，定义一个离散变量表示对于网络结构的不确定性，其状态对应于可能的网络结构S^h，并赋予先验概率分布p（S^h）。对于给定的样本集C，计算后验概率分布p（S^h|C）和p（θ_s|C，S^h）。其中，后者的计算方法与上节类似，前者的计算在原理上是简单的，因为

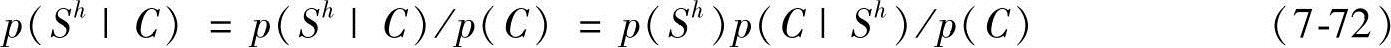
式中，p（C）是一个与结构无关的正规化常数；p（C|S^h）是边界似然。于是确定网络结构的后验分布，只需要为前一个可能的结构计算数据的边界似然。

在无约束多项分布、参数独立、采用Dirichlet先验和数据完整的前提下，参数向量θ_ij可以独立地更新。数据的边界似然正好等于每一个i-j对的边界似然的乘积：

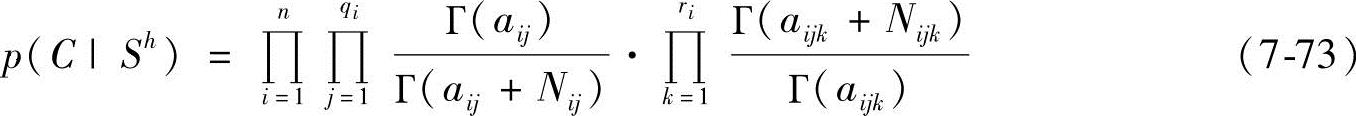
该公式首次由Cooper和Herskovits于1992年给出。

在一般情况下，n个变量的可能的网络结构数目大于以n为指数的函数。逐一排除这些假设是困难的，可以使用两个方法来处理这个问题：“模型选择”和“选择模型平均”方法。前一个方法是从所有可能的模型（结构假设）中选择一个“好的模型”，并把它当作正确的模型。后一个方法是从所有可能的模型中选择合理数目的“好模型”，并认为这些模型代表了所有情况。关于“好的模型”已有一些不同的定义和相应的计算方法（例如使用评分函数）。若干研究者的工作表明，使用贪婪搜索法选择单个好的假设通常会得到准确的预测。使用Monte-Carlo方法进行模型平均有时也很有效，甚至可以得到更好的预测。Hecherman于1995年提出，在参数独立、参数模块性、似然等价以及机制独立、部件独立等假设成立的前提下，可以将学习非因果贝叶斯网络的方法用于因果贝叶斯网络的学习。

贝叶斯网络学习的目标是，找到和样本数据匹配度最好的贝叶斯网络结构，根据观察贝叶斯网络的视角不同，还可以把贝叶斯网络结构的学习方法分成两类：基于搜索评分（Based on Scoring）的方法和基于条件独立性（Based on Conditional Independence）的方法。基于搜索评分的方法把贝叶斯网络看成是含有属性之间联合概率分布的结构，学习的目的是搜索与数据拟合最好的结构。一般的做法是给出评价网络结构的评分函数（如贝叶斯后验概率、最小描述长度和Kullback-Leiber熵等）。基于条件独立性的方法把贝叶斯网络看作是编码了变量间独立性关系的结构。学习的目的是根据独立性关系（如卡方检验）对变量分组。