Fisher线性判别方法简介

Fisher判别是一种应用得极为广泛的线性分类方法，其基本思想是：把d维空间的所有模式投影到一条过原点的直线上，即将模式的维数压缩到一维，并要求同一类型的样本尽可能聚在一起，不同类型的样本尽可能地分开。

Fisher线性判别分析（Fisher Discriminant Analysis，FDA）算法是R.A.Fisher于1936年提出的一种旨在降低特征维数的方法。FDA算法是有监督学习算法，其目标是找到线性投影方向（投影轴）使得训练样本在这些轴上的投影结果为：类内散度最小，类间散度最大。换句话说，FDA算法建立了一个子空间（由所有的投影轴构成），所有样本在这个子空间内满足类内散度最小、类间散度最大等要求。所有样本在这些投影轴上的投影系数可以作为样本的特征向量，利用这些特征向量，就可以进行样本的分类识别。

1.两类问题

先讨论简单的两类Fisher线性判别分析。

假设有一组n个d维的样本X₁，X₂，…，X_n，它们分属于两个不同的类别，其中大小为n₁的样本子集D₁属于类别ω₁，大小为n₂的样本子集D₂属于类别ω₂。如果对X中的各个成分作线性组合，就得到点积，结果是一个标量

y=W^TX （7-5）

其中，W=（w₁，w₂，…，w_n）是线性组合的权重。

这样，全部的n个样本X₁，X₂，…，X_n就产生了n个结果y₁，y₂，…，y_n，相应地属于集合Y₁，Y₂。从几何上说，如果||W||=1，那么每个y_i就是把X_i向方向为W的直线进行投影的结果，W的幅值不重要，重要的是其方向。因为，向不同方向的直线作投影，其产生的结果在可分程度上是非常不同的。如果属于类别ω₁的样本和属于类别ω₂的样本在d维空间中分别形成两个显著分开的聚类，那么希望投影后也尽量地分开。只有确定了最佳的直线方向，才能达到最好的分类效果。由此也可知道，如果各个类别的样本在原始的d维空间就是不可分的，那么无论向什么方向投影都无法产生可分的结果，因此也就不适合用线性判别分析。

下面讨论如何确定最佳的直线方向W。一个用来衡量投影结果的分量程度的度量是样本均值的差。如果u_i为第i类的d维样本均值，则有

则投影后点的样本均值为

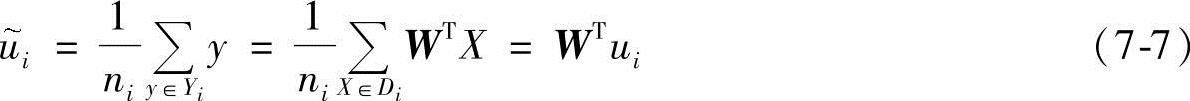
也正好是原样本均值u_i的投影，则投影后的点的两类样本均值差为

由此可见，通过改变W的幅值，可以得到任意大小的投影样本均值差。但是两类数据的投影样本均值差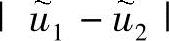的大小并不能完全体现两类数据的可分性，如图7-1所示。当投影到x轴时，投影样本均值差要大于投影到y轴的投影样本均值差，但是投影到x轴的数据可分性却明显次于投影到y轴的可分性。因此，还需要定义类内散布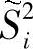。对类别ω_i的类内散布定义如下：

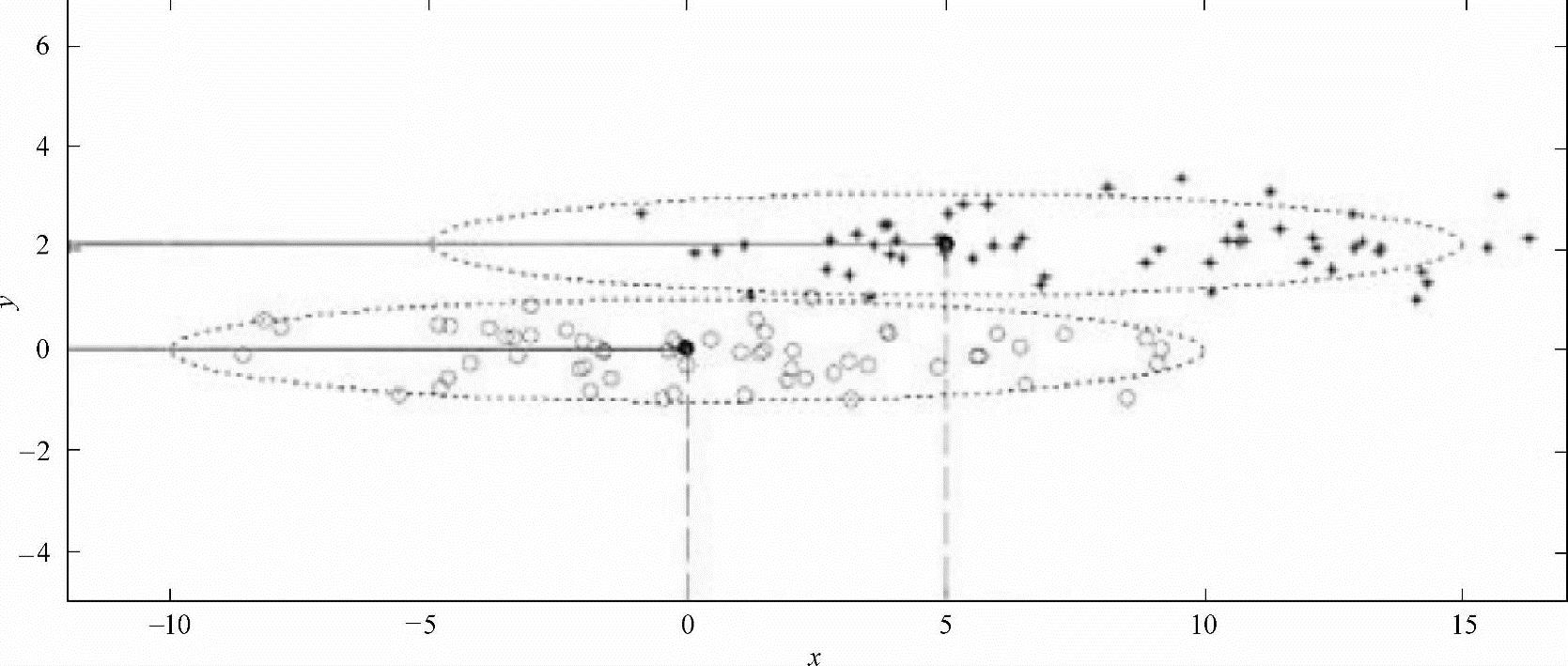
图7-1 两类数据的投影样本均值差的大小并不能完全体现两类数据的可分性

则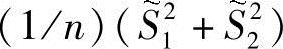就是全部数据的投影总体方差估计，而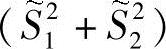称作投影样本的总类内散布。Fisher线性可分准则要求在投影y=W^TX下，要使得准则函数J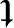（）最大化，Fisher准则函数为

为了把准则函数J（）写成W的表达式，定义了类内散布矩阵S_i和总类内散布矩阵S_W。

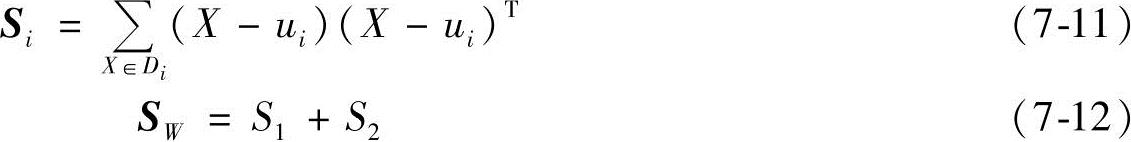
由式（7-5）、式（7-7）和式（7-9）可得

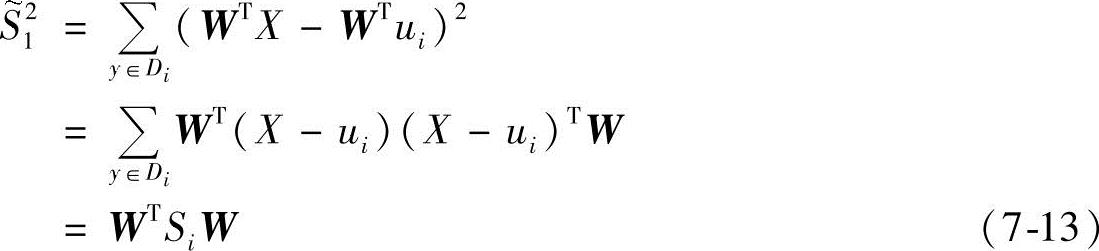
则总类内散布样本均值之差可以展开为

类似地，投影样本均值之差可以展开为

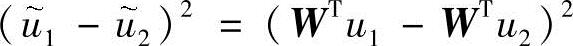
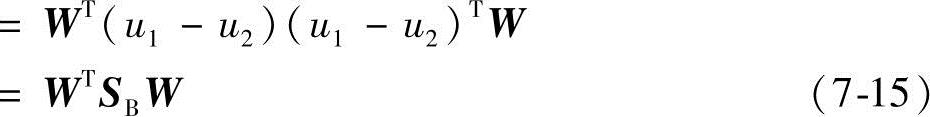
其中

S_B=（u₁-u₂）（u₁-u₂）^T （7-16）(www.xing528.com)

总类内散布矩阵S_W与全部样本的样本协方差矩阵成正比，并且是对称和半正定的。当n＞d时，S_W通常非奇异。S_B被称为是总类间散布矩阵，也是对称半正定的。此时，准则函数J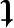（）可以写成

这个表达式在数学物理中是经常使用的，通常被称为广义的瑞利商。容易证明，使得准则函数J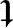（）最大化的W必须满足

S_BW=λ_iS_WW （7-18）

如果S_W是非奇异的，就能得到

S_W ^-1S_BW=λW （7-19）

此时，不需要真正地计算出S_W^-1S_B的特征值和特征向量，因为S_BW总是位于（u₁-u₂）的方向上，因此准则函数J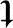（）最大时，有

W=S_W^-1（u₁-u₂） （7-20）

这个Fisher可分性判据下的W就是使得类间散布和类内散布的比值达到最大的线性函数。

这样，问题就由一个d维问题转化为一维问题。此外，真正实现分类还需要一个阈值准则来获得最终的分类器，即如何确定阈值ω₀，该阈值就是在一维空间中把两类分开的那个点。当条件概率密度函数P（x|ω_i）是多元正态函数，且各个类别的协方差矩阵Σ相同时，可以直接计算这个阈值，此时最优判决准则就是当Fisher线性判别超过阈值时，就判为属于类别ω₁，否则就判为属于类别ω₂。

2.多类问题

将两类问题的Fisher线性分析加以推广，就可以得到多类问题的Fisher线性分析。

对于c类问题，就需要c-1个判别函数。也就是说，从d维空间向c-1维空间投影，且假设d＞c。

设在n维空间R_n中给定N个样本x¹₁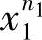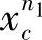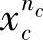，…，，…，，…，，它们分别来自c个不同的类别，其中x_jⁱ表示第i类的第j个样本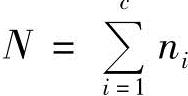，，为了衡量数据分开的程度，定义样本的类内散布矩阵S_W和类间散布矩阵S_B如下：

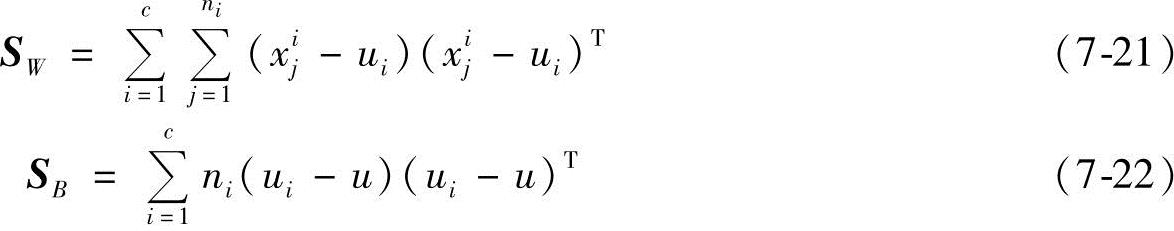
式中，c为类别数；n_i为c_i类的样本数；u_i为c_i类样本的均值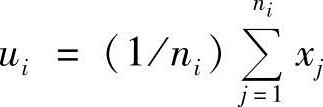，；u为所有样本的均值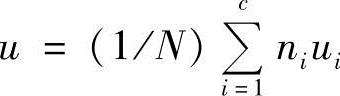，；x_jⁱ为c_i类中的第j个样本。

从d维空间向c-1维空间投影是通过下面的c-1个分类方程来进行的：

y_i=W^T_iXi=1，…，c-1 （7-23）

x₁，…，x_N投影后得到了新的样本y₁，…，y_N，这些新的样本又有自己的均值向量和散布矩阵，定义如下：

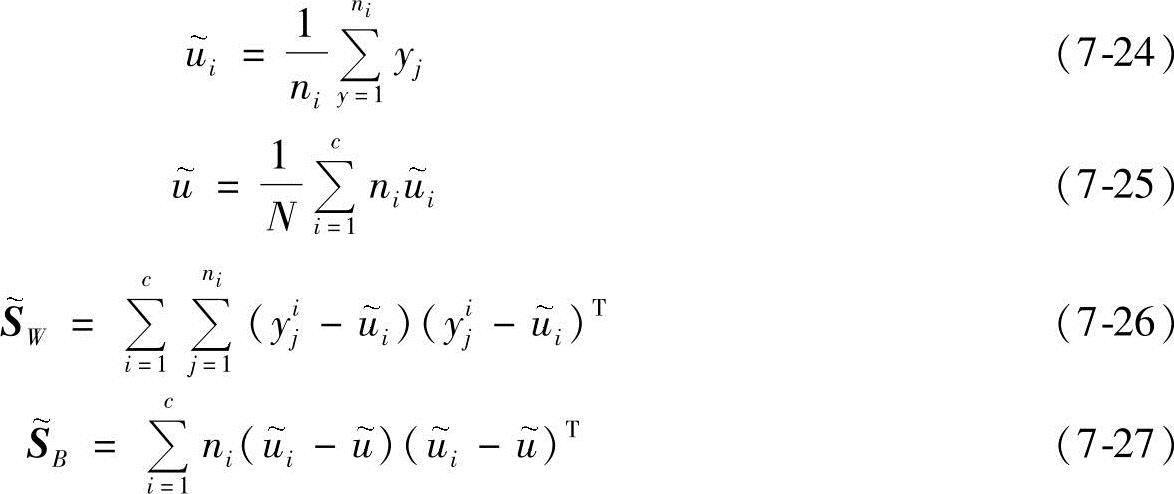
则有

我们的目的是寻找一个矩阵W，使得在某种意义上，类间离散度和类内离散度的比值最大。离散度的一种简单的标量度量是散布矩阵的行列式的值。使用这样的度量方法，得到了如下的Fisher准则函数定义为

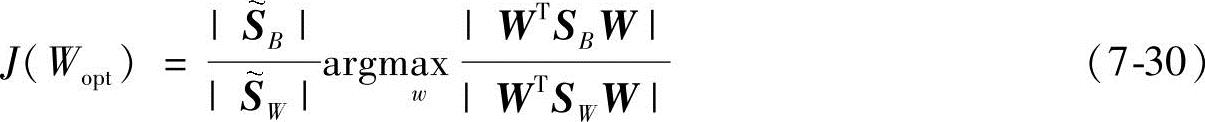
当Fisher准则函数取得最大值时，W_opt=[W₁，W₂，…，W_c-1]就是使类间离散度和类内离散度的比值最大的最优投影方向。通过求解下面广义特征方程的特征值问题就可以求出最优投影方向，[W₁，W₂，…，W_c-1]即广义特征方程的前c-1个最大特征值所对应的特征向量，即

S_BW_i=λ_iS_WW_ii=1，2，…，c-1 （7-31）

上式在S_W可逆时，即为

S_W ^-1S_BW_i=λW_ii=1，2，…，c-1 （7-32）

求出特征向量[W₁，W₂，…，W_c-1]后，就可确定式（7-23）中的c-1个判别函数，由式（7-1）可知，对于所有的i≠j有y_i（X）＞y_j（X），则把X归为ω_i类。