提取代数特征的方法及其在人脸图像中的应用

代数特征反映的是图像的一种内在属性，将图像作为矩阵看待，可对其进行各种代数变换，或进行各种矩阵分解。由于矩阵的特征向量反映的是一种代数属性，并且具有不变性，因此可用来表征图像特征。不变矩和奇异值特征是两种常用的图像代数特征，两者具有平移、尺度和旋转不变性特征，而且奇异值特征还对噪声、光照变化引起的图像灰度变化具有不敏感性。下面介绍奇异值分解（SVD）的人脸特征提取方法。

1.奇异值分解定理

二维的人脸图像相当一个高维向量，直接用其进行计算太困难，必须在保持主要特征的前提下降维，也就是希望用少量的特征来近似整个图像，而奇异值分解（SVD）就是一种实现这种效果的良好手段。

奇异值分解定理：设A是一个秩为r的n×r维矩阵，则存在两个正交矩阵

以及对角矩阵

Λ=diag[λ₀，λ₁，K，λ_r-1]∈R^n×r，且λ₀≥λ₁≥K≥λ_r-1 （6-43）

满足。式中，λ_i（i=0，1，K，r-1）为矩阵AA^T和A^TA的非零特征值；u_t和v_t分别为AA^T和A^TA和对应于λ_t的特征向量。上述分解称为矩阵A的奇异值分解，为A的λ_t奇异值。

2.基于SVD的特征提取

对于一幅大小为N₁×N₂的人脸灰度图像P（x，y），其中x∈[1，N₁]，y∈[1，N₂]，且像素值P（x，y）满足P（x，y）∈[0，1]，x为行索引值，y为列索引值，定义其投影图为

式中，V_p（x）和H_p（y）分别为图像P（x，y）的垂直和水平投影；p为平均灰度值。(www.xing528.com)

利用正面垂直人脸的对称性，对原始图像进行光照均衡处理，得到的图像为P′（x，y），如下式所示：

结合投影图后的人脸图像变为P_a（x，y），如下式所示：

用该方法处理前后的图像中光照比较均衡。另外，人脸具有多种表情，表情的变化对识别的影响也很大，而在人的五官当中，嘴巴对表情的影响最大，相比之下，眼睛和鼻子的影响相对较小。为此采用一个二值图S（x，y）叠加到人脸图像上，以进一步屏蔽嘴巴的影响，得到的图像为P_L（x，y），如下式所示：

P_L（x，y）=P_a（x，y）S（x，y） （6-47）

经过上述处理后的人脸图像不仅有效地减弱了光照的影响，同时也在一定程度上克服了表情的影响，从而较好地保留了人脸的不变性特征。令训练样本集的总体散布矩阵Σ为

式中，μ（x，y）称为平均脸，即

令矩阵W=P^TP∈R^N×N，根据奇异值分解定义，求出W的特征值λ_i和对应的正交归一特征向量V_i（i=0，1，…，N-1），再由奇异值分解定理可知，Σ的正交归一特征向量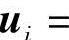，ui就是人脸图相对应特征值λ_i的特征向量，将λ_i按降序排列，并选取最大的250个特征值所对应的特征向量构成图像变换矩阵U，占有人脸特征总量90%以上，已经涵盖了人脸的主要特征。

对于任何一幅人脸图像，都可以求出其与平均脸之差在变换空间U上的投影向量P_r（x，y）=U^T[P_L（x，y）-μ（x，y）]，其中，P_r（x，y）是一个250维向量，也就是人脸图像P_L（x，y）经过特征提取后的代数特征。此时，人脸图像的维数已经大大降低，同时保留了绝大部分的有效特征信息。