离散余弦变换原理及应用分析

离散余弦变换（Discrete Cosine Transform，DCT）的变换系数是一种较好的变换系数特征。离散余弦变换的变换核为实数的余弦函数，DCT是K-L变换的最好近似，众所周知，K-L变换是基于不同的性能准则的一个最优变换。前面的PCA变换就是基于KL基的。另外，因为离散余弦变换与离散傅里叶变换很相近，所以可以对它进行有效的计算。基于这两个特性，可以用它作为人脸的特征。这里首先介绍一下离散余弦变换的理论基础。

给定长度为N的输入序列u（n），它的DCT可由下式得到：

式中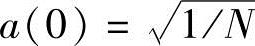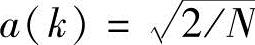，，，1≤k≤N-1。在式（6-29）中可以把u（n）序列视为一个向量U，把DCT看作一个变换矩阵，得到输出序列v（k），把v（k）序列视为一个向量V，即

V=CU （6-30）

式中，C为DCT的变换矩阵，即(www.xing528.com)

式中，k、n为变换矩阵的行和列。得到的V即为所需要的特征向量，还可以利用DCT的逆变换，将原图像进行复原，即

U=C^-1V （6-32）

式中，C^-1为C的逆矩阵。

有以上DCT的理论基础，可以看到DCT在以下几点优于PCA方法：①将每一幅图像矩阵看成一个向量，可以对每个向量进行单独处理，提取出特征向量，放入特征库里面，用于以后的识别；②当新的图像需加入库中时，经过预处理之后，可以对该图像进行DCT，无需考虑其他的图像，这样即使库中人脸图像很多时，计算量也不大，DCT的计算速度快。而PCA方法当有新的图像加入时，必须重新计算新图像与原库中所有图像的协方差矩阵，以求出新的特征空间。在第9章的人脸识别实例中，就是采用离散余弦变换系数作为HMM的观察向量来进行人脸识别的。