线性判别分析算法的优化方法

线性判别分析（LDA）算法以样本的可分性为目标，试图寻找一组线性变换，使每类的类内离散度最小，并且使类间离散度最大。经典LDA算法中使用的是Fisher准则函数，所以线性判别分析又被称为Fisher线性判别分析（Fisher LDA，FLD）。LDA也是一种很好的人脸识别的方法，但是用LDA特征提取时容易出现的问题就是小样本（SSS）的问题。这里首先对LDA的基本原理进行介绍，然后介绍其改进算法。

1.LDA基本原理

LDA选择与类内散布的正交的向量作为特征脸空间，从而能够抑制图像之间的与识别信息无关的差异，以使对光照及人脸表情变化都不太敏感。这种方法的最终目的就是找到一些特征，使得类间离散度和类内离散度的比值最大，可以较好地表现类间的差异，有利于分类。

给定属于c类的N幅人脸图像训练样本{X_i}，i=1，2，…，N，每个训练样本用一个n（=I_w×I_h）维向量表示，（I_w×I_h）为图像的大小，那么，样本的类间散布矩阵S_b，类内散布矩阵S_w可计算如下：

式中，N_i是C_i（i=1，2，…，c）类的训练样本数目；m_i为C_i类样本均值向量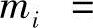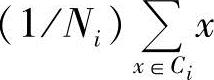，；m为所有样本的均值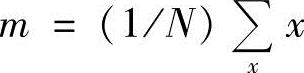，；S_i为C_i类的协方差矩阵。这时，总体散布矩阵S_t可表示为

可见S_t是所有样本的协方差矩阵。

LDA算法的目标就是找到一个最佳投影W_opt：

求解函数式（6-20）就等同于求解S_w^-1S_b的特征值问题。使J（w）最大的变化矩阵W_opt由S_w^-1S_b的前m个最大特征值所对应的特征向量组成。(www.xing528.com)

由于N不够大，引起大小为（n×n）的类内散布矩阵S_w奇异，致使S_w^-1S_b的特征值无法直接求解，这就是SSS问题。

2.LDA算法的改进

为了解决SSS问题，好多文献对此进行了研究。假定类间散布矩阵S_b和类内散布矩阵S_w的零空间分别为A和B，那么A′=Rⁿ-A和B′=Rⁿ-B分别为A和B的补空间。由Fisher准则函数可知，最优识别空间应为A′和B的交集A′∩B。

为了解决S_w的奇异问题，参考文献[4]提出了Fisherface方法。用LDA算法进行特征提取以前，先用PCA算法进行降维。该方法存在的问题是，因为PCA算法与LDA准则并不相容，虽然利用PCA算法降维使S_w满秩，但丢失了S_w的零空间，所以丢失了一部分很重要的分类信息。

另一种常用的可以解决SSS问题的方法是D-LDA（直接LDA）算法：首先去掉S_b的零空间，然后再使类内离散度最小。D-LDA算法看似避免了丢失S_w的零空间。但是，S_b和S_w的秩存在这样的关系：rankS_b≤rankS_w≤NC在去掉S_b的零空间使S_b满秩的同时，S_w也达到满秩，即采用D-LDA算法间接丢失了S_w的零空间。

还有好多解决SSS问题的方法，虽然都取得了好的结果，但是用在人脸识别上没有使人脸识别率得到提高，并且不能达到实时性的要求。

在这里只是介绍了取得好的效果和最常用的降维方法，当然还有许多其他的方法。