二维主成分分析算法简介

二维主成分分析（2DPCA）算法是一种图像特征提取方法。与PCA算法的不同之处在于，2DPCA算法是以图像矩阵为分析对象；而PCA算法是以图像的一维向量为分析对象。因此，2DPCA算法在图像特征提取之前不必降维。构造图像协方差矩阵时，2DPCA算法直接利用图像矩阵。而PCA算法首先将图像矩阵转换成列向量，然后利用列向量来构造协方差矩阵。矩阵转换成列向量的过程中，由于维数大大增高，因此进行PCA算法之前常常实施降维处理。这样的维数一般比较高，100×100的就是10000，会耗费大量的时间，并且有可能会有类内散布矩阵奇异的问题。针对这一问题，1993年Liu等人提出了一种线性鉴别分析的新思路，其基本思想是利用数字图像矩阵直接构造图像散布矩阵，并在此基础上进行鉴别分析，这就是2DPCA算法；2003年杨健等人从统计不相关性的角度，重新审视并改进了Liu的方法，从而得到一种具有统计不相关性的图像投影鉴别分析方法；2004年杨健等人将参考文献[7]所述的方法称为2DPCA方法，并将此方法用于图像重构，取得了很好的效果。下面详细讨论2DPCA算法的基本原理。

设X表示n维列向量，即X∈R^n×1。任意一副样本图像A∈R^m×n向x方向投影后，得

Y=AX （6-10）

式中，Y为样本图像A向x方向投影的特征向量，Y∈R^m×1。如何选择满意的投影方向是必须解决的问题。为此引入投影特征向量Y的总离散或协方差矩阵，通过求其迹的最大值来求最佳投影方向，其准则为

J（X）=trS_x （6-11）

式中，S_x为投影特征向量Y的协方差矩阵迹；tr（S_x）为矩阵S_x的迹。通过求式（6-11）的最大值可确定最佳投影方向x。这里

假设

G_t=E[（A-EA）^T（A-EA）] （6-13）(www.xing528.com)

式中，G_t为样本图像A的协方差矩阵。从式（6-13）可知，矩阵G_t是一个n×n维的非负矩阵，利用训练样本图像可直接求得G_t。假设训练样本数为M，A_j（j=1，2，…，M）表示第j个训练样本，且A_j∈R^m×n。矩阵G_t的计算则变为

式中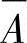，为所有训练样本的均值图像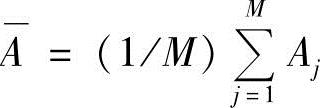，。依据式（6-12）～式（6-14），式（6-11）可转化为

J（X）=X^TG_tX（6-15）

式中，X为一维列向量，X∈R^n×1。该准则称为广义总离散度准则。当J（X）取最大值时，得到的一维列向量X叫做最佳投影轴，表明图像矩阵A向X方向投影后，投影特征向量Y的总离散度是最大的。

最佳投影轴X_opt是当目标函数J（X）取最大值时的一维向量，也就是矩阵G_t的最大特征值对应的特征向量。一般来说，只有一个最佳投影轴是不够的。通常选择d个较大特征值对应的特征向量X₁，X₂，…，X_d，这样既满足目标函数J（X）最大，又使特征向量相互正交，即

{X₁，X₂，…，X_d}=arg max J（X），且X^T_iX_j=0，i≠j，i、j=1，…，d （6-16）