图像Hough变换的原理和应用

直线y=mx+b可用极坐标表示为

r=xcosθ+ysinθ （4-54）

式中，（r，θ）定义了一个从原点到线上最近点的向量（见图4-39a），这个向量与该直线垂直。

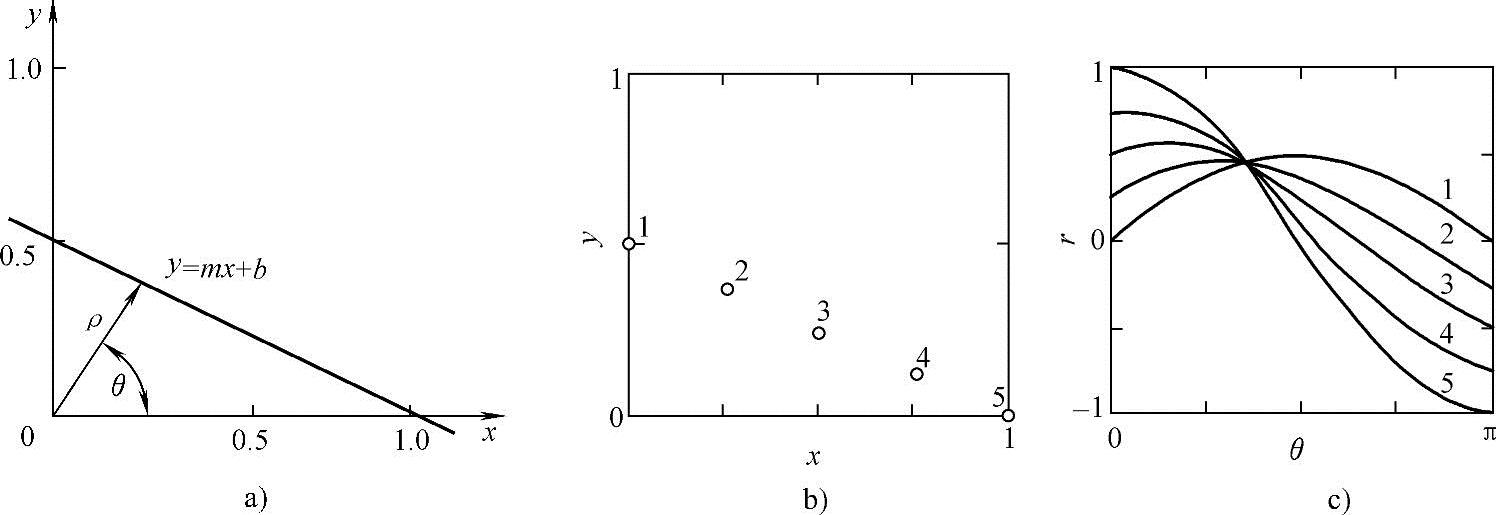
图4-39 Hough变换

a）一条直线的极坐标表示 b）x、y平面 c）r、θ平面

考虑一个以参数r和θ定义的二维空间。x、y平面的任意一直线定义了该空间的一个点。因此，x、y平面的任意一直线的Hough变换是r、θ空间的一个点。

现在考虑x、y平面的一个特定的点（x₁，y₁）。过该点的直线可以有很多条，每一条都对应了r、θ空间中的一个点。然而这些点必须是满足x₁和y₁作为常量时的等式。因此在参数空间中，与x、y空间中所有这些直线对应的点的轨迹是一条正弦曲线，而x、y平面上的任一点（见图4-39b）对应了r、θ空间的一条正弦曲线（见图4-39c）。

如果有一组位于由参数r₀和θ₀决定的直线上的边缘点，则每个边缘点对应了r、θ空间的一条正弦曲线。所有这些曲线必交于点（r₀，θ₀），因为这是它们共享的一条直线的参数。

为了找出这些点所构成的直线段，可以将r、θ空间量化成许多小格。根据每一个（x₀，y₀）点代入θ的量化值，算出各个r，所得的值（经量化）落在某个小格内，便使该小格的计数累加器加1，当全部（x，y）点变换后，对小格进行检验，有大的计数值的小格对应于共线点，其（r，θ）可用作直线拟合参数。有小的计数值的各小格一般反映非共线点，应丢弃不用。

可以看出，如果r和θ量化得过粗，则参数空间的凝聚效果较差，找不出直线的准确的r和θ值；反过来，如果r、θ量化得过细，那么计算量将增大，需要兼顾这两个方面，取合适的量化值。

若图像中各点是边沿元，而且梯度方向已求出，在寻找有无直线边沿时，可在其梯度方向内把θ精细量化，其他θ角则粗量化，这样在不增加总的量化小格数的情况下，可以提高检测直线边沿的方向角的精度。

对于圆，可写出其方程为

（x-a）²+（y-b）2=R² （4-55）(www.xing528.com)

这时参数空间增加到三维，由a、b、R组成。如果仍然像找直线那样直接计算，那么计算量和存储空间部将显著增大。

如果已知有圆的边沿元，而且边沿元为已知，那么可以简化为二维的问题。因为把上式对x取导数，有

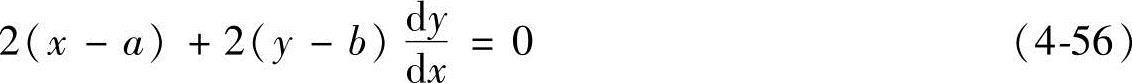
这表示参数a和b不独立，利用这个关系以后，解上式只需用两个参数（例如b和R）组成参数空间，计算量减少了很多。

在人为景物中圆形物体经常出现，经过透视成像后由圆变成椭圆。寻找椭圆的算法可以仿照寻找元的算法来进行。

设椭圆方程为

取导数有

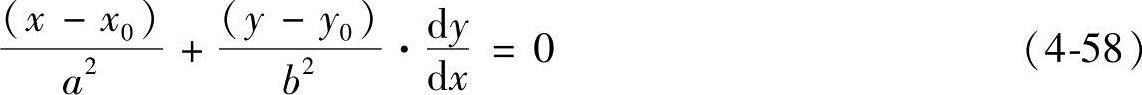
可以看到这里有三个独立参数。如果椭圆主轴不平行于坐标轴，则可写为

Ax²+Bxy+Cy²+Dx+Ey+1=0 （4-59）

在利用椭圆边沿的方向信息后，在映射空间的独立参数仍有四个之多，为了简化求椭圆的计算，还需要其他的特殊解法，这里就不多介绍了。